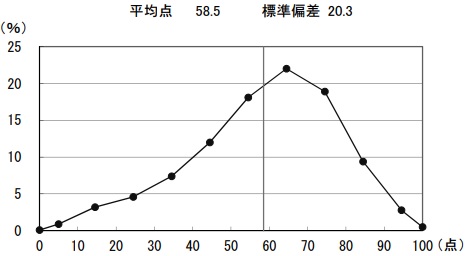
平均58.5点(前年比;+7.1点)
問題はこちら→リセマムさん
大問1(計算)-85.4%
(1) 97.7%
(-4)+(-8)
=-12
(2) 95.5%
(-3)2+12÷(-2)
=9-6
=3
(3) 72.4%
2/3(5a-3b)-3a+4b
=10/3a-2b-3a+4b
=1/3a+2b
(4) 81.7%
連立方程式:2x+3y=9・・①、y=3x+14・・②
②を①に代入する。
2x+3(3x+14)=9
2x+9x+42=9
11x=-33
x=-3
②に代入。
y=3×(-3)+14=5
x=-3 y=5
(5) 85.9%
2√27-6/√3
=2・3√3-2√3 ←有理化
=4√3
(6) 79.4%
(x+3)(x-5)+2(x+3)
(x+3)が共通するので、これをXとおくと・・
X(x-5)+2X ←共通因数Xでまとめる
=X(x-5+2) ←Xを(x+3)に戻す
=(x+3)(x-3)
大問2(小問集合)-55.9%
(1) 78.3%
反比例の比例定数aは積xy
a=3×6=18
エ
(2) 75.8%
170cm以上は、5+6+1=12人
12/30。これを百分率になおせばいい。
12×100/30=40%
(3) 40.0%
三角柱の高さは6cm。
底面積は底辺がわかっているので、あとは高さを求めればいい。
形が直角三角形なので、三平方を使用。
底面積の高さ・・√(82-62)=√28=2√7cm
三角柱の体積は、6×2√7×1/2×6=36√7cm3
(4) 47.8%
素数は、【2・3・5・7・11】(出目の和の最大が12なので11まで)
【2】・・(1,1)
【3】・・(1,2)(2,1)
【5】・・(1,4)(4,1)(2,3)(3,2)
【7】・・教科書でもやるので、6通りと暗記しちゃったほうがいい。
(1,6)(6,1)(2,5)(5,2)(3,4)(4,3) ←サイコロの対面の和
【11】・・(5,6)(6,5)
計15通り
確率は、15/36=5/12
(5) 37.4%
いつも荒ぶることで有名な千葉の作図が、今年はだいぶ大人しい設問に。
適当な正方形PBQRを書いてみて、何が使えそうかを考えてみる。
正方形の辺ではなく、対角線に着目しよう。
PやQに目がいきがちだけど、はじめに決まるのはBのはす向かいにあるR。
対角であるRは、角Bの2等分線上にある。

↑針をBにセッティングして、↑→にピョコピョコ。
そこから交差するように線を残し・・

↑R確定。これに気がつければ、正解したも同然。

↑Rを通るBCに垂直な線分。BC上にある、Qが確定する。

↑Qが確定したら、正方形の一辺は等しいので、
BQかQRの長さをとり、針をBかRにセッティングしてABとの交点をつくる。
→P確定
公式解答の2つ目は、対角線BRの垂直二等分線でPQを一気に求めている。
理由は、正方形の対角線は垂直かつ二等分で交わるから。
大問3(関数)-39.8%
(1) 85.5%
A(1、2)
これをy=ax2に代入する。
a=2
(2)① 27.9%!
CDは平行四辺形の一辺なので、平行四辺形の4つの頂点の座標に狙いを定める。
直線OBは原点を通る比例。
A(1、2)で、OA:OB=1:4ということは、
Bの座標はAの座標の4倍→B(4、8)
直線mはx軸と平行なので、Cのy座標も8
Cのx座標は・・8=2・x2 x=±2
Cのx座標は負なので、x<0 x=-2 →C(-2、8)
Dも次の問題で使うので求めておく。
BCの距離が6だから、ODの距離も6→D(-6、0)
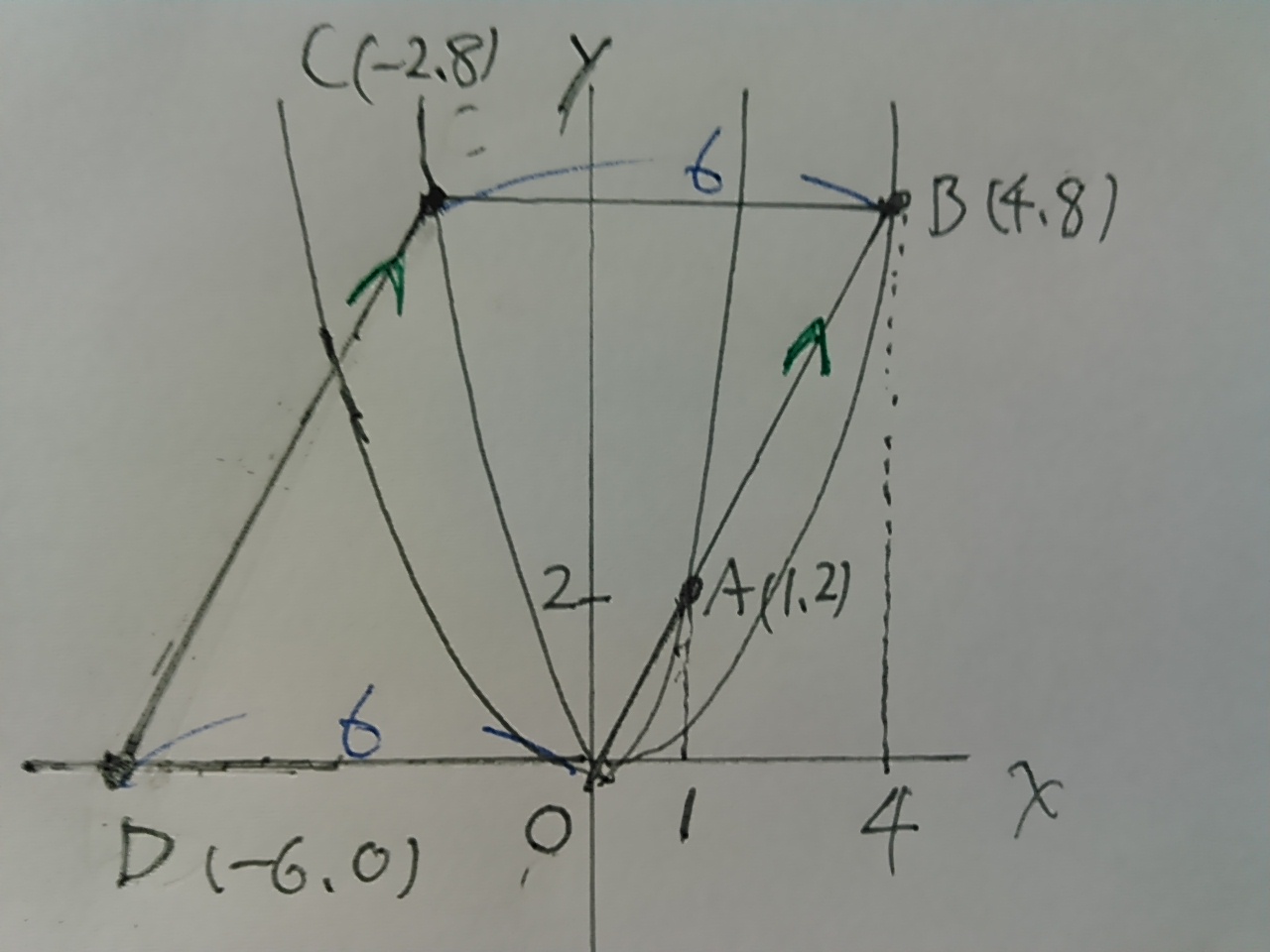
OBとDCは平行だから、傾きも一緒。
OBの傾き→OAの傾き→右に1、上に2だから、傾き2
DCの傾きは2
一次関数:y=ax+bの式をCかDの座標に放り込み、切片bを求める。
以下、Dに代入。
0=2×(-6)+b
b=12
直線CDの式は、y=2x+12
(2)② 6.1%!!
平行四辺形OBCDをピックアップ。

OA:AB=①:③とおく。
対辺のDCは④となる。
平行四辺形OBCDの面積は□8、台形OAPDの面積を□3とおくと、
残りの台形ABCPの面積は□5となる。
台形同士の面積比は【上底+下底】
(平行線は高さが同じで、上と下の辺の合計値が台形の面積比となるから)
これを利用すると・・
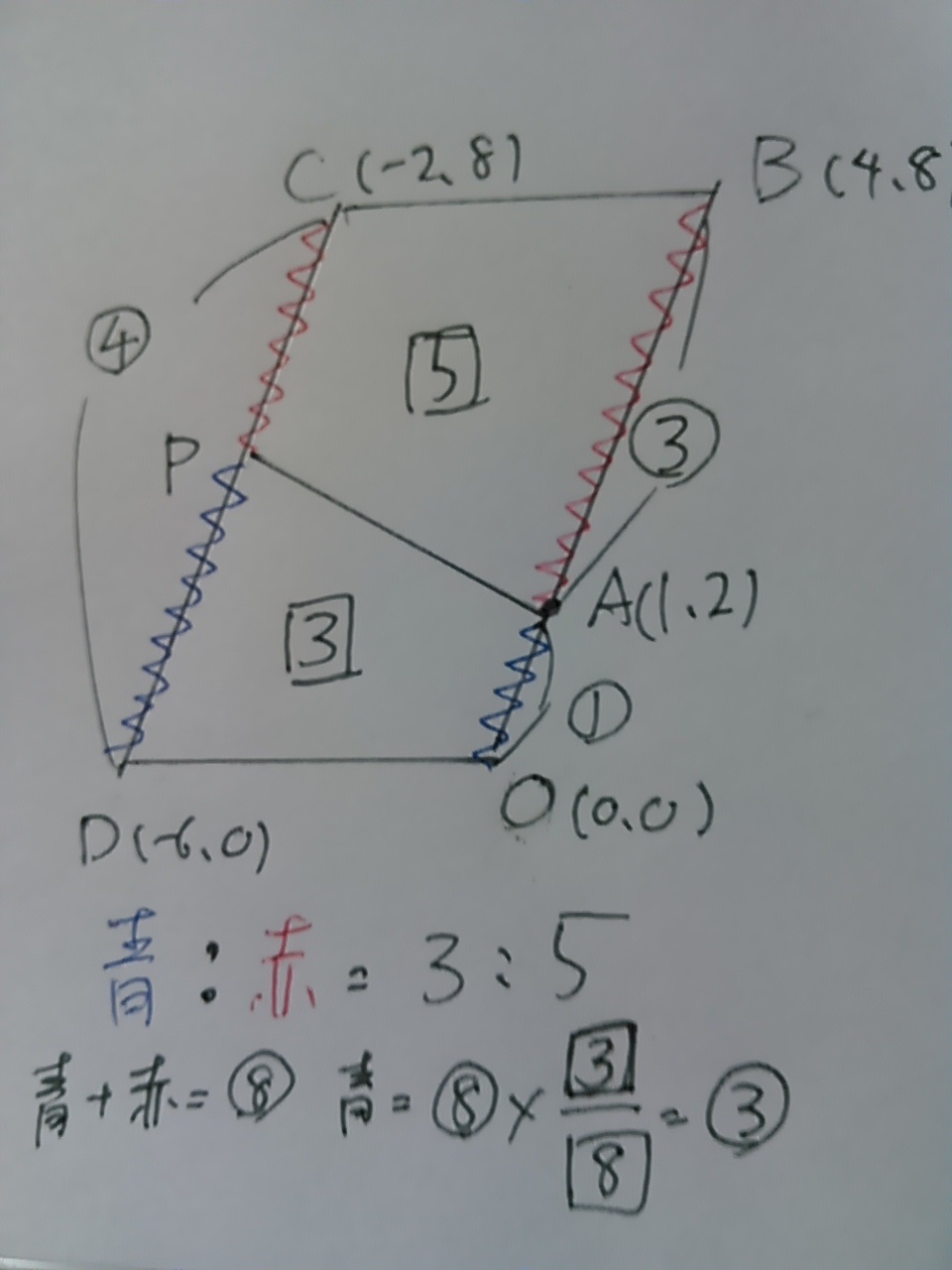
青の両側の和:赤の両側の和=3:5
赤青の両側(対辺の全体)が⑧なので、
青の両側の和は、⑧×3/8=③
つまり、青のOA+DP=③
OA=①だから、DP=③-①=②
PC=DC-DP=④-②=②
DP:PC=②:②=1:1となり、PがDCの中点であることがわかる。
DとCの座標から、P(-4、4)となる。
青の左側DPが○のいくつかを知るには、青の右側OAが①とわかっているので、
【青の左側+右側の合計が○のいくつか】を知ればいい。
右と左の和を一体として捉える。ここで、台形の面積比を用いる。
大問4(平面図形)-45.1%
(1)誘導に従う。
a・・∠BADと∠ECDの関係 → 錯角 ア 85.2%
b・・∠ADBと対頂角にある角 → ∠CDE カ 96.8%
c:証明の完成。6点-23.1%! 3点-11.4% 無答-33.4%
△BEFが二等辺三角形であることを証明したい。
思いつきやすいのは、2辺か、2つの底角のいずれが等しいこと。
とりあえず、等しいところに記号がふってみる。
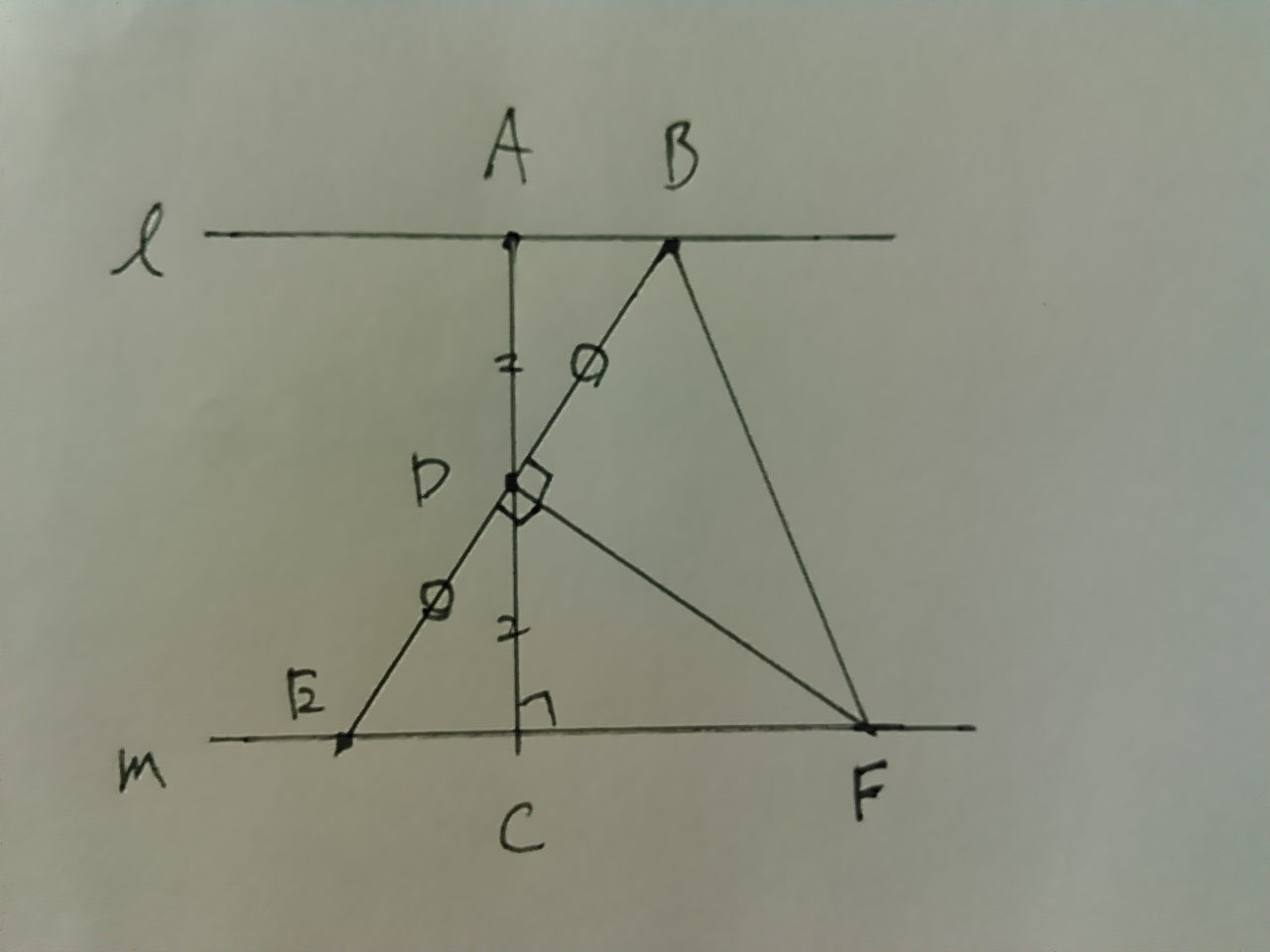
↑FB=FEか、∠FBD=∠FEDのどちらかを説明したい。
いずれにせよ、△BDFと△EDFの要素なので、
△BDF≡△EDFであることを示せばよい。
道筋は立てやすいでしょう。
BD=ED、共通辺DF、その間が直角→2辺と間の角が等しい。
△BDF≡△EDF → 辺か底角が等しいことを述べる。
(2) 6.0%!!
円がないのに、円の半径を求めさせる。

ここで、おや?っと気付く。
線分ACからの距離がBとGで等しい。
つまり、GはBの真下にある。
BGをつなげる。
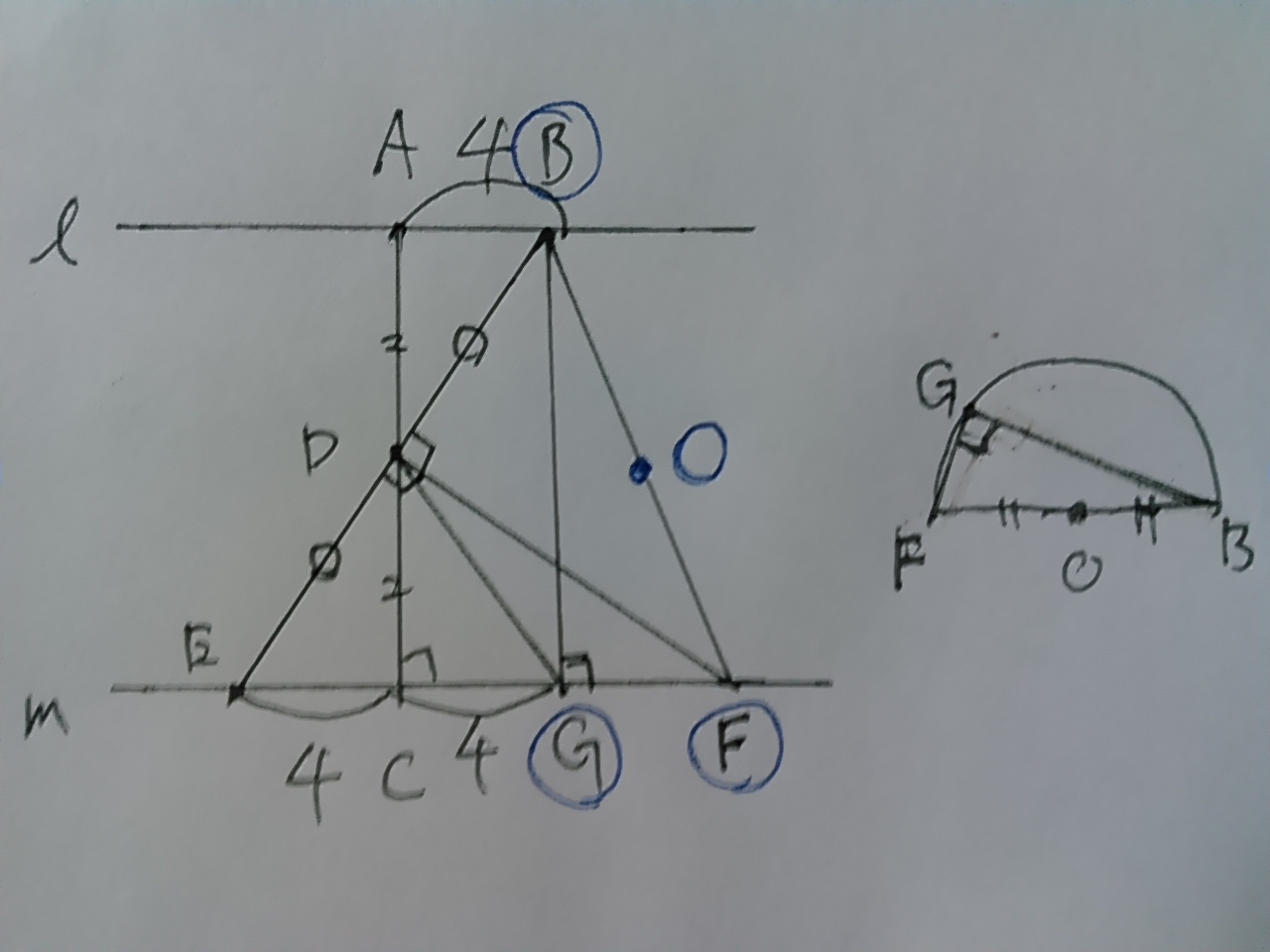
∠BGF=90°
これはありがたい。
”直角三角形の斜辺の中点は、3つの頂点を通る円の中心点”なので、
3点BFGを通る円の中心は、BFの中点にくるとわかる。
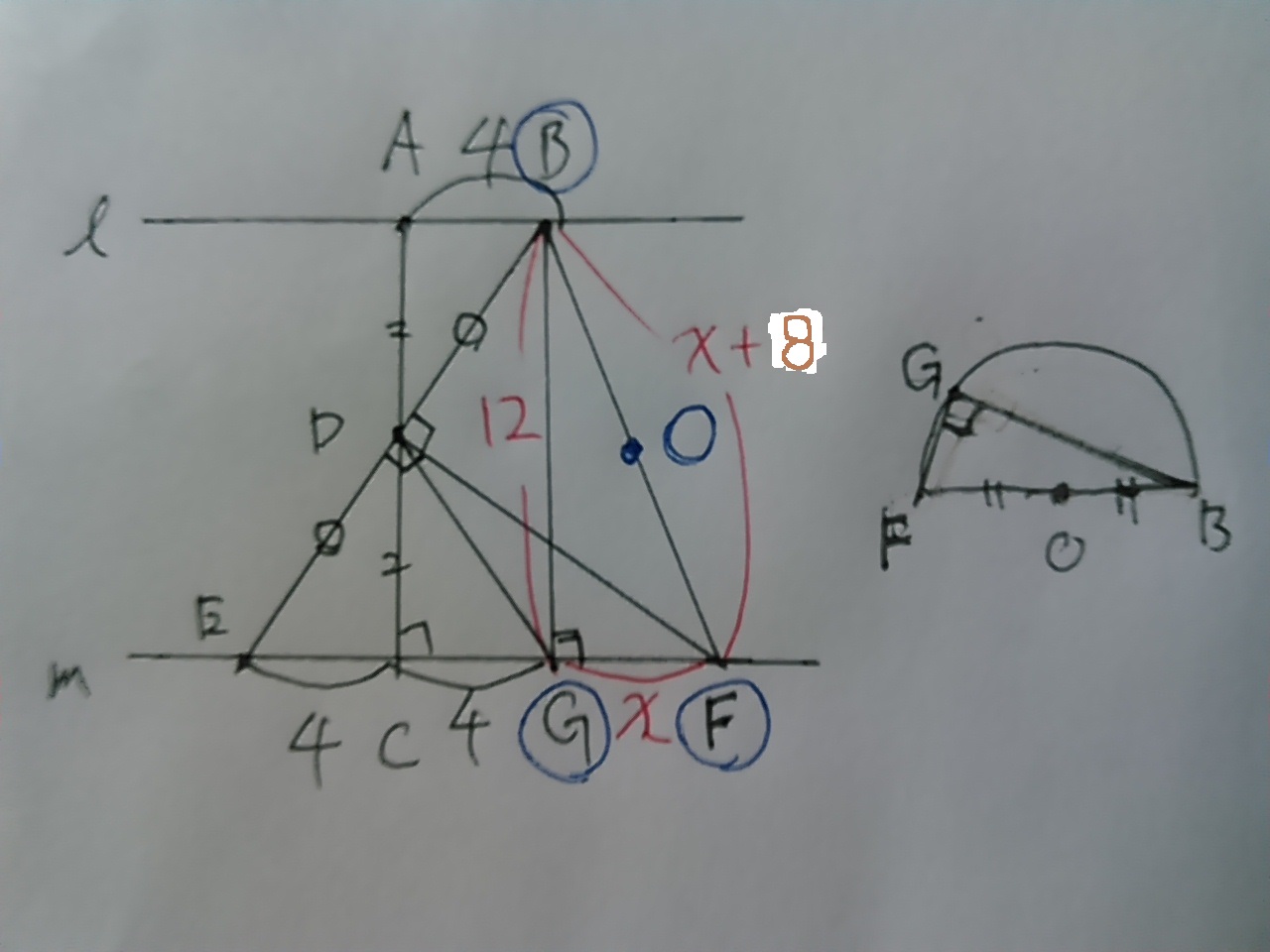
直径のBFを知りたい。
GFをxとおく。
△BEFは二等辺→FE=FBより、FB=x+8
△BGFで三平方。
(x+8)2=122+x 2
x2+16x+64=x2+144
16x=80
x=5
BF=5+8=13
半径OB=13/2cm
@別解@
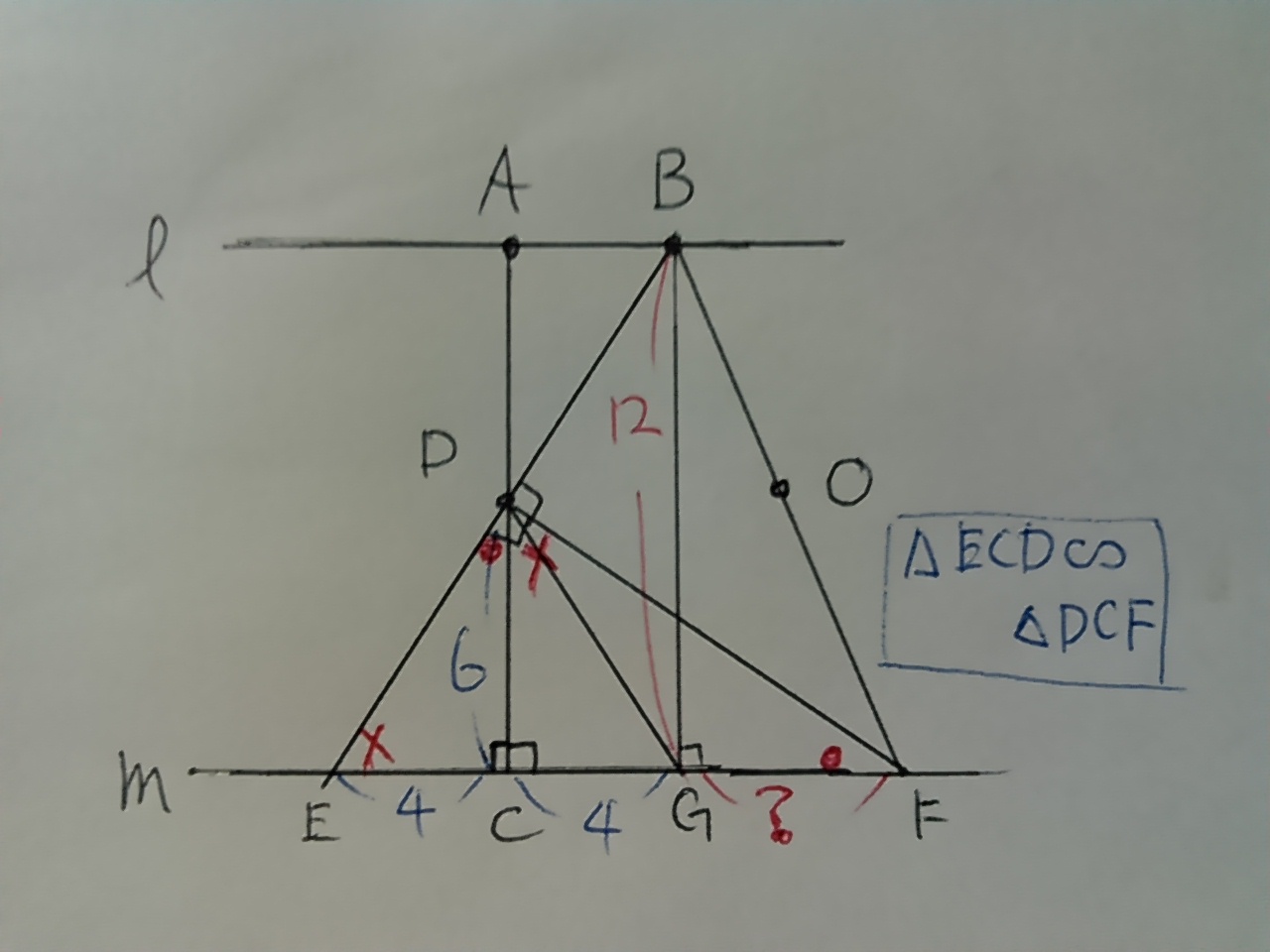
GFの長さは相似でも求めることができる。
直角三角形DEF内で、等しい角度に印をつける。
●+×=90なので、△ECDと△DCFは2角が等しく相似。
EC:CD=DC:CF=4:6
CF=6×6/4=9cm
GF=9-4=5cm
△BGFは5:12:13の直角三角形となる。→BF=13cm
直角三角形は相似の宝庫!
大問5(規則)-61.0%
問題がシンプルなので、とっつきやすい。
(1)
青→白の順に増えていく。
ア・・9 95.7% イ・・12 93.3%
(2) 74.7%
7番目まで埋めてみる。

青は【1、1、4、4、9、9、16・・】
平方数が2連続する。2つの平方数を〔1セット〕と考える。
青が36枚なので、36=6×6 (青の枚数=セット数×セット数)
つまり、6セット目に入ったときに青がはじめて36枚となる。
5セット+1をすればいい。
2×5+1=11番目
12番目は36の2回目。題意に適さない。
1つの違いが命取り。
(3) 34.9%
総枚数の規則。
【1、3、6、10、15・・】
連続する整数枚を紙の下に並べていくので、+1、+2、+3・・
(表より図2をみた方がわかりやすい)
n番目の総枚数は、nまでの総和となる。
30番目は、1~30までの和。
(1+30)×30×1/2=465枚
(4) 6.3%!!
総枚数が1275枚となったときをn番目とおく。
前問と同様。(1+n)×n×1/2=1275
n2+n-2550=0
nの係数が1で2550の符号が負であるから、
(n+〇)(n-△)=0で、〇と△の差は1である。
2550を素因数分解すると、2×5×5×51
51が曲者なので、【2×5×5、51】→【50、51】と処理できる。
n2+n-2550=0
(n+51)(n-50)=0
n>0ゆえ、n=50
50番目までの白紙の枚数を求める。
青の方がわかりやすい規則なので、
総枚数から青をひいて白を出す。
50番目まで平方数の組が、50÷2=25セット
50番目までの青の枚数は、25×25=625枚 (青の枚数=セット数×セット数)
白の枚数は、1275-625=650枚
n2+n-2550=0の因数分解には、やや計算力が問われる。
素因数分解で大きな素数が現れたら、それを除け者にしてみよう。



コメント