大問1(計算)
(1)
7-(-5)
=7+5
=12
(2)
(-4)2+3×(-2)
=16-6
=10
(3)
3/2x-6y-1/4(3x-8y)
=3/2x-6y-3/4x+2y ←後半の符号注意
=3/4x-4y
(4)
2:5=(x-2):(x+7)
内項の積を外項の積が一緒であることから、
5(x-2)=2(x+7)
5x-10=2x+14
3x=24
x=8
(5)
√45-√20+15/√5
=3√5-2√5+3√5 ←√5に統一
=4√5
(6)
(x+1)(x-7)-20
=x2-6x-7-20
=x2-6x-27
=(x-9)(x+3)
大問2(小問集合)
(1)
文字式。問題文から、a=7b+3
これをbについて解く。
7b=a-3
b=(a-3)/7
エ
(2)
BCとCDに補助線をひく。

(弧CD=弧DE)
図形が円に囲まれている→円周角定理
円周角の定理から、弧BCに対して∠BAC=∠BDC=24°
弧CD=弧DEから、CD=DE→△DECは二等辺三角形
∠CED=DCE=38°
△CDFより、180-(38+24)=118°
(3)
@通常の平均計算@
A~Eの身長を求める。
A=160+8=168
B=160-2=158
C=160+5=165
D=160
E=160+2=162
6人の身長の総和は、161.5×6=969
969-(168+158+166+160+162)
=969-813=156cm
@仮の平均を用いる方法@
仮の平均を160とおく。
6人の身長の平均は仮の平均より、161.5-160=+1.5
身長の総和は、仮の身長で計算するときより、+1.5×6=+9になる。
Fの身長をxとおくと、
+8-2+5+0+2+x=+9
x=-4
160-4=156cm
(4)
球が登場。
球の体積は、4/3πr3
4/3×3×3×3×π=36πcm3・・・円柱の体積
4×4×π=16πcm2・・・円柱の底面積
円柱の高さは、36π/16π=9/4cm
(5)
@情報の整理@
白=大きいサイコロ 左周りに進む
黒=小さいサイコロ 左から☆型に進む
白(大きいサイコロの目)を基準に場合分け。
(白、黒)=(大、小)=(1、3)(2、1)(2、6)(3、4)(4、2)(5、5)(6、3)
計7通り
*2の目のときだけ2つある。
大小サイコロ全ての出目パターンは、6×6=36通り
確率は、7/36
(6)
恒例の作図問題。ヒネリがあって難しい。
2点A、Bから等距離=ABの垂直二等分線上に点Pがある。

Aからヒョコ。
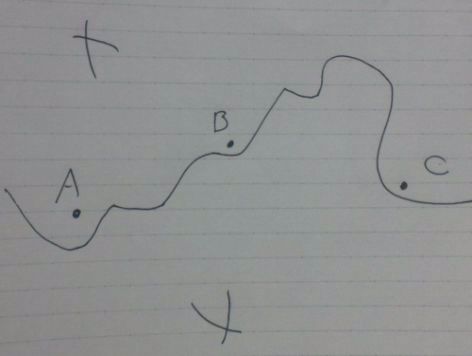
同じ長さでBからヒョコ。
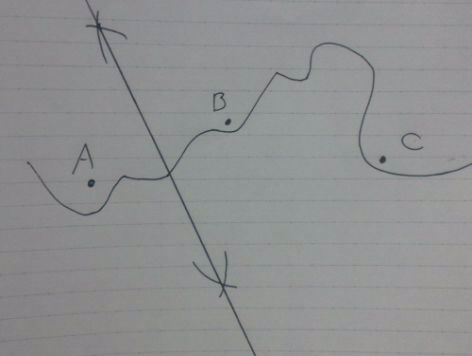
この線上のどこかにPがある。
ここからが本題。
∠BPCが30°となるようなPの位置を確定したい。
30°といえば、正三角形や直角三角形を思い浮かぶが、
点Pの位置が不明なので、∠BPCを直接、描くのが難しい。
そこで、円周角の定理を使う。
中心角60度であれば、円周角はどこも30°であることを利用する。

この円周上のどこかに点Pがある。
△OBCは、OB=OCで∠BOC=60°すなわち正三角形となる。
BCを1辺とする正三角形を作図する。

BからCとの距離をとってヒョコ。
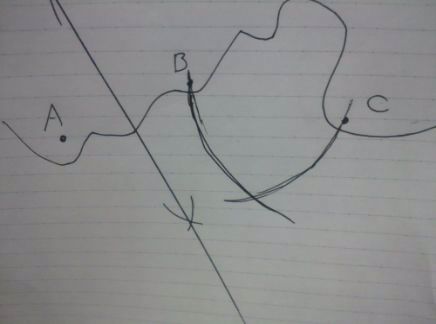
同じ長さでCからヒョコ。

目分量で書いたのでかなりいびつな正三角形に・・。
交点が円の中心になる。
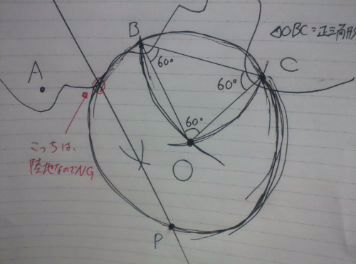
半径OB,OCとなるよう、グルッと円を書く。
さきほどの垂直二等分線と交わる点がPとなる。
ただし、上の交点は陸地なので船が通れない×。
大問3(関数)
(1)
AC=BCということは、△ABCは点Cを頂角とした二等辺三角形。

Cのx座標は2
点A、B、Cの座標をすべて求める。
A(4、4) B(0、4) C(2、1)
△ABCは底辺が4で高さが3
4×3÷2=6cm2
(2)
この手の問題は、座標を文字に置き換える。
x座標、y座標の値がともに小さいCのx座標をaとおく。

点C(a、a2/4)
点Aのx座標は点Cのx座標の2倍なので、A(2a、a2)
ここで、△ABCをピックアップ。

正方形を描くと、ABは正方形の対角線、ABと点Cとの距離は対角線の半分。
3/4・a2×2=2a
3/2・a2=2a
3a2=4a
3a=4
a=4/3 ・・・Cのx座標
点Aのx座標は2aなので、8/3
A(8/3、16/9)
大問4(方程式・規則)
あまり見かけないパターンの文章問題。文字式を使って、丁寧に長さを判定していく。
(1)
対角線×対角線÷2=正方形の面積
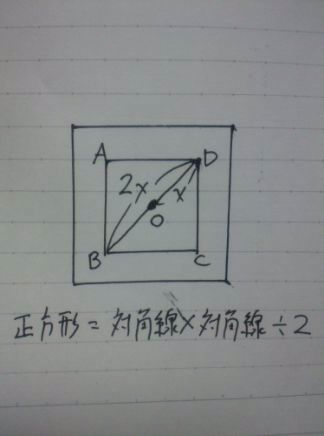
対角線BD=2xより、
y=2x×2x÷2=2x2
中の正方形は、{2(x-2)}2÷2=(2x-4)2÷2=2x2-8x+8
外の正方形は、(1)より、2x2
y=2x2-(2x2-8x+8)=8x-8
(3)(a)
【1】は2秒周期、【2】と【3】は3秒周期、【4】は4秒周期。
2と3と4の最小公倍数12秒後まで調べる。(2<x≦3を3秒後と考えてしまう)
| 1秒後 | 2秒後 | 3秒後 | 4秒後 | 5秒後 | 6秒後 | 7秒後 | 8秒後 | 9秒後 | 10秒後 | 11秒後 | 12秒後 | |
| 【1】 | ○ | × | ○ | × | ○ | × | ○ | × | ○ | × | ○ | × |
| 【2】 | ○ | × | × | ○ | × | × | ○ | × | × | ○ | × | × |
| 【3】 | ○ | ○ | × | ○ | ○ | × | ○ | × | × | ○ | × | × |
| 【4】 | ○ | ○ | × | × | ○ | ○ | × | × | ○ | ○ | × | × |
以後、12秒間で上の規則が繰り返される。
次に全てつくのは、2周期目のはじめ、つまり13秒後まで(12<x≦13)
ア・・12 イ・・13
(b)
101÷12=8…5
101秒は、8周期+5秒
つまり、上の周期表の5番目が、101秒後の状況。
点灯するのは【1】、【3】、【4】
大問5(平面図形)
(1)
(a)【1】は正三角形の説明。
正三角形の1辺であり、△ACFの1辺でもあるACが答え。
ア
(b)
説明から∠BCA=∠ACD=∠DCF=60°
∠BCEに対応する角は∠ACFも120°となる。
オ
(c)
前問がわかれば明白。
(2)
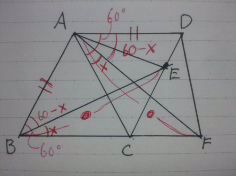
△ABE≡△DAFを証明したい。
正三角形の1辺からAB=DA
誘導で求めた△BCE≡△ACFを利用して、BE=AF
これらの間の角である∠ABE=∠DAFを証明すればよい。
△BCE≡△ACFから、∠EBC=∠FAC=∠×をすれば、
∠ABE=60-×、∠DAF=60-×で、∠ABE=∠DAFとなる。
2辺と間の角が同じとなり、2つの三角形は合同となる。
以下、模範解答の例。
~引用はじめ~
△ABEと△DAFにおいて、
仮定から、AB=DA ・・・【6】
【】5より、 BE=AF ・・・【7】
∠CBE=∠CAF・・・【8】
また、∠ABE=∠ABC-∠CBE
=60°-∠CBE ・・・【9】
∠DAF=∠DAC-∠CAF
=60°-∠CAF ・・・【10】
【8】、【9】、【10】より、∠ABE=∠DAF・・・【11】
【6】、【7】、【8】より、2辺とその間の角がそれぞれ等しいので、
△ABE≡△DAF
~引用おわり~
(3)
相似やDFの長さに目を向けてしまいそうだが、
△ACD内を三平方の定理でいじくれば求められる。

△ACDは1辺10cmの正三角形。
CE:ED=3:2から、CE=6cm、ED=4cm
AからCDに垂線をひき、その交点をGとする。
正三角形を縦にわると、1:2:√3の直角三角形。
△AGEで三平方の定理 を使用する。
AE2=(5√3)2+12=76
AE>0から、AE=√76=2√19cm




コメント