2023年度　三重県公立高校入試問題過去問・後期選抜【数学】解説

平均27.2点（前年比：－0.3点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
４－（－３）
＝４＋３
＝７

（２）
６（２ｘ－５ｙ）
＝12ｘ－30ｙ

（３）
５/√５＋√20
＝√５＋２√５
＝３√５

（４）
ｘ²－５ｘ＋４
＝（ｘ－１）（ｘ－４）

（５）
３ｘ²－７ｘ＋１＝０
解の公式を用いて、ｘ＝（７±√37）/６

（６）

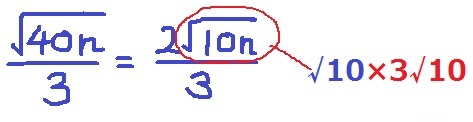
√（40ｎ）＝２√（10ｎ）
√（10ｎ）の根号を外すには、ｎに√10を含ませる。
また、分母の３を約分する必要があるので、かけあわせるべき最小数は３√10＝√90。
ｎ＝90

（７）
ｙ＝ａｘに（ｘ、ｙ）＝（10、－２）を代入。
－２＝10ａ
ａ＝－１/５

ｙ＝－１/５ｘにｙ＝２/３を代入。
２/３＝－１/５ｘ
ｘ＝－10/３

（８）

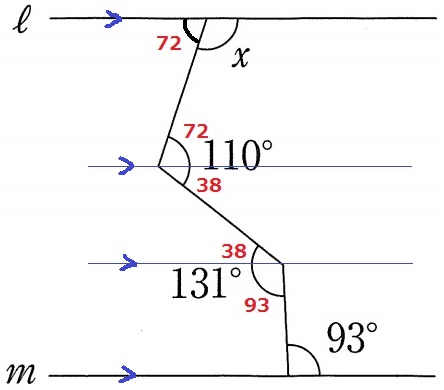
平行線をひき、錯角を連鎖していく。
131－93＝38°
110－38＝72°
ｘ＝180－72＝108°

（９）

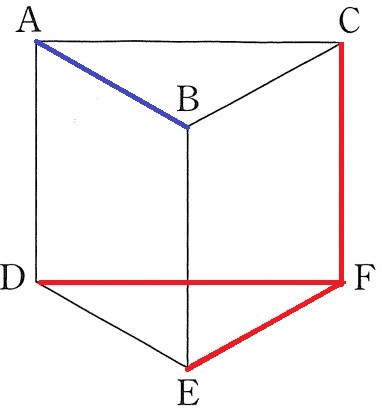
ネジレの位置→延長しても交わらない、かつ平行でもない。
ＢＣとＣＡ、ＡＤ、ＢＥは、ＡかＢを含むのでＡＢと交わる。×
ＤＥはＡＢと平行。
残りのＣＦ、ＥＦ、ＦＤがネジレ。
オ・キ・ク

（10）
最頻値（モード）…最もあらわれている値。
４～６秒の階級値である５秒。

（11）

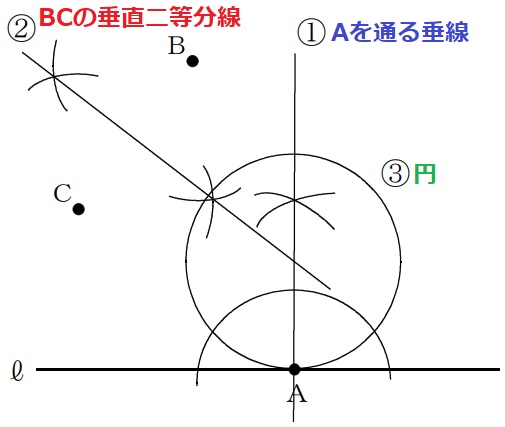
①『直線ℓと点Ａで接する円』→Ａを通る直線ℓに対する垂線。
②『２点Ｂ、Ｃから等距離にある円』→ＢＣの垂直二等分線。
③うえの交点を中心とする円。半径は中心とＡとの長さ。

大問２（データの活用）

（１）
第１四分位数は箱の左端。
６点

（２）
Ｂの最小値３、第１四分位数13、中央値16、第３四分位数17、最大値19。
最小値がまだ登場していないので、ｍ＝３
昇順に並べ替えると、【３、12、14、15、17、17、19】と未知数ｎ。
８人の第１四分位数は下から２番目と３番目の平均13。
中央値は４番目と５番目の平均16。
第３四分位数は上から２番目と３番目の平均17。
・・どれも合っている(‘Д’)
下の方にｎをいれると１個ずつズレてしまうので上の方に入れる。
ｎ＝17であれば、第３四分位数も崩れない。
ｍ＝３、ｎ＝17

（３）

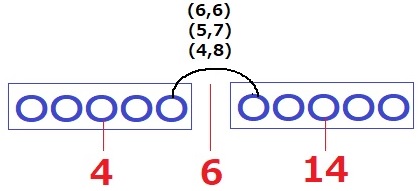
10人の第１四分位数は３番目、中央値は５番目と６番目の平均、第３四分位数は８番目。
５番目の６番目の平均が６となる組み合わせは、（６、６）（５、７）（４、８）。
しかし、（３、９）だと５番目の値が４未満となり、３番目の第１四分位数と合わなくなる。
よって、６番目の値は６か７か８。

（４）①
範囲＝最大値－最小値
Ａは18－２＝16点、Ｂは19－３＝16点で同じ。〇
ア

②
Ｃの上から３番目は14点であるが、ＡとＢは不明。
（Ａの第３四分位数14点は上から２番目と３番目の平均）
ウ

大問３（方程式）

（１）
120人は小中学生の合計。
ｘ＋ｙ＝120
30人は100ｍ走の参加者の合計。
35/100ｘ＋20/100ｙ＝30
①…ｘ＋ｙ、②…35/100ｘ＋20/100ｙ

（２）
先の連立を解く。
ｘ＋ｙ＝120　…①
35/100ｘ＋20/100ｙ＝30　←100倍
35ｘ＋20ｙ＝3000　←÷５
７ｘ＋４ｙ＝600　…②

②－①×４で、３ｘ＝120
ｘ＝40
①に代入、ｙ＝80
小学生…40人、中学生…80人

大問４（確率）

（１）
【のぞみ】グ、グ、チョ、パ
【けいた】グ、チョ、チョ、パ
全体の取り出し方は、４×４＝16通り
けいたが勝つパターンは、グが１通り、チョが１×２＝２通り、パが２通り。
計５通りだから、確率は５/16。

（２）
【のぞみ】グ、グ、チョ、パ
【けんた】グ、チョ、チョ、チョ
のぞみが勝つパターンは、グが３×２＝６通り、チョが０通り、パーが１通り、計７通り。
けんたが勝つパターンは、グが１通り、チョが１×３＝３通り、計４通り。
のぞみの勝ちがけんたより３通り多い。

けんたにパを１枚追加するたびに、勝つパターンはのぞみが＋１通り、けんたが＋２通り。
→けんたの勝ちがのぞみより１通り多くなる。
３÷１＝３枚のパーを追加すると勝ちパターンが同じ⇒勝つ確率が等しくなる。
ａ＝３

大問５（関数）

（１）
ｙ＝１/４ｘ²にｘ＝２を代入→ｙ＝１
Ｂ（２、１）

（２）
同様にＡ座標を求めると、Ａ（－６、９）
Ａ（－６，９）→Ｂ（２、１）
右に８、下に８だから、傾きは－１。
Ｂから左に２、上に２移動して、切片は１＋２＝３
ｙ＝－ｘ＋３
ａ＝－１、ｂ＝３

（３）

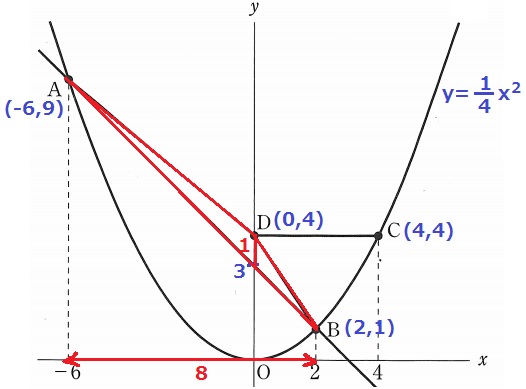
ｙ＝１/４ｘ²にｘ＝４を代入→Ｃ（４、４）だからＤ（０、４）
ＡＢの切片が３なので、△ＡＢＤは底辺が１、高さの合計が８の三角形。
１×８÷２＝４ｃｍ²

（４）

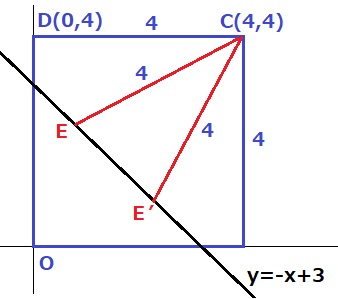
ＣＤ＝ＣＥ＝４
Ｃから４離れる直線上のＥは２ヶ所ある。
グラフ上の点座標を求める問題は、２つのグラフの交点から方程式を立てるのが定石だが、
Ｅは放物線上の点ではない(´･_･`)
Ｃ座標から青い四角形は１辺４の正方形である。これをうまく使えないか。

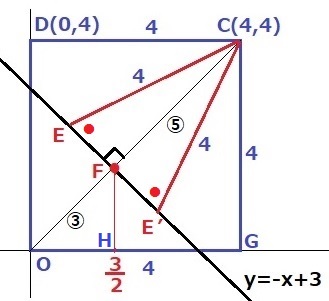
対角線ＯＣに補助線。
ＯＣ（ｙ＝ｘ）とｙ＝－ｘ＋３は傾きの積が－１だから直交する。
交点をＦとするとＦのｘ座標は、
ｘ＝－ｘ＋３
ｘ＝３/２

ＯＣは正方形の対角線で４√２。
Ｃ、Ｆの真下の点をそれぞれＧ、Ｈとする。
△ＦＯＨ∽△ＣＯＧから、ＯＦ：ＯＣ＝３/２：４＝③：⑧
ＦＣ＝４√２×⑤/⑧＝５√２/２

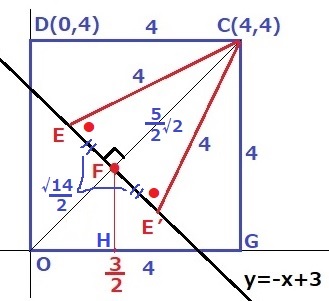
△ＣＥＦで三平方→ＥＦ＝√14/２
傾き－１から１/√２倍すると、ＥとＦのｘ座標の差は√７/２である。
△ＣＥＥ’は二等辺三角形でＣＦを対称の軸として線対称。
ＥＦ＝Ｅ’Ｆより、ＥとＥ’のｘ座標はＦから±√７/２なので、
ｘ＝（３±√７）/２

＠別解＠

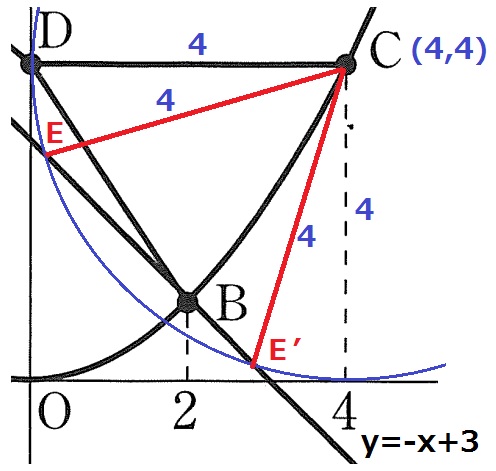
Ｅ、Ｅ’はＣを中心とする半径４の円周上にある。

高校数学の基本問題より。
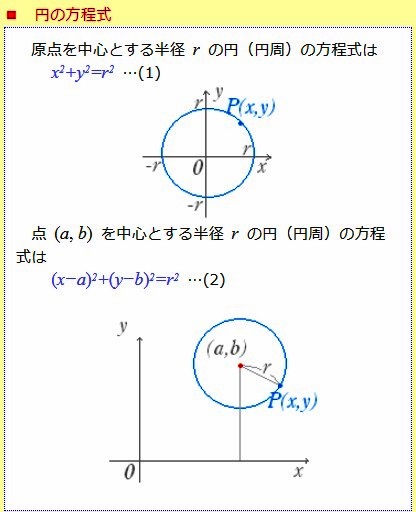
高校２年生で扱う内容ですが、円の方程式というものがあります。
原点を中心とする半径ｒの円を式で表すと、ｘ²＋ｙ²＝ｒ²
中心が（ａ、ｂ）にあると、（ｘ－ａ）²＋（ｙ－ｂ）²＝ｒ²が成り立ちます。

中心Ｃ（４、４）、半径ｒ＝４の円の方程式は、
（ｘ－４）²＋（ｙ－４）²＝４²
円と直線との共有点は、２直線の交点が方程式の解で求まるのと同じです。
ｙ＝－ｘ＋３を代入して、
（ｘ－４）²＋（－ｘ＋３－４）²＝16
（ｘ－４）²＋（－ｘ－１）²＝16　←（－ｘ－１）²＝－（ｘ＋１）・－（ｘ＋１）＝（ｘ＋１）²
（ｘ－４）²＋（ｘ＋１）²－16＝０
２ｘ²－６ｘ＋１＝０
解の公式を適用して、ｘ＝（３±√７）/２

大問６（平面図形）

（１）
△ＡＢＤ∽△ＤＡＦの証明。

ＡＢ//ＦＧの錯角（×）。
仮定の角の二等分線と弧ＣＥに対する円周角（●）。
２角相等で∽。

（２）①

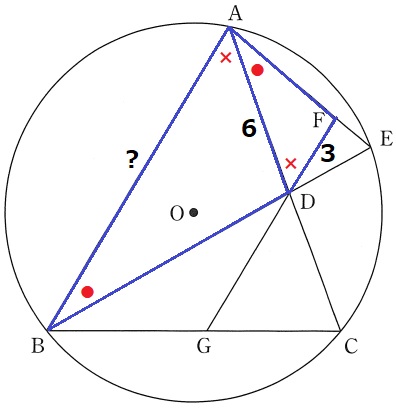
先の∽を用いる。
△ＡＢＤ∽△ＤＡＦより、ＡＢ：ＡＤ＝ＤＡ：ＤＦ＝２：１
ＡＢ＝６×２＝12ｃｍ

②

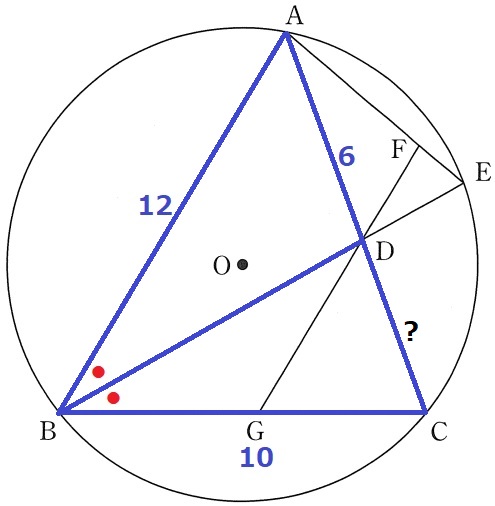
角の二等分線の定理から、ＢＡ：ＢＣ＝ＡＤ：ＤＣ＝６：５
ＡＤ＝６ｃｍなので、ＤＣ＝５ｃｍ

△ＡＢＣ∽△ＤＧＣより、ＡＢ：ＤＧ＝ＡＣ：ＤＣ＝⑪：⑤
ＤＧ＝12×⑤/⑪＝60/11ｃｍ

大問７（空間図形）

（１）
円錐の高さは、三平方を用いて√（12²－４²）＝８√２ｃｍ
体積は、４×４×π×８√２÷３＝128√２/３πｃｍ³

（２）

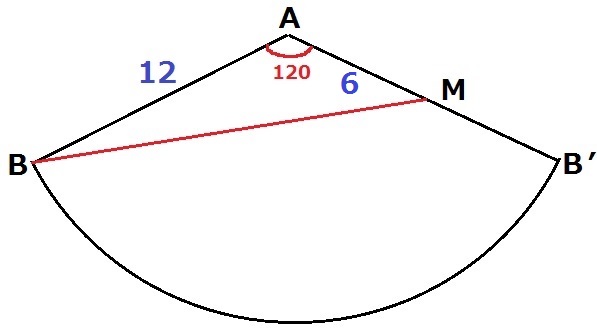
最短距離の問題なので展開図を作成。
側面積の扇形の中心角は、360×半径/母線＝360×４/12＝120°

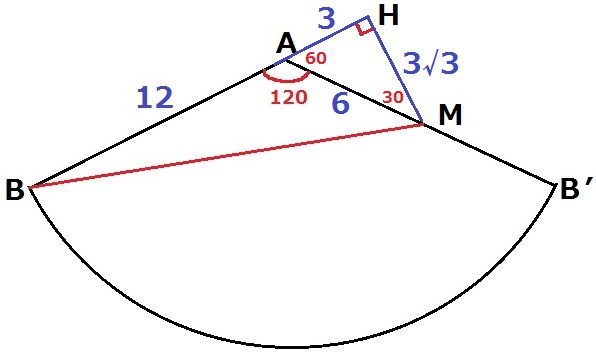
ＢＡの延長とＭを通る垂線の交点をＨとする。
△ＡＭＨは有名三角形で辺の比は１：２：√３→ＡＨ＝３ｃｍ、ＭＨ＝３√３ｃｍ
△ＢＭＨで三平方→ＢＭ＝６√７ｃｍ