2022年度　山梨県公立高校入試問題過去問【数学】解説

平均54.8点（前年比；－4.3点）
最高点―100点、最低点―０点

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）　99％
４－12
＝－８

（２）　89％
４/５÷（－４）＋８/５
＝－１/５＋８/５
＝７/５

（３）　95％
（－６）²－３²
＝36－９
＝27

（４）　92％
７√３－９/√３
＝７√３－３√３
＝４√３

（５）　81％
１/６ｘｙ×（－18ｘ）
＝－３ｘ²ｙ

（６）　93％
７（２ｘ－ｙ）－（ｘ－５ｙ）
＝14ｘ－７ｙ－ｘ＋５ｙ
＝13ｘ－２ｙ

大問２（小問集合）

（１）　80％
２ｘ²＋９ｘ＋８＝０
解の公式を適用して、ｘ＝（－９±√17）/４

（２）　65％
円周角は中心角の半分。
ｘ＝232÷２＝116°

（３）　71％

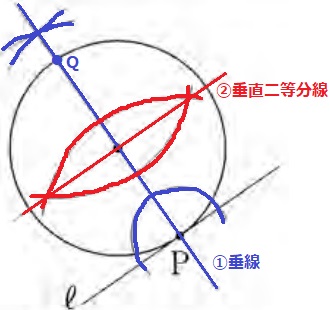
半径と接線は直交する。Ｐを通る垂線上に円の中心がある。
反対側の円周上の交点をQとする。
ＰＱが円の直径で、この中点が円の中心。
①垂線と②垂直二等分線の交点が答えになる。

（４）　60％
ア：ｙ＝１/５ｘ
イ：ｙ＝50/ｘ（反比例）
ウ：ｙ＝３ｘ
エ：ｙ＝0.8ｘ
イ
*イ以外は比例。

（５）　66％（部分点１％）
全体は、６×６＝36通り
10の倍数ごとで場合分け。
積が10→（２、５）（５、２）
積が20→（４、５）（５、４）
積が30→（５、６）（６、５）
もう無い。計６通り。
確率は、６/36＝１/６

大問３（整数&数量変化）

（１）①　77％
与式にｘ＝12を代入する。
６×12－２（20－12）
＝72－16＝56点

②　26％！（部分点11％）

確かにいずれも８の倍数…。
式を変形して、８（　　）の形にもっていく。

６ｘ－２（20－ｘ）
＝８ｘ－40
＝８（ｘ－５）
ｘ－５は整数だから、８（ｘ－５）は８の倍数である。
したがって、最終億点は８の倍数になる。

（２）①　54％

ＰはＡＢの中点。
△ＰＢＣの面積は△ＡＢＣの半分なので、
８×６÷２÷２＝12ｃｍ²
*誤答では16、20が見られた。

②　44％

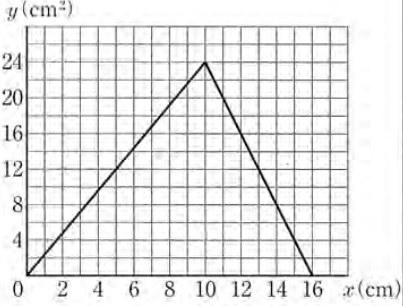
０≦ｘ≦10では高さが長くなる→面積は一次関数（比例）で増加。
ｘ＝10のとき、△ＰＢＣの面積は△ＡＢＣと同じ24ｃｍ²
10≦ｘ≦16では高さが短くなる→面積は一次関数で減少。
ｘ＝16のとき、△ＰＢＣは０ｃｍ²
原点→（10、24）→（16、０）を結ぶ。

③　19％！（部分点23％）

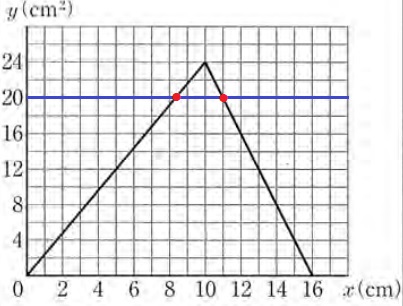
先ほどのグラフでｙ＝20との交点のｘ座標が答え。
後半は右に１、下に２の傾きで格子点を通過しているので、ｘ＝11
前半をどうするか。。

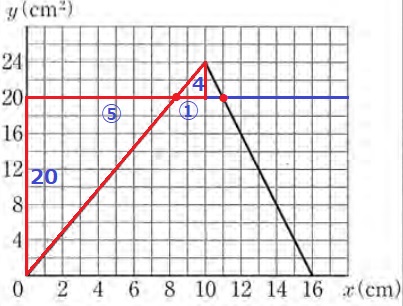
上のような三角形の相似に着目する。
10ｃｍ＝⑥なので、10×⑤/⑥＝25/３
ｘ＝25/３、11

大問４（データの活用）

（１）①　79％

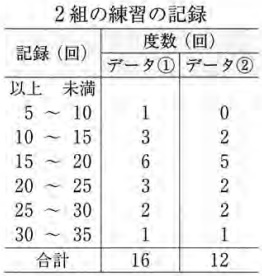
５以上～10未満、10以上～15未満…
階級の幅は５回。

②　38％
効率良く比較しないと時間がとられる。
５～10のデータ②は０なので×。
25～30と30～35は度数が同数なので、分母の小さいデータ②が大きい。

10～15と20～25はデータ①とデータ②の度数が同じ。
３/16と２/12＝１/６を最小公倍数48で通分すると、９/48＞８/48
データ①が大きい。
15～20は、６/16＝３/８と５/12を比較。９/24＜10/24
データ②が大きい。
ウ・オ・カ

（２）①　データ①…85％、データ②…83％

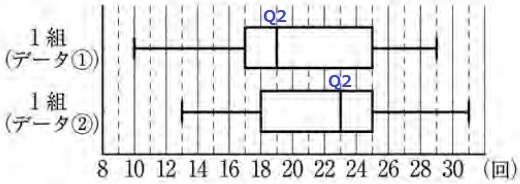
第２四分位数（Ｑ2）が中央値（メジアン）。
データ①…19回、データ②…23回

②　27％！（部分点37％）
説明問題。

最大値は同じ。
箱の横の長さ（四分位範囲；Ｑ3－Ｑ1）はデータ①が８、データ②が７でほぼ同じ。
箱全体が右側に寄っているデータ②の方がデータ①より記録が伸びている。
*正解に至らない例として、「すべての四分位数にふれて説明していない、
中央値のみで２つの箱ひげ図を比較、①の箱ひげ図と②の箱ひげ図が比較されていない」。
採点上の注意にあるように、②の箱が①の箱より右にある（ａ）でも正答なので、
”すべての四分位数に触れる”は（ｂ）の方と思われる。

大問５（関数&平面図形）

（１）①　78％
ｘ＝０のとき、最小値ｙ＝０
ｘ＝６のとき、最大値ｙ＝12
０≦ｙ≦12

②　64％
ｙ＝１/３ｘ²にｘ＝－３、９を代入して、
Ａ（－３、３）⇒Ｃ（９、27）
右に12、上に24だから、傾きは24/12＝２
Ａから右に３、上に６移動して、切片は３＋６＝９
ｙ＝２ｘ＋９

③　15％！

Ｂの真上にあり、ＡＣとの交点をＤとする。
ＡＣの傾きは２なので、Ｃから左に３、下に６移動してＤ（６、21）

ＡとＣを通るｙ軸に平行な線で△ＡＢＣを等積変形。
すると、底辺はＡとＣのｘ座標の差12、高さはＢとＤのｙ座標の差９となる。
12×９÷２＝54

（２）①　19％！（部分点52％）
△ＡＢＥ∽△ＥＣＦの証明。

よくあるタイプである。
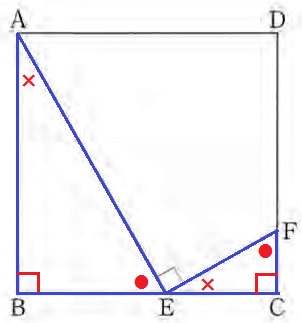
●＋×＝90°の角度調査。２角相等で∽。
記述の仕方は公式解答を参照してください。

②　５％!!

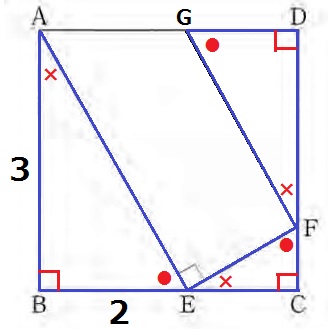
●＋×＝90°を進めて、△ＡＢＥ∽△ＥＣＦ∽△ＦＤＧ。

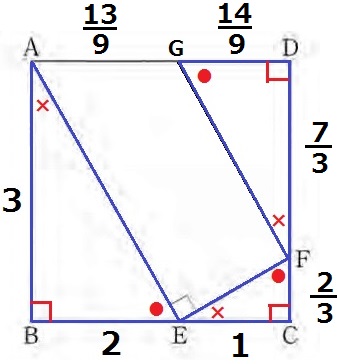
３：２を反時計回りに適用していく。
ＥＣ＝３－２＝１ｃｍ
ＣＦ＝１×２/３＝２/３ｃｍ
ＦＤ＝３－２/３＝７/３ｃｍ
ＤＧ＝７/３×２/３＝14/９ｃｍ
ＡＧ＝３－14/９＝13/９ｃｍ
ＡＧ：ＧＤ＝13/９：14/９＝13：14

大問６（空間図形）

（１）　68％（部分点１％）
△ＥＰＱは等辺が９ｃｍの直角二等辺三角形。
辺の比は１：１：√２だから、ＰＱ＝９√２ｃｍ

（２）ＡＥＰＱ…34％、ＲＦＰＳ…26％！
三角錘Ａ―ＥＰＱの体積は、９×９÷２×６÷３＝81ｃｍ³

△ＡＢＲ∽△ＰＦＲより、相似比はＡＢ：ＰＦ＝６：３＝２：１
ＲＦ＝６×１/３＝２ｃｍ

△ＦＰＳ∽△ＥＰＱで、△ＥＰＱが直角二等辺だから△ＦＰＳも同様。
ＦＳ＝ＦＰ＝３ｃｍ
三角錐Ｒ—ＦＰＳの体積は、３×３÷２×２÷３＝３ｃｍ³

（３）　１％!!!
難易度上昇:( ´ω` ):

体積から五角形ＡＲＳＵＴを出そうとすると、高さを求めるのが大変な気がする(;`ω´)
立体全体が左右対称で、△ＡＰＱは二等辺三角形。
△ＡＢＲ∽△ＰＦＲの相似比が②：①で、△ＰＦＲ≡△ＳＦＲだから、
△ＡＢＲと△ＳＦＲの相似比も②：①。
右側の△ＡＤＴと△ＵＨＴについても同様のことがいえる。

ＲＳとＴＵを延長した交点をＶとする。
ＳとＵがそれぞれＦＧとＨＧの中点であることから、ＲＳ＝ＳＶ＝ＴＵ＝ＵＶ
四角形ＡＲＶＴは１辺が②の菱形。
これをうえのように８等分してみると、△ＲＰＳと△ＴＵＱと合同の三角形で分割できる。

底辺ＲＴが２で割り切れるので、二等辺三角形ＡＲＴに注目する。
ＲＴは等辺６ｃｍの直角二等辺の斜辺だから６√２ｃｍ。
△ＡＢＲで三平方→ＡＲ＝√52ｃｍ
△ＡＲＴの左半分で三平方→高さは√34ｃｍ
△ＡＲＴの面積を７/４倍すれば五角形ＡＲＳＵＴがでる。
６√２×√34÷２×７/４＝21√17/２ｃｍ²

（４）　２％!!

求積すべき立体は四面体（三角錐）である。
面倒臭そうだが、変形するとスッキリと求められる。

ＡＣの中点をＷ、ＲとＴと同じ高さにあるＡとＣの真下をそれぞれＸ、Ｙとする。
面ＷＲＴとＡＸ、ＣＹが平行であることに注目し、等積変形でＡをＸに、ＣをＹに移す。
すると、立体は正四角錘Ｗ―ＸＲＹＴに変形できる。
６×６×４÷３＝48ｃｍ³