2022年度　千葉県公立高校入試【思考力を問う問題】解説

問題はコチラ→ＰＤＦファイル
３教科60分試験100点満点

大問１（数学）

（１）
Ｐ―Ｑ間は時速５ｋｍ、Ｑ―Ｒ間は時速４ｃｍ。
両区間は距離が等しく、仮にそれぞれを最小公倍数20ｋｍとすると、
Ｐ―Ｑ間は４時間、Ｑ―Ｒ間は５時間で合計９時間。
（平均の速さ）＝（合計の距離）÷（合計の時間）
40ｋｍ÷９時間＝時速40/９ｋｍ

（２）

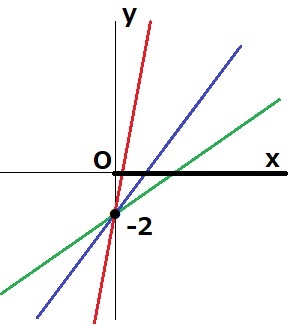
直線ｙ＝（６/７－ｂ/ａ）ｘ－２
一見、複雑な式だが、この直線がｘ軸と正の部分で交わるということは、
とどのつまり、傾きの（６/７－ｂ/ａ）が正になるでお終い(;^ω^)

６ａ＞７ｂが成り立つ（ａ、ｂ）の組み合わせを調べる。
●ａ＝１　→　なし
●ａ＝２　→　ｂ＝１
●ａ＝３　→　ｂ＝１～２
●ａ＝４　→　ｂ＝１～３
●ａ＝５　→　ｂ＝１～４
●ａ＝６　→　ｂ＝１～５
以上、15通り。
全体は６×６＝36通りなので、確率は15/36＝５/12

（３）①

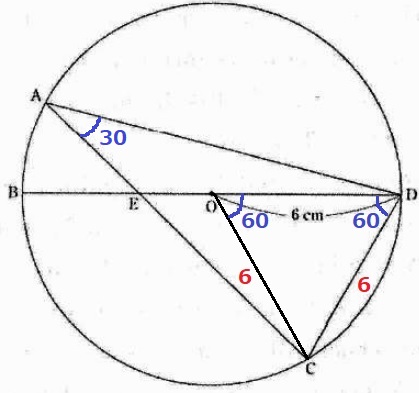
半径と仮定から、△ＯＣＤは１辺６ｃｍの正三角形。
∠ＣＯＤ＝∠ＯＤＣ＝60°
弧ＣＤの円周角より、∠ＣＡＤ＝60÷２＝30°

△ＡＣＤは二等辺だから、∠ＡＣＤ＝（180－30）÷２＝75°
最後に△ＥＣＤで外角定理を使う。
∠ＢＥＣ＝75＋60＝135°

②

前問の∠ＢＥＣ＝135°から、∠ＣＥＤ＝180－135＝45°
有名角が出てくるので、有名三角形をつくる。
ＣからＢＤに垂線、交点をＨとすると、△ＣＨＤは１：２：√３の直角三角形、
△ＣＨＤは直角二等辺三角形になる。

ＨＤ＝６×１/２＝３ｃｍ
ＢＨ＝直径ＢＤ－ＨＤ＝９ｃｍ
ＥＨ＝ＣＨ＝６×√３/２＝３√３ｃｍ
よって、ＢＥ＝ＢＨ－ＥＨ＝９－３√３ｃｍ

（４）①
Ｄはｙ＝ｘ²上の点でｘ＞０、ｙ＝９→Ｄ（３、９）
原点ＯからＤまでは右に３、上に９だから、傾きは９÷３＝３
平行である直線ℓの傾きも３である。

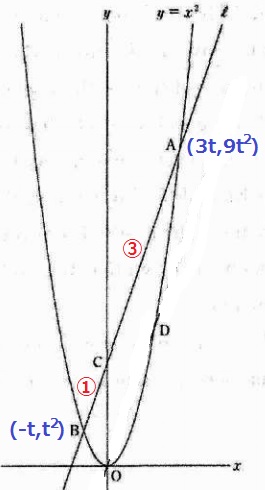
ＡＣ：ＣＢ＝３：１より、Ｂのｘ座標を－ｔとすると、
Ｂ（－ｔ、ｔ²）Ａ（３ｔ、９ｔ²）
傾きで等式を立てる。
（９ｔ²－ｔ²）÷｛（３ｔ－（－ｔ）｝＝３
２ｔ＝３
ｔ＝３/２
Ｂ（－３/２、９/４）

Ｂ⇒Ｃは右に３/２、上に３/２×３＝９/２移動するので、
切片は、９/４＋９/２＝27/４
ｙ＝３ｘ＋27/４

②

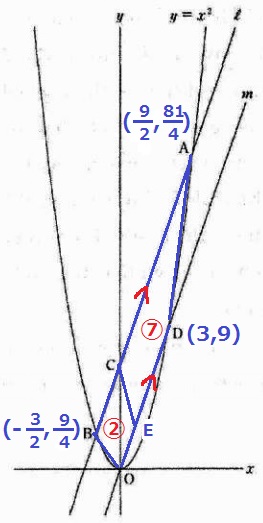
台形ＣＢＯＥ：台形ＡＣＥＤ＝②：⑦
ＡとＢ、ＤとＯのｘ座標の差はそれぞれ６と３である。

ＡＢとＤＯは傾いているので、水平にみなして考える。
上底の長さ６＋下底の長さ３＝９が、面積比の②＋⑦＝⑨に等しいから、
それぞれの台形の上底と下底の長さの和は２：７になる。
ＢＡ＋ＯＤ＝９→ＢＣ＋ＯＥ＝２（ＣＡ＋ＥＤ＝７）になればいい。
ＯＥ＝２－３/２＝１/２
ＥＤ＝３－１/２＝５/２
ＯＥ：ＥＤ＝１/２：５/２＝①：⑤

Ｅのｘ座標は、３×①/⑥＝１/２
ＯＤ；ｙ＝３ｘだから、ｙ座標は３/２。
（１/２、３/２）

大問２（英語）

５月21日金曜日19時50分、アリーシャより。

こんにちは、皆さん。あなたたちに素晴らしいお知らせを伝えたいです。
まずはこのメールを読んでください。

　やぁ、アリーシャ。元気かな？ウィスコンシン州の生徒たちが来月、私たちの町にやってくるのを知ってる？彼らはホームステイのあいだ、青空中学校に通う予定なんだ。私たちは彼らと一緒に放課後の活動をしたり、土曜日のイベントに参加する高校生を探しているの。英語や国際交流に関心がある友達を連れてきてよ。予定表を送るね。君の友達にこれを見せて、どれくらい参加するか私に教えてね。メール待ってます。では。

　これは、私の新しい友人である高橋さんからのメールです。先月、外国人向けの折り紙教室で彼女に会いました。彼女は日本文化の講座を教えているボランティアの１人です。高橋さんはとても元気の良い方で、笑顔が可愛らしいです。彼女が自分の家族について教えてくれました。彼らは多くの野菜や果物を栽培する（農家）です。私たちは折り紙や日本文化について楽しく話しました。彼女は何年も町の国際交流に関するプログラムのボランティアを務めています。ある日、彼女は言いました。「以前、私が教える別の日本文化の講座で、あなたの高校の生徒に会った」と。
　私は高橋さんから高校でウィスコンシンの生徒達に茶道を開くように頼まれました。生徒たち全員が日本の茶道に興味津々なので、茶道部の顧問である山田さんに彼らのために茶道を開催するように頼みました。彼は言いました。「それは素晴らしい経験になりますね。水曜日の放課後に茶道を開けますよ」私はこのことを高橋さんに伝えると、彼女はとても喜びました。彼女は言いました。「ウィスコンシンの生徒たちは予定を変えて、あなたの高校に行きますよ」。
　ウィスコンシンの生徒達の予定表を見て下さい。彼らは５日目に町の博物館とお城を訪れることになっています。英語と日本語の両方で私たちの町について話し合う絶好の機会になります。２年前に私がはじめてこの町にきたとき、ホストファミリーがその城に連れてくれたのです。お城の博物館ではじめて着物を着たときはとても興奮しました。彼らも同じ体験ができるでしょう。彼らにとっても私たちにとってもワクワクするイベントになります。
　もし、ウィスコンシンの生徒達と一緒に行う活動やイベントへの参加に興味がありましたら、私にメッセージを送るか、私のクラスにきてください。１年Ａ組にいます。

＠青空タウンでの滞在予定表＠
１日目：成田国際空港
　―青空中学校でオリエンテーション―ホストファミリーに会う
２日目：青空中学校で授業、給食―部活動
３日目：青空中学校で授業、給食―青空タウンの散策（高校生と一緒！）
４日目：青空中学校で授業、給食―部活動―町長とディナー
５日目：ホストファミリーと午前中を過ごす
　―午後２時、町の博物館―午後３時、青空城（高校生と一緒！）
６日目：ホストファミリーと１日中過ごす
７日目：送別会―成田国際空港

（１）エ→ア→イ→ウ
エ：アリーシャははじめて着物を着た。（２年前）
ア：アリーシャは高橋さんと友達になった。（先月）
イ：アリーシャは高橋さんからメールを受け取った。
ウ：アリーシャは山田さんに茶道を開くように頼んだ。
*『ask (人) to～』＝(人)に～を頼む。

（２）farmers
*高橋さんの家族は何をしているのか。
「who grow many vegetables and fruits.」にかかる先行詞を答える。
be動詞がareなので複数形。

（３）①ウ
空色高校の生徒には高橋さんを知っている人がいる。なぜなら、以前（　　　）からだ。
ア：彼らは彼女のために文化講座を催した
イ：彼らは彼女と折り紙教室を楽しんだ
ウ：彼らは彼女の日本文化の授業を受けた
エ：彼らはお城の博物館で彼女に会った
*メール文の次の段落の最後。『take a class』＝授業を受ける、授業をとる

②ア
『茶道に参加するに、ウィスコンシン州の生徒は（　　）日目の予定を変える』
*顧問の山田さんいわく、水曜に茶道を開くことができるとあるので水曜が何日目なのか。
曜日の情報が登場するのは高橋さんのメール「土曜のイベントに参加する高校生を探している」。
このイベントは最終段落の博物館とお城の見学だと思うが、つながっているか確信が持てない…。
予定表で〔With the high school students!〕があるのは３日目と５日目。
もし、３日目を土曜とすると、水曜は帰国予定日の７日目になってしまう。
ということは、５日目が土曜で水曜は２日目になる。

（４）例；Can I bring snacks？ I’d like to eat them with the Wisconsin students.（13語）
『やぁ、アリーシャ！連絡ありがとう！博物館とお城のイベントに参加したいけど、いくつか質問があるんだ。（　　　　）。明日、君のクラスに行くので、そのときに話そうよ』
*自由英作文。博物館とお城のイベントに関するアリーシャへの質問文を書く。
内容は何でもいい。サボの手元にある解答では日時場所を尋ねていた。
When and where will we meet? Do I need anything?『いつどこで会う？何か必要？』
サボの解答はお菓子にしました。

大問３（英語）

①私はこの記事をネットで読んだ。
コッツウォルズの石は、イギリスのコッツウォルズ地方でしか見られない天然の石です。はちみつの色をしているので、”はちみつの石”と呼ばれています。〔そこの古い家の壁は、その石でできています〕。はちみつ色の家の景色と人々の笑顔は、まるで絵本の世界にいるような気持ちにさせてくれます。コッツウォルズの村はその魅力によってイギリスで最も美しくなりました。毎年、世界中から大勢の人々が訪れます。村を歩き回ってみると安らぎを感じるだけでなく、人々がこの地方を愛する理由を知るでしょう。

②この記事でコッツウォルズに大変興味を抱き、私はコッツウォルズにあるカッスルクームの村役場にメールを送った。幸い、村に住む１人の女性と知り合いになった。彼女は、カッスルクームは『イギリスで一番可愛らしい村』と呼ばれていると私に教えてくれた。コッツウォルズの人々や多くのボランティアは長い間、その景色を守ることに努めてきた。また彼女は、約１世紀のあいだ、世界中の観光客がこの絵本の世界を体験して、その魅力を楽しんできたことも私に教えてくれた。

＜わかったこと、考えたこと＞
コッツウォルズに住む人々は、何年間も美しい景観を保つために家を管理してきた。彼らはコッツウォルズの美しさと歴史に誇りをもっている。観光客は美しい景色と心温かい人々に魅了されている。

＠＠
ここまで書いたら写真の１枚くらい載せてほしいよ (*´·ω·)(·ω·`*)ﾈｰ

VELTRAより、妖精が飛んでそうですね。

（１）イ
*「those stones」があるので、手前に石の説明が書かれている場所を選ぶ。
『be made of～』＝～からできている。
加工して見た目が変わると、『be made from～』を使う。
e.g.) Wine is made from grapes.
e.g.)Grapes is made into wine.

（２）taking care of
*これは難易度高かった(´ﾟдﾟ｀)
「People in Cotswolds ～ have worked to protect the scenery for a long time」
コッツウォルズの住民は長い間、その景色を守ってきた。
具体的にどう守ってきたのか。それをうかがい知れるのは前問の文章、
すなわち、家の壁がコッツウォルズでしか見られない石でできていること。
１軒のお宅だけ普通の壁にしてしまうと、村の趣きが台無しになってしまう。
美観風致を維持するには、村人全員が協力しなければならない。
”景色を守るために、自分たちの家（their houses）をどうするのか”⇒注意深く(carefully)扱う。
これを意味する３語のイディオムは『take care of～』になる。

「世話」の訳に引っ張られると、なかなか出てこない！
『care』は気を使う、気にかける。『take』は責任などを引き受ける。
『take care of～』で、～に気を使うことに責任を持つ。
ここから「世話をする、大事にする、面倒をみる」といった訳があてられる。
解答は現在完了進行形をとる。

大問４（国語）

〔問題文は湯川秀樹『知魚楽』〕
（１）Ⅰ：僕に君のことはわからない。（13字）
Ⅱ：君は魚ではない。（８字）
Ⅲ：君に魚の楽しみはわからない。（14字）
*論理問題で頭がごちゃりやすいが、流れをシンプルに整理する。

①荘子「あれが魚の楽しみだ」
②恵子「荘子≠魚だから、荘子に魚の楽しみはわからない」
③荘子「恵子≠荘子だから、恵子に荘子のことはわからない」
—問題文—
④恵子「恵子≠荘子だから、（　Ⅰ　）」
⑤恵子「（　Ⅱ　）だから、（　Ⅲ　）」

最後のⅢは荘子の「あれが魚の楽しみ」に対する反論なので、『君に魚の楽しみはわからない』。
恵子の論法は「〇〇ではないので、〇〇はわからない」という形なので、
Ⅲの前提であるⅡは「君（荘子）≠魚」、すなわち、「君は魚ではない」になる。
Ⅰの内容は③と④で被っているので、「僕（恵子）に君（荘子）のことはわからない」。

（２）①イ、②ア、③ア
*論法が理路整然なのは恵子の方である。荘子の「君は僕じゃない」という反論を巧みに使って、
「君は魚じゃない。だから君は魚のことがわからない」と単純明快な道筋で合点がいきやすい。
（いちいちそんなことに突っかかって自慢げなのは面倒くさいが）
一方で、荘子の最後の反論は意味わからん(´・_・`)
「僕がそう思ったからわかったのだ」と言い張っている感じで、
恵子に論理的な反論ができず、苦し紛れに虚勢を張ったように思える・・。

さらに、うしろの文も手がかりになる。
『また魚の楽しみというような、はっきり定義もできず、実証も不可能なものを認めないという方』
→魚の楽しみなんてわかるはずがない！のは恵子のスタンス。
①＝恵子、②＝荘子

恵子の論法の論理性を評価したうえで、『しかし』と逆接につながるから、
科学者であるにも関わらず、筆者は荘子の考えに強く同意したいという流れになる。
③＝荘子

（３）サボの解答例は後ほど書きます。
*サンプル問題も難しかったが、本番もやばかった(;´Д｀)
試験時間は延長した方が良いと思う。解答用紙は９行あるが、うまくまとめないと漏れる…。

荘子と恵子の問答は、科学の合理性や実証性に関わりをもっているという。
『科学者のものの考え方は、次の両極端の間のどこかにある』
『一方の極端（恵子風の考え）は、「実証されていない物事は一切、信じない」という考え方』
『他の極端（荘子風の考え）は、「存在しないことが実証されていないもの、起こり得ないことが証明されていないことは、どれも排除しない」という考え方である』

科学の伝統的な立場は、はっきりと定義ができず、実証が不可能なものを認めなかった。実証によって確実に正しいといえる事物を積み重ね、新たな真実を発見していくスタイルである。
しかし、原子の存在がわからなかった当時、原子抜きで自然現象を理解しようとした科学者より、実証されていない原子から出発した科学者のほうが深くかつ広い自然認識に達していた。
素粒子の段落の最後『今までの常識の枠を破った奇妙な考え方をしなければならないかもしれない。そういう可能性を、あらかじめ排除するわけには、いかないのである』
未だ実証はされていない可能性が一応正しいものと仮定して思考することも大事である。（荘子派）

一方で、『実証的あるいは論理的に完全に否定し得ない事物は、どれも排除しないという立場が、あまりにも寛容すぎることも明らかである。科学者は思考や実験の過程において、きびしい選択をしなければならない。いいかえれば、意識的・無意識的に、あらゆる可能性の中の大多数を排除するか、あるいは少なくとも一時、忘れなければならない』
とりうる可能性の中で本当に必要な可能性だけを選びとらなければならない。
そのためには、大多数の不要な可能性を頭の中から排除することが求められる。（恵子派）

問われているのは、『科学者の研究に対する姿勢についての筆者の考え』。
まずは、恵子的な考えと荘子的な考えをおさえること。対比構造が書きやすい。
『実際、科学者のだれひとりとして、どちらかの極端の考え方を固守しているわけではない。
問題はむしろ、両極端のどちらに近い態度をとるかにある』

概念図を描くとこんな感じでしょうか。
全体集合Ｕを「あらゆる可能性」として、真ん中にある小さいのが実証された事物とすると、
可能性を排除し過ぎて面積が小さい科学者Ａは恵子派。
可能性の排除が緩くて面積が大きい科学者Ｃは荘子派。
『科学者のものの考え方は両極端の間のどこかにある』

…しかし、これだけだと事実の摘示で終わってしまう(´д`)…
２つの考え方があって科学者は一方の極端にあるのではなく、どちらかに針が振れている。おわり
筆者の考えを直接的に記す明文が見当たらず、答案の構成を練るのがとてもシビアである。

ここで、私の手元にある解答（公式解答？）を著作権法32条の要件を充足する形で引用します。

■（手元にある）解答例■
恵子は「実証されていない物事は一切、信じない」という科学の伝統的立場に、荘子は「存在しないことが実証されていないものは、どれも排除しない」という考え方にそれぞれ近く、二つは両極端にある。科学では、思考や実験の過程で可能性の大多数の排除が必要である一方で、常識の枠を破った考え方が科学の発展へつながることもある。科学者は両者のどちらに近くても、あらゆる可能性をどこまで排除するかを考える姿勢が大切だ。

　両極端の考え方を指摘したうえで、キーとなる文もきちんと含んでいます。２つの考え方に優劣はなく、筆者は荘子派のようですが、「恵子派ではなく荘子派になるべきだ！」」とは書かれていません。最後の締めで相対する考え方をどう調和して書けば良いのか、悩んだ生徒は多かったと思います。先の解答例では、２ヶ所の段落の最後で『可能性』『排除』が重ねて登場することに着目して、科学者のあるべき研究姿勢をうまい具合にまとめています。さすが国語のプロ…。
実はサボも最初は似た流れを思いついたのですが、素粒子の段落でひっかかる点がありました。

　素粒子は原子よりもさらにミクロで、物質を構成する最小単位（現代物理学の世界では素粒子を研究する量子力学が今、熱いらしい）。素粒子は小さすぎてそれ自体を目で捉えることはできない。素粒子をよく見るには、別の素粒子を加速器であてて反応の様子を調べるほかない。しかも、反応の現場は見えず、衝突前後の反応の変化しか実験ではつかめられない。このようなもとでは、物理学者は『両極端のどちらかに偏りやすい』。ある人は恵子のように振舞い、私（筆者）は荘子のように振舞う。素粒子の心を知るには、『今までの常識の枠を破った奇妙な考え方をしなければならないかもしれない。そういう可能性を、あらかじめ排除するわけには、いかないのである』

　最後の一文には、科学者としての筆者の主観が強くにじみ出ているように思えます。文章全体を俯瞰すると、筆者は科学者の考え方について客観的な立場から解説しており、理路整然に淡々と叙述しています。個人的な意見を個人的な意見としてあまり表に出さない性格なのでしょうか。ですが、この一文は語気が強く、思い切って自分の矜持を貫いた感じがします。湯川秀樹が授与されたノーベル賞の受賞理由である中間子論の予言が実を結んだのは、常人では考えられない可能性を排除しなかったのが大きかったのかもしれません。『私自身は科学者の一人であるにもかかわらず、荘子の言わんとするところの方に、より強く同意したくなるのである』。自分みたいな荘子寄りの科学者だけでなく、恵子寄りの態度をとる科学者もいて、さまざまな立場から意見をかけ合い、互いを刺激して新しい理論を見出していく。しかし、恵子寄りの態度であっても、最初はとりうる可能性の枠を窮屈にしてはならない。あらゆる可能性をテーブルに並べ、そのあとで吟味に吟味を重ねて選択して排除すればいい。実証性がないからとしていきなり切り捨ててしまう姿勢では自然認識が曇ってしまい、素粒子の心は一向に知り得ない。湯川ドクターが考える科学者のあるべき研究姿勢はここにあるのではないかと。

■サボの解答例■
科学者には２つの考え方がある。１つは実証されていない物事を一切排除する考えで、もう１つは実証の可能性があれば、いかなる物事も排除しない考えだ。科学者は思考や実験の過程では、あらゆる可能性の大多数を排除しなくてはならない。一方で深遠な自然認識に達するには、常識の枠を破った奇妙な考えをする必要もある。科学者はあとで厳しい選択を行うにしても、そういう可能性をあらかじめ排除しない、広い視野をもたなくてはならない。

ご意見のある方は下のコメント欄かお問い合わせよりお知らせ願います。

＠2022年度千葉解説＠
数学…平均51.5点　社会…平均56.3点　理科…平均52.7点　英語…平均58.7点　国語…平均47.7点
公立高校入試解説ページに戻る