平均20.2点(前年比;-0.9点)
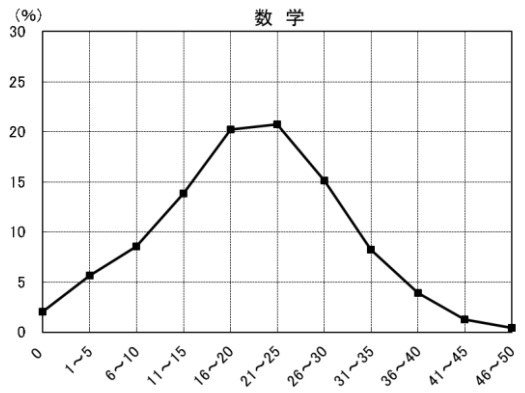
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 86.1%
3-24÷(-4)
=3+6
=9
(2) 88.7%
3(4x+y)-5(x-2y)
=12x+3y-5x+10y
=7x+13y
(3) 87.0%
√45-√5+√20
=3√5-√5+2√5
=4√5
(4) 55.1%(部分正答5.1%)
x2y-4y
=y(x2-4)
=y(x+2)(x-2)
(5) 70.2%(部分正答4.5%)
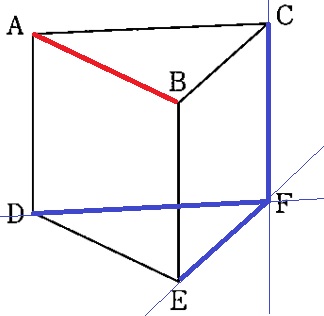
ネジレ…平行ではない、かつ延長しても交わらない。
辺CF、辺DF、辺EF
(6) 76.9%(部分正答0.4%)
反比例の比例定数aは積xyで一定。
a=-3×2=-6
(7) 66.3%(部分正答0.2%)
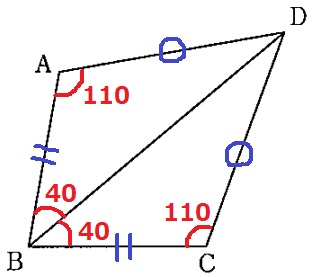
見るからに合同(3辺が等しい)
∠ADC=360-(40+110)×2=60°
(8) 72.6%(部分正答0.3%)
14/40=0.35
大問2(小問集合2)
(1) 13.0%!

ミルクティーは、紅茶:牛乳=②:①
コーヒー牛乳は、牛乳:コーヒー=△1:△1
和の③=△2が等しい量なので、最小公倍数6で比を統一する。

□5=350mLである。
紅茶…350×4/5=280mL
コーヒー…350×3/5=210mL
(2) 1.7%!!
最短距離なので展開図を描く。
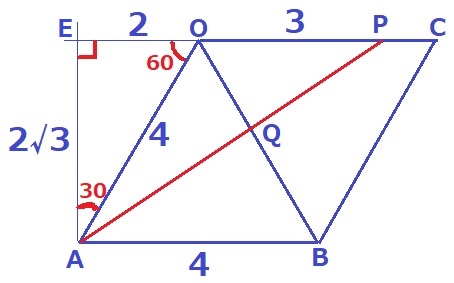
APを斜辺とする直角三角形をつくる。
COを延長、Aから垂線をひいて交点をEとする。
△AEOは1辺4cmの正三角形の半分で辺の比は1:2:√3。
EO=2cm、EA=2√3cm
△AEPで三平方→AP=√37cm
(3) 20.6%!(部分正答0.4%)

①:2019年のQ2(中央値)は1000匹未満。
30日の中央値は15番目と16番目の平均。1000匹未満は少なくとも15日以上ある。〇
②:2019年の最大値も7000匹に達していない。×
③:2021年の箱(Q1~Q3)に注目する。
Q1~Q3はデータ全体の約50%で、この箱が3000~10000をはみ出ているということは、
3000~10000は50%未満(15日未満)になる。×
(Q1は8番目の値で3000匹未満、Q3は23番目の値で10000超)
④:2019年のQ3は2000匹未満→4000匹以上は25%もない。
2021年のQ2は4000匹を超える→4000匹以上は50%を超える→2倍以上ある。〇
①、④
*ホタルが激増したのは、2020年の自粛効果が翌年に現れたからか?
大問3(関数)
(1) 34.4%(部分正答0.3%)
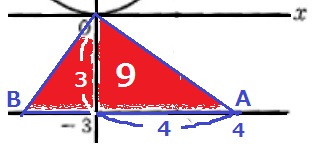
x軸より下をみる。
底辺は、9×2÷3=6
Bからy軸との距離は、6-4=2
Bのx座標は-2
(2) 10.7%!(部分正答0.1%)
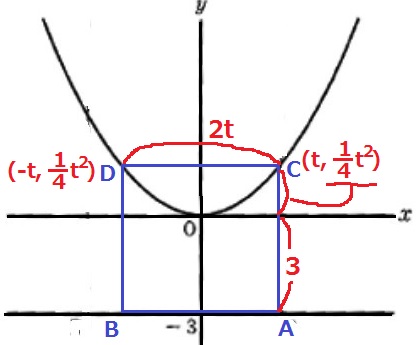
求めたいAのx座標をtとする。
Aはx>0の範囲を動く点なのでt>0
C(t、1/4t2)、D(-t、1/4t2)
正方形は横と縦の長さが同じ。
CD=2t
CA=1/4t2+3
1/4t2+3=2t
t2-8t+12
=(t-2)(t-6)=0
t>0だから、t=2、6
Aのx座標は2、6
大問4(平面図形)
14.0%!(部分正答45.8%)
△AEC∽△ABDの証明。

半円の弧に対する円周角で、∠ACE=∠ADB=90°
AC//ODの錯角で、∠CAE=∠ADO
半径より△OADは二等辺三角形。底角から∠ADO=∠DAB
2角が等しいので∽
大問5(数量変化)
(1) 48.2%(部分正答0.4%)
(0、100)⇒(4、92)
右に4、下に8だから、傾きは-8/4=-2
切片は100
y=-2x+100
(2) 11.9%!!(部分正答5.8%)
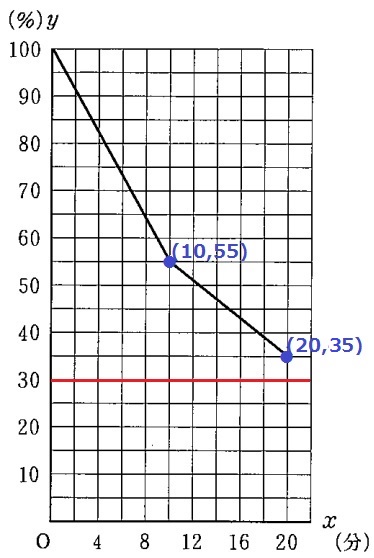
Q島までは12km。
ドローンは分速1.2kmで飛行するので、12÷1.2=10分後にQ島に到着する。
5kgの荷物を載せた場合は、(0、100)⇒(4、82)
右に4、下に18だから、傾きは-18/4=-9/2
10分後は、10×(-9/2)=45%減少する。
グラフの前半は(0、100)と(10、55)を結ぶ。
帰りも10分後に到着する。
前問より傾きは-2なので、10×(-2)=20%減少
(10、55)と(20、35)を結ぶ。
『ドローンがP島に帰る20分後のバッテリー残量が30%以下にならないため、
A社のドローンは宅配サービスに使用できる』
大問6(確率)
(1) 72.8%(部分正答0.3%)
Bに止まるには1を出すので、確率は1/4
(2) 9.4%!!(部分正答11.8%)
答案では理由も記述する。
●先手の太郎が勝つ
太郎がまず1を出してBに止まる。
次郎は残る3枚のうち4以外を出す。
1/4×2/3=1/6
●後手の次郎が勝つ
太郎は1以外を出してB以外に止まる(確率3/4)
次郎がBに着く⇒太郎と次郎の和が5になる。
2+3=3+2=4+1
↑太郎の数字と次郎の数字はかぶらない。
残りの3枚から適切な1枚を選べば、次郎はBに着く。
3/4×1/3=1/4
1/6<1/4だから、後からカードを取り出す人が勝ちやすい。
ウ
@余談@
順番を入れ替えるだけで勝率が変わるという点に関連して、
モンティ・ホール問題という数学の世界で有名な確率にまつわるトピックがあります。

高校数学の美しい物語より。
結論をいうと、扉を変えた方が当たりの確率は上がります。
詳細はリンク先を読んでください。
高校数学では”条件付き確率”で扱います。
『新情報を得ると確率は変動する(可能性がある)』ということはおさえておきましょう。
●講評●
大問1
全問正解したい。
(4)平方の差に注意。
(7)等辺に印をつけよう。
大問2
(1)中学受験に出てくる。
ミルクティーと牛乳が等量である点に注目して比を統一する。
もちろん方程式でも解ける。
(2)側面が正三角形であることをおさえる。
求めたい線分がナナメ⇒それを斜辺とする直角三角形を作成。
(3)③その範囲から箱がはみ出している⇒その範囲は50%未満。
大問3
(2)いたるところで出題される形式である。
大問4
証明も素直であった。
大問5
文字数は多いが、内容はそれほどでもない。
(1)下線部の2点が通る直線を答える。
(2)片道の距離とドローンの速さから片道の時間を出す。
荷物がない帰りの傾きを求めれば、前問の解答と合わせてグラフが完成する。
記述は20分後の残量が30%以下であるかないかに言及する。
大問6
ここも文字量に騙されてはいけない。
(1)瞬殺できる。
(2)答案では各々の確率を比較するだけで足りる。
太郎と次郎の取るべきカードを慎重に認定していく。
採点上の注意では『記号と理由がともに合っているものだけを正答』とあるが、
記述式なのでいずれかの確率が当たっていれば部分正答になるはず。



コメント