平均32.0点(前年比;+2.1点)
問題はこちら→東進ハイスクールさん(解答)
大問1(計算)
(1)
4+(-8)
=4-8
=-4
(2)
10÷(-5/4)
=-8
(3)
4+3×(-2)
=4-6
=-2
(4)
3√2+√8
=3√2+2√2
=5√2
(5)
2a×(-3a)2
=2a×9a2
=18a3
(6)
2(x+5y)-3(-x+y)
=2x+10y+3x-3y
=5x+7y
大問2(小問集合)
(1)
3:8=x:40
内項と外項の積で、8x=120
x=15
(2)
有理数→整数の分数で表せる、無理数→整数の分数で表せない。
-5=-5/1、√9=3=3/1
0は0/x(x≠0)で表せる。
√3だけ無理数。
イ
(3)
ペンは83a円、テープは102b円。これらの和が740円以下。
83a+102b≦740
ウ
(4)
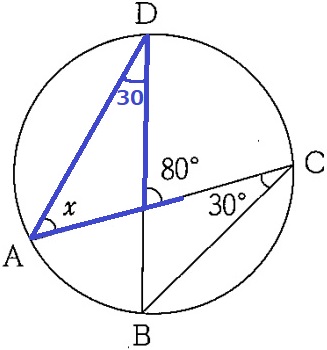
弧ABに対する円周角で、∠ADB=30°
青線の三角形で外角定理→x=80-30=50°
(5)
(2x+y)2
=4x2+4xy+y2
(6)
x2+5x-6
=(x+6)(x-1)
(7)
x2+3x+1=0
解の公式を適用して、x=(-3±√5)/2
(8)
税抜き価格を【100】とすると、税込みは【108】
6000×108/100=6480円
ウ
*マンゴーの生産量1位は沖縄。
(9)
8人の中央値(メジアン)は4番目と5番目の平均。
7と9の平均で8冊。
大問3(確率)
(1)
ゴールがスタートの原点にくるには、同じ数を異色で出す。
同じ数は1~3の3通り
色の出し方は赤⇒白、白⇒赤の2通り
3×2=6通り
(2)
2の位置にくるパターンを考える。
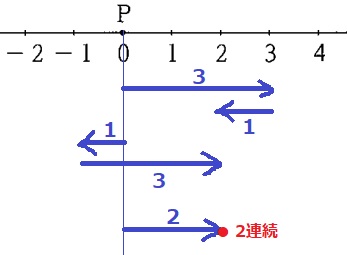
●右に3、左に1⇒(白3、赤1)
●左に1、右に3⇒(赤1、白3)
●右に2、不動⇒(白2、白2)
計3通り
全体は6×6=36通りなので、確率は3/36=1/12
(3)
-4以上のパターンが圧倒的に多い。
-5以下になるパターンを探して余事象で求める。
(赤2、赤3)(赤3、赤2)
留意すべき点は(赤3、赤3)だと-3で止まってしまうこと!
2通りしかない。
-5以下の確率は、2/36=1/18
-4以上の確率は、1-1/18=17/18
大問4(作図)
(1)
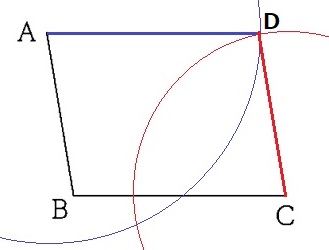
平行四辺形は2組の対辺が等しい→AD=BC、AB=DC
BCの長さをとり、Aを中心に円を描く。
ABの長さをとり、Cを中心に円を描く。
2つの交点のうち、右上がDとなる。
①…イ、②…オ
(2)
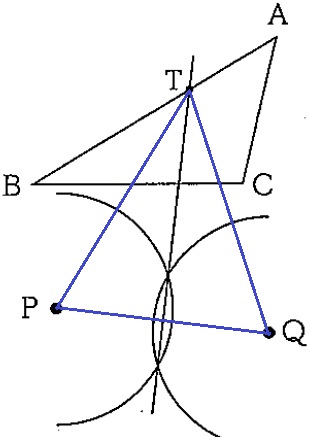
『2点P、Qから等距離にある』→PQの垂直二等分線。
△TPQの面積を最大にするので、Tは線分PQから大きく離れる。
垂直二等分線と辺ABとの交点がTとなる。
大問5(整数)
(1)
m2+n2=25(m>n)
3:4:5の直角三角形でお馴染みの三平方。
42+32=52
m=4、n=3
m2-n2=(m+n)(m-n)=4×2
m+n>m-nだから、m+n=4、m-n=2
この連立を解くと、m=3、n=1となる。
①…4、②…3、③…(m+n)(m-n)、④…3、⑤…1
(2)
前問の誘導に従う。
m2-n2
=(m+n)(m-n)=24
積が24となる組み合わせ(1を除く)は、
(m+n、m-n)=(12、2)(8、3)(6、4)
mの値を最大にするので、m+nの和が最も大きい(12、2)を選ぶ。
m+n=12、m-n=2
この連立を解いて、m=7、n=5
大問6(数量変化)
(1)
1500×30=45000円
(2)
1枚につき500円→傾きは500
初期費用50000円→x=0のとき、すなわち切片は(0、50000)
y=500x+50000
(3)
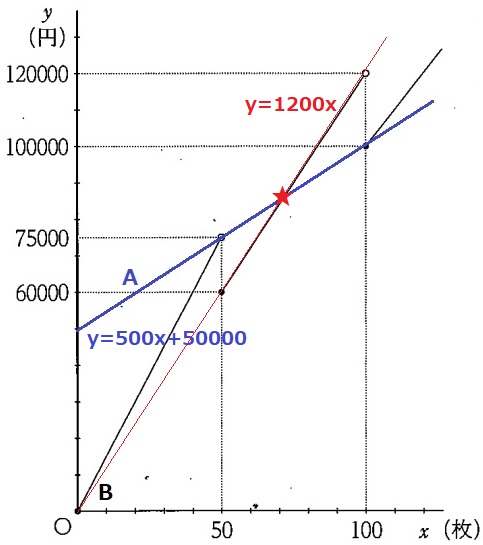
Aをグラフに追記。交点の★より下だとBの方が安い。
50≦x≦99のとき、Bの傾きは1200
50×1200=60000だから延長すると原点を通過する→y=1200x
★の座標はy=500x+50000とy=1200xの交点なので、
500x+50000=1200x
7x=500
x=71.4…
BがAより安くなるのは71枚以下のとき。
大問7(関数)
(1)
y=ax2に(x、y)=(4、16)を代入。
16=16a
a=1
(2)
y=1/2x2
x=0のとき、最小値y=0
x=4のとき、最大値y=8
0≦y≦8
(3)
y=ax2において、xの値がp→qまで増加するときの変化の割合はa(p+q)
a(-2+4)=2a
(4)
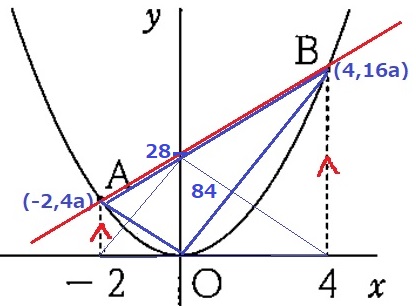
y=ax2にx座標を代入。
A(-2、4a)B(4、16a)
△OABを面積84、幅6なので、高さは84×2÷6=28
直線ABの切片は28である。
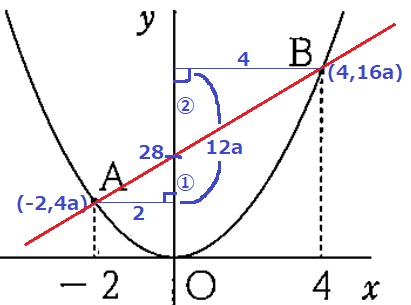
うえのような三角形の相似を描く。
相似比は2:4=①:②
y座標の差の12aが③にあたるから、①=12a×①/③=4a
切片28は、4a+4a=8a
8a=28
a=7/2
大問8(平面図形)
(1)

PQ//BRより、等角を同位角と錯角で移動させる。
△PQRは2つの底角が等しい⇒二等辺三角形
QR=PR=2cm
(2)
△APQ∽△ABRの証明。空欄補充で内容も基本レベル。

∠Aが共通角。
PQ//BRの同位角で、∠AQP=∠ARB
2角が等しいから相似となる。
A、同位角、2角
(4)
AQ:QR=3:2だから、△APQ=3cm2
△APR:△ABR=AP:AB=③:⑤
△ABRの面積は、5×⑤/③=25/3cm2
大問9(空間図形)
(1)
【球の表面積S=4πr2】
4π×32=36πcm2
(2)
【球の体積V=4/3πr3】
4/3π×33=36πcm3
*表面積と一緒!
(3)
ア:円柱Bの底面積は、3×3×π=9πcm2
(1)より球Aの表面積は36πcm2だから4倍。×
イ:円柱の側面積は6π×6=36πcm2で、球の表面積と同じ。〇
ウエ:円柱の体積は3×3×π×6=54πcm3で、球の体積はこれの2/3倍。×
イ
(4)
体積は36πcm3、底面積は9πcm2の円錐Cの高さは、
36π×3÷9π=12cm
大問10(文章題)
(1)
ルールの確認。
A:3+2=5
B:5-2=3
C:3×2=6
(2)
D:x2
C:2x2
A:2x2+2
(3)
2度やる必要がある。
A:x+2
C:2(x+2)=2x+4
D:(2x+4)2=4x2+16x+16
D:x2
C:2x2
A:2x2+2
4x2+16x+16=2x2+2
2x2+16x+14=0 ←÷2
x2+8x+7
=(x+7)(x+1)=0
x=-7、-1
(4)
2乗が数を最も大きくするので、Dを最後に持ってくる。
2乗すると符号が正になるから、方針としてはDの前までに原点0からできるだけ離す。
Dの次に数を大きくできる2倍のCが2番目。
はじめは-2と負の数から出発するので、Bで負の方向に行き、原点0から離れる。
Cでさらに負に向かい、絶対値を大きくする。
Dでさらに絶対値が多くなり、かつ符号が正に入れ替わる。
答えはB→C→D
*計算結果は144になる。
●講評●
大問数が多いので、時間との勝負になる。
大問1
全問正解ねらおう。
大問2
全部基本です。失点注意!
(2)0は自然数ではないが、整数であり有理数。
(8)算数レベル。
大問3
差が出そう。
(2)2回取らないので、数直線を使って調べてみよう。
(3)直感で-5以下が少ないとわかる。
余事象を出して、全体から引いた方が短時間でいける。
大問4
(2)『三角形の面積が最大となる』条件を見逃さない。
大問5
(2)誘導に従って1×24は除外しておく。
m>nでmを最大にするので、m+nの和を見る。
大問6
(3)60000が1200の倍数⇒グラフは原点を通過する。
大問7
(4)差が出る。
△OABの面積からABの切片が求まる。
AとBの座標を頼りに切片をaで表す。
大問8
(1)1問目なのでそんなに複雑ではない。等角の情報から入る。
ここを落とすと(3)(4)も落とす。
大問9
公式通りの計算ができれば正解できる。
(3)(4)情報を整理しよう。
大問10
ルールはわかりやすかった。
(4)方針を立てること。
数値を大きくできるものを最後に持ってくる。




コメント