2021年度　山口県公立高校入試問題過去問【数学】解説

平均25.7点（前年比；＋4.4点）
問題はコチラ→ＰＤＦファイル
出題範囲の除外はなし。大問１～３は共通問題。

大問１（計算）

（１）
－７＋９
＝２

（２）
15/２×（－４/５）
＝－６

（３）
10ａ－（６ａ＋８）
＝10ａ－６ａ－８
＝４ａ－８

（４）
27ａｂ²÷９ａｂ
＝３ｂ

（５）
３（２ｘ－ｙ）＋４（ｘ＋３ｙ）
＝６ｘ－３ｙ＋４ｘ＋12ｙ
＝10ｘ＋９ｙ

大問２（小問集合）

（１）
５で切り替わる。
小数第１位を四捨五入して40になる範囲は39.5以上40.5未満。
39.5≦ｘ＜40.5
＜

（２）
整数⇒正の整数・０・負の整数
整数どうしの和差積は必ず整数になる。
除算は割り切れなかったら整数にならない。
エ

（３）
反比例の比例定数ａは積ｘｙで一定。
ａ＝３×２＝６
ｙ＝６/ｘ

（４）
96×３÷（６×６）＝８ｃｍ

大問３（データの活用）

（１）
最頻値（モード）は最もあらわれている値。
40～50ｃｍの階級値⇒45ｃｍ

（２）
表３では階級の幅を10ｃｍに統一したが、表１・２だけで解ける。
（空欄には12＋10＝22と７＋２＝９がはいる）
おのおのの相対度数を算出し、比較すれば足りる。
Ａの相対度数…４/25＝16/100＝0.16
Ｂの相対度数…９/75＝３/25＝12/100＝0.12
0.16＞0.12ゆえ、Ａ中学校の方が60ｃｍ以上70ｃｍ未満の生徒の割合が大きい。

大問４～７は選択問題。

大問４（確率）

（１）
あたる確率が２/７。
あたらない確率は、１－２/７＝５/７

（２）
イ：試行回数を増やしていくと、ａが出る確率ａ/（ａ＋ｂ）は１/２に近づく。
大数の法則という。
ウ：確率に出てくる『同様に確からしい』とは、起こりえる結果の可能性が同じこと。
あくまで可能性なので絶対ではない。
ａの値と投げる回数が等しくなる＝すべて表がでる確率が０になるとは言い切れない。
イ・ウ

（３）
10枚から３枚を取り出す。₅Ｃ₃＝₅Ｃ₂＝10通り
和が３の倍数→位の和が３の倍数になる。
（１、２、３）
１を＋３して（４、２、３）
２を＋３して（１、５、３）（４、５、３）
以上、４通り。
確率は、４/10＝２/５

大問５（方程式）

（１）
14の平方根は±√14。
正の数だから√14。

（２）
ｘ²－２ｘ＋ａ＝０にｘ＝１＋√５を代入。
（１＋√５）²－２（１＋√５）＋ａ＝０
６＋２√５－２－２√５＋ａ＝０
ａ＝－４

＠別解＠
解の公式によると、２次方程式の解はｘ＝｛－ｂ±√（ａ²－4ａｃ）｝/２ａ
解の１つが１＋√５ということは、ルートの中のａ²－４ａｃの値が５なので、
もう１つの解は１－√５になる。（±の部分で解が２つに分かれる）

高校の数学Ⅰでは『２次方程式の解と係数の関係』という項目で、
２次方程式ａｘ²＋ｂｘ＋ｃ＝０の解をα、βとすると、
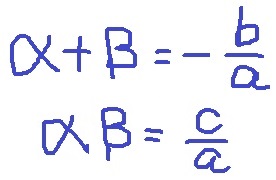になると習う。
αβ＝（１＋√５）（１－√５）＝１－５＝－４＝ｃ/ａ
本問のｘ²の係数は１だからａ＝１
ｃ＝－４

（３）
大きい方をｘとすると、小さい方はｘ－１。
ｘ（ｘ－１）＝３
ｘ²－ｘ－３＝０
解の公式を適用して、ｘ＝（１±√13）/２
小さい数は正の数⇒ｘ－１＞０
ｘ＞１だから、ｘ＝（１＋√13）/２

大問６（関数）

（１）
ｘ軸について対称移動させる。
下に凸が上に凸へ変わるから、ｙ＝－５ｘ²
－５

（２）
ア：ｙ＝ａｘ²の変化の割合は一定ではない。〇
ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）で求められる。
イ：ｘ＜０のとき、ｘが増加するとｙも増加。×
ウ：ｘ＝０のとき、ｙ＝０×
エ：ａの絶対値が小さくなるほど、グラフの開きは大きくなる。〇
ア・エ

（３）

ｙ＝－１/２ｘ²にｘ＝４を代入する。
Ａ（４、－８）
赤線の三角形が相似。
相似比は３：４だから、Ｂのｙ座標は８×３/４＝６

Ｂ（－３、６）をｙ＝ａｘ²に放り込んで、
６＝９ａ
ａ＝２/３
ｙ＝２/３ｘ²

大問７（平面図形）

（１）
半径の比は２：１。
円の面積はπｒ²だから、円の面積比は半径ｒの２乗に相当する。
円の面積比は４：１。
４

（２）

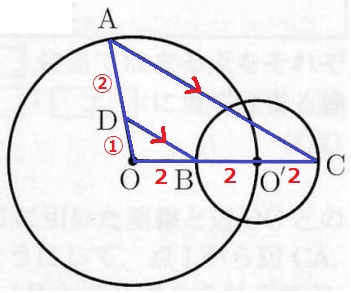
Ｏ’の半径から、ＢＯ’＝Ｏ’Ｃ＝２ｃｍ
Ｏの半径から、ＯＢ＝４－２＝２ｃｍ
△ＡＯＣ∽△ＤＯＢで、ＡＤ：ＤＯ＝②：①
ＡＤ＝４×②/③＝８/３ｃｍ

（３）

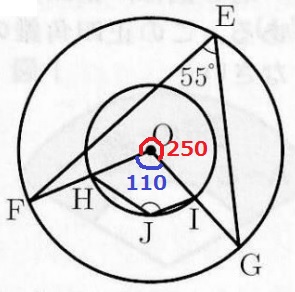
Ｅを含まない弧ＦＧに対する中心角ＦＯＧ＝55×２＝110°
Ｅを含む弧ＦＧに対する中心角ＦＯＧ＝360－110＝250°
∠ＨＪＩはこの円周角（Ｊを含まない弧ＨＩに対する円周角）なので、250÷２＝125°

＠余談＠
解答のプロセスが、円に内接する四角形の対角の和が180°である性質の証明と一緒。

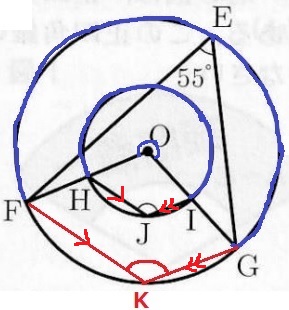
Ｅを含む弧ＦＧ（青い弧）に対する円周角が共通である。
うえのように、平行線を手がかりにＫをつくると、
内接四角形ＥＦＫＧの対角の和から、180－55＝125°

大問８～10は共通問題。

大問８（関数２）

（１）

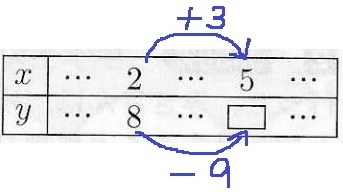
ｘの増加量は３。
変化の割合が－３なので、ｙの増加量は３×（－３）＝－９
８－９＝－１

（２）

切片の差から、ａ－ｂ＝９…②はわかりやすい。

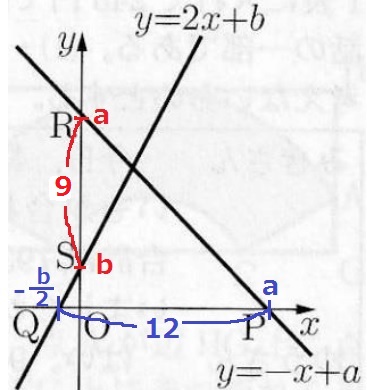
Ｐのｘ座標は、ｙ＝－ｘ＋ａにｙ＝０を代入してａ。
Ｑのｘ座標は、ｙ＝２ｘ＋ｂにｙ＝０を代入して－ｂ/２。
ａ－（－ｂ/２）＝ａ＋ｂ/２＝12　…①

①、②の連立を解くと、ａ＝11、ｂ＝２
ａ＋ｂ/２＝12、ａ＝11、ｂ＝２

大問９（平面図形２）

（１）
回転の中心を作図する。

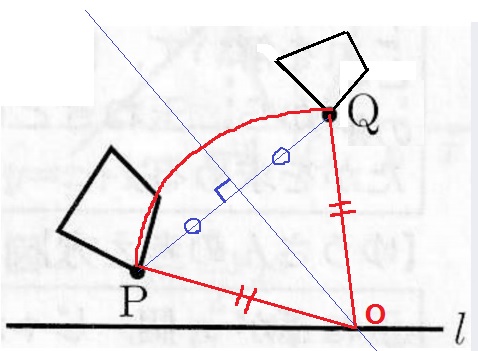
円の半径より回転の中心ＯからＰ、Ｑは等距離にある。
ＰＱの垂直二等分線は、２点Ｐ、Ｑから等距離にある点の集合。
ＰＱの垂直二等分線をひき、直線ｌとの交点がＯ。

（２）
△ＦＤＡ≡△ＦＧＢの証明。

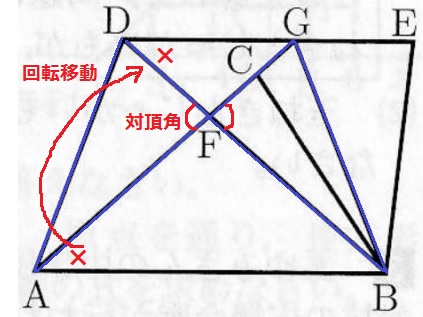
対頂角がすぐわかる。
回転移動より△ＤＢＥ≡△ＡＢＣ
求めたいのは△ＦＤＡ≡△ＦＧＢなので、
△ＤＢＥ≡△ＡＢＣの対応する辺は使いにくい。
そこで、角度に注目する。∠ＥＤＢ＝∠ＣＡＢ（×）

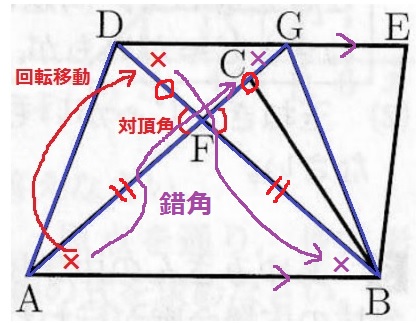
ＤＥ//ＡＢの錯角に注目すると、∠ＡＧＤと∠ＤＢＡが×で等しい。
２つの底角が等しいので、△ＡＦＢと△ＤＦＧがともに二等辺三角形。
ＦＡ＝ＦＢ、ＦＤ＝ＦＧ
２辺とあいだの角が等しいから合同といえる。

大問10（文章題）

（１）
縦に20個、横にｘ個並べて、ｘの値を１、２、３、４…と増やしたときに、
比例にならないものを選ぶ。
ア：20個、40個、60個…で比例。〇
イ：6.6ｘｃｍで比例。〇
ウ：２×（縦20個分の長さ＋横ｘ個分の長さ）＝40個分の長さ＋２ｘ個分の長さ
一次関数である。×
エ：（縦20個分の長さ）×（横ｘ個分の長さ）で比例。〇
ウ

（２）
答案では求める過程も書く。
横の長さは、6.6×105＝693ｃｍ
縦の長さは、693－300＝393ｃｍ

縦に並べる空き缶の個数をｘとする。
最初の１個は12.2ｃｍ、それ以降のｘ－１個はあいだの長さを引いた11.9ｃｍずつ増加。
12.2＋11.9（ｘ－１）＝393
11.9ｘ＝392.7
ｘ＝33
33個

（３）

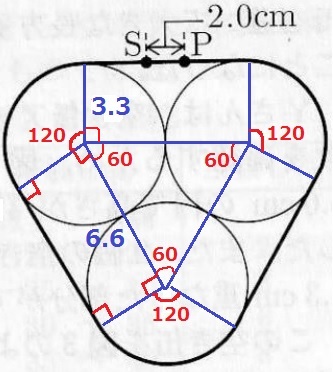
円の中心から半径を描いてみる。
曲線部分をまとめると、半径3.3ｃｍの円。
真ん中の三角形は３辺すべて6.6ｃｍの正三角形。
他の四角形は、｛360－（120＋60）｝÷２＝90°、半径と接線は垂直であるから、
すべての内角が直角なので長方形。
直線部分は6.6ｃｍが３ヶ所。これにつなぎ目の２ｃｍを足す。
6.6π＋6.6×３＋２
＝6.6π＋21.8ｃｍ
公立高校入試解説ページに戻る