2022年度　三重県公立高校入試・前期選抜過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－３²＋４×（－２）
＝－９－８
＝－17

（２）
（４ｘ＋５）－（ｘ－３）
＝４ｘ＋５－ｘ＋３
＝３ｘ＋８

（３）
ｃ＝（ａ＋ｂ）/５
５ｃ＝ａ＋ｂ
ｂ＝５ｃ－ａ

（４）
ｙ＝ｘ－３　…①
４ｘ＋５ｙ＝30　…②

①を②に代入すると、
４ｘ＋５（ｘ－３）＝30
９ｘ＝45
ｘ＝５
①に代入。ｙ＝５－３＝２
ｘ＝５、ｙ＝２

（５）
√12＋１/√３
＝２√３＋√３/３
＝７√３/３

（６）
（ｘ＋２）²＝４ｘ＋13
ｘ²＋４ｘ＋４＝４ｘ＋13
ｘ²＝９
ｘ＝±３

（７）
ｘ＝－６のとき、ｙ＝－２
ｘ＝－３のとき、ｙ＝－４
変化の割合＝ｙの増加量÷ｘの増加量
＝｛－４－（－２）｝÷｛（－３）－（－６）｝
＝－２÷３
＝－２/３

（８）
【球の体積Ｖ＝４/３πｒ³】
４/３π×３³＝36πｃｍ³

（９）

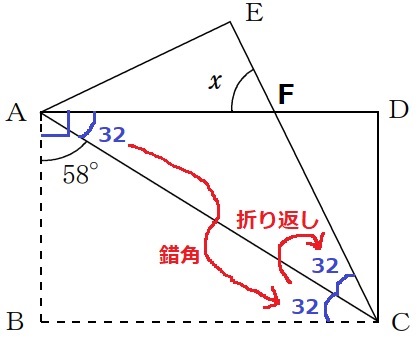
∠ＣＡＤ＝90－58＝32°
錯角で∠ＡＣＢ＝32°

ＡＤとＥＣの交点をＦとする。
折り返しで∠ＡＣＦ＝32°
最後に△ＡＣＦで外角定理→ｘ＝32＋32＝64°

（10）

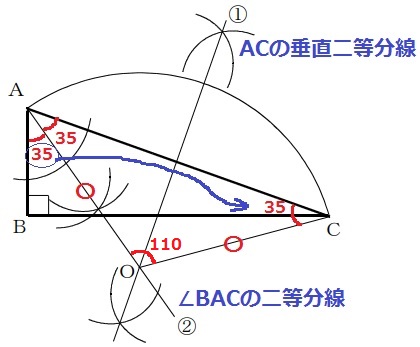
扇形ＡＯＣだから、半径ＡＯ＝ＣＯとする扇形の中心ＯはＡＣの垂直二等分線上にある。
問題は∠ＡＯＣ＝110°の作成。
具体的な数値が与えられているときは、その数値からどうやって110を作るかを考える。
180－70＝110
70°を活用したい。
△ＯＡＣが二等辺三角形である点に注目すると、その底角は（180－110）÷２＝35°
70÷２＝35だから、∠ＢＡＣを二等分すると∠ＢＡＯ＝∠ＯＣＡになり、
二等辺三角形ＯＡＣの内角が35°―35°—110°で∠ＡＯＣ＝110°となる。
⇒∠ＢＡＣの二等分線が二等辺三角形ＯＡＣの等辺ＯＡと重なる。
①ＡＣの垂直二等分線と②ＢＡＣの二等分線の交点がＯ。

大問２（データの活用&方程式）

（１）①
最頻値（モード）は最もあらわれている値。
30～35ｋｇの階級値で32.5ｋｇ。

②
27人の中央値（メジアン）は、（27＋１）÷２＝14番目
Ａ・Ｂの中央値は30～35ｋｇの階級に含まれる。
範囲（レンジ）＝最大値－最小値
範囲がＡとＢで同じということは、
Ｂの45～50ｋｇ（イ）には少なくとも１人いる。

ア＋イ＝23－（１＋４＋３＋10）＝５
Ｂの中央値（14番目）は30～35ｋｇの階級にある。
イ＝１として上から数えていくと、Ｂの30～50ｋｇの度数は、１＋０＋10＋３＝14人
イが２以上だと上から14番目が25～30ｋｇに下がってしまうので不適。
イ＝１が確定。
ア＝５－１＝４

（２）①
1000×２×80％＋200×７×80％
＝（2000＋1400）×80％
＝2720円

②
大人の入園料…1000ｘ円
子供の入園料…本来は200ｙ円だが、大人１人につき子供２人が無料なので、
大人ｘ人の場合は子供２ｘ人分が無料となる→有料の子供はｙ－２ｘ人分。
1000ｘ＋200（ｙ－２ｘ）円

③
前問の解答を利用する。
クーポンＡを使う⇒（1000ｘ＋200ｙ）×80％
クーポンＢを使う⇒1000ｘ＋200（ｙ－２ｘ）
これらの金額が等しくなるので、等式で結ぶ。

（1000ｘ＋200ｙ）×80％＝1000ｘ＋200（ｙ－２ｘ）
800ｘ＋160ｙ＝600ｘ＋200ｙ
200ｘ＝40ｙ
５ｘ＝ｙ
この等式が成り立つのは、大人（ｘ）：子供（ｙ）＝１：５

大問３（規則＆確率）

（１）①

24

②

４ｍ＋８

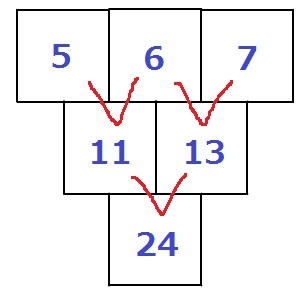
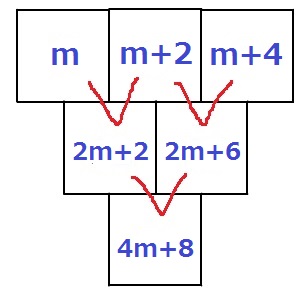
③
前問より、Ｆ＝４ｍ＋８＝４（ｍ＋２）
ということは、Ｆは４の倍数である。
４の倍数でないイ・オが正解…と思われるが、これはＡが偶数ｍの場合である。
４（ｍ＋２）＝120のときは、ｍ＝28〇
４（ｍ＋２）＝128のときは、ｍ＝30〇だが、
４（ｍ＋２）＝124のときは、ｍ＝29で前提を満たさない！！

奇数ルールの場合を調べてみると、
Ｆ＝４ｎ＋４＝４（ｎ＋１）＝124
ｎ＝30で奇数の前提を満たさず×！
124は絶対にない。
イ・ウ・オ

（２）①
ｍ＝０のとき、玉は合計で12個。
ｘ＝ｙなので袋ＡとＢで６個ずつに配分する。
玉を６個を移動させる。
和が６の組み合わせは（１、５）（５、１）（２、４）（４、２）（３、３）の５通り。
全体の出目の出し方は６×６＝36通り
確率は５/36。

②
確率が１/12＝３/36だから、和の組み合わせは３パターン。
２つの和が３パターンになるのは、４か10しかない。
また、袋ＡとＢの玉が同数になるので12＋ｍが偶数⇒ｍは偶数。
◆４個移動させる
ｘ＝12－４＝８
ｙ＝ｍ＋４＝８
ｍ＝４で偶数。〇

◆10個移動させる
ｘ＝12－10＝２
ｙ＝ｍ＋10＝２
ｍ＝－８で不適。×
よって、ｍ＝４

大問４（数量変化）

（１）

２秒後の様子。
△ＢＰＱ＝４×２÷２＝４ｃｍ²

（２）

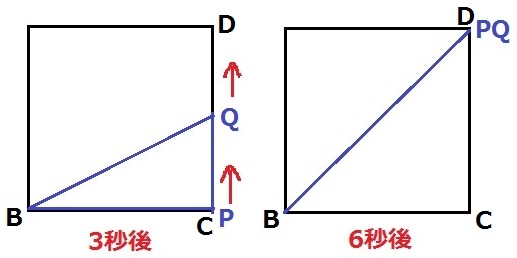
変化を確認。
３秒後にＰはＣにいて、ＱはＣＤの中点。６秒後にＰとＱは同時にＤに着く。
△ＢＰＱは底辺ＰＱが減少、高さはそのままだから一次関数で減っていき、６秒後に０ｃｍ²。

ＣＰ＝２ｘ－６
ＣＱ＝ｘ
ＰＱ＝ｘ－（２ｘ－６）＝－ｘ＋６
ｙ＝（－ｘ＋６）×６÷２＝－３ｘ＋18

（３）

０≦ｘ≦３のとき、底辺と高さが同時に増えるからｙ＝ａｘ²で増える。
ｘ＝３のとき、ｙ＝９
底辺ＰＱが縮んで一次関数で面積は減少していき、ｘ＝６のときｙ＝０
６≦ｘ≦９のとき、底辺ＰＱが伸びるので面積は一次関数で増加。
ｘ＝９のとき、ｙ＝９
イ

（４）

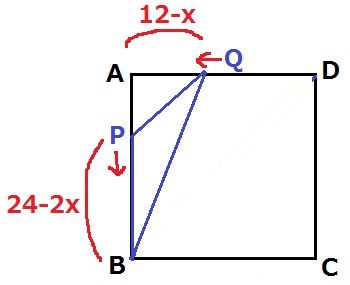
９≦ｘ≦12のとき、底辺ＰＢと高さＡＱがともに減っていく。
面積はｙ＝ａｘ²で減少し、ｘ＝12のときに０ｃｍ²となる。

ＰＢ…１周24ｃｍからＰの移動距離２ｘｃｍを引いて24－２ｘｃｍ。
ＡＱ…Ｃ～Ａの半周12ｃｍからＱの移動距離ｘｃｍを引いて12－ｘｃｍ。
（24－２ｘ）（12－ｘ）÷２
＝（288－48ｘ＋２ｘ²）×１/２
＝ｘ²－24ｘ＋144＝７

ｘ²－24ｘ＋137＝０
解の公式を適用。ｘの係数が偶数だからｂ＝２ｂ’が使える。
ｘ＝12±√（144－137）＝12±√７
９≦ｘ≦12より、ｘ＝12－√７

＠別解＠
９秒後に９ｃｍ²で、12秒後に０ｃｍ²。
３秒間で－９ｃｍ²になる。

底辺&高さ共に減少→ｙ＝ａｘ²で減少するので放物線を作成。
12秒後を原点０に設定すると、９秒後はその３秒前だから（－３、９）。
（－３、９）を通るということは、グラフの式はｙ＝ｘ²である。

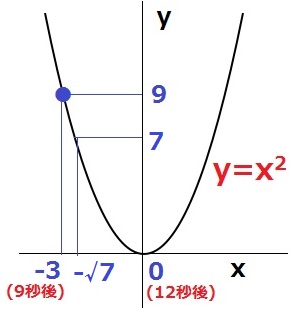
ｙ＝７のとき、ｘ＝－√７（ｘ＜０）
12秒後の√７秒前だから、答えはｘ＝12－√７となる。

大問５（平面図形）

（１）①
△ＡＢＤ≡△ＡＣＥの証明。

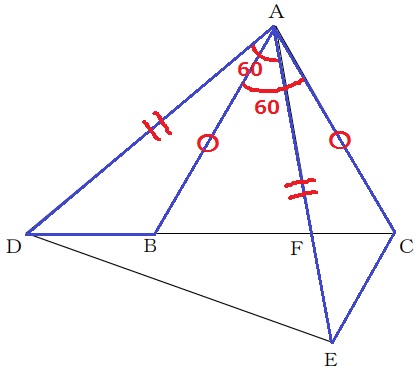
正三角形の１辺より、ＡＢ＝ＡＣ、ＡＤ＝ＡＥ
正三角形の内角は60°。あいだの角である∠ＢＡＦを引いて、
∠ＤＡＢ＝60－∠ＢＡＦ＝∠ＥＡＣ
２辺とあいだの角が等しいので合同。

＠余談＠
△ＡＢＤをＡを回転の中心として反時計回りに60度回転させると△ＡＣＥになる。

②ⅰ

△ＡＢＣは正三角形だから、ＡＢ＝ＢＣ＝６ｃｍ
外角定理より、∠ＡＢＤ＝60＋60＝120°
①の合同から対応する角で∠ＡＣＥ＝120°
∠ＢＣＥ＝120－60＝60°

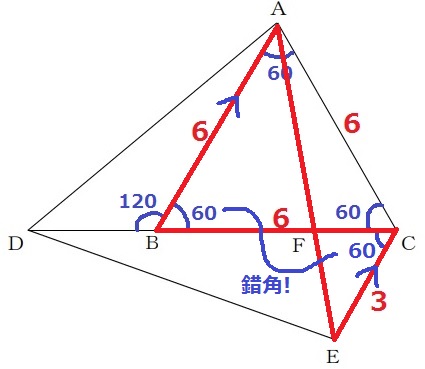
∠ＡＢＣ＝∠ＥＣＢ＝60°で錯角が等しい！→ＡＢ//ＣＥ
△ＡＢＦ∽△ＥＣＦより、ＢＦ：ＦＣ＝ＡＢ：ＥＣ＝６：３＝２：１
ＢＦ＝６×２/３＝４ｃｍ

ⅱ

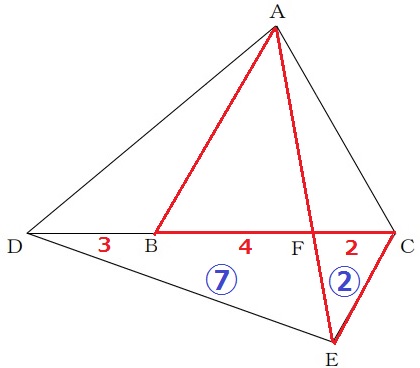
ＤＦ：ＦＣ＝７：２
△ＦＥＣの面積を②とすると、△ＤＥＦは⑦。

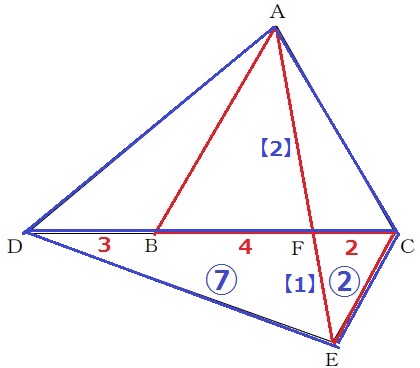
先ほどの△ＡＢＦ∽△ＥＣＦより、ＡＦ：ＦＥ＝２：１
△ＡＣＤと△ＥＣＤは底辺ＤＣが共通で高さの比が２：１⇒△ＡＣＤ：△ＥＣＤ＝２：１
四角形ＡＤＥＣの面積は、⑨（△ＥＣＤ）×【３】＝㉗
△ＦＥＣ：四角形ＡＤＥＣ＝２：27

（２）

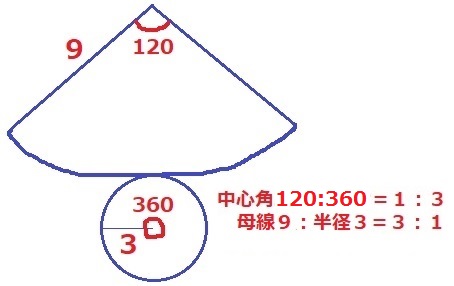
おさえておくべき点は、母線：半径の比は中心角の逆比であること！
中心角の比は扇形：円＝120：360＝１：３
母線（扇形の半径）：円の半径は逆比で３：１。
底面の円の半径は、９×１/３＝３ｃｍ
円錐の表面積は、３×３×π＋８×８×π×１/３＝36πｃｍ²
公立高校入試解説ページに戻る