問題ＰＤＦ
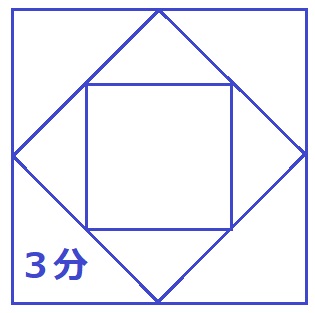
正四角柱（底面が正方形である角柱）の形をしたふたのない容器３つを図１のように組み合わせた水そうがあります。この水そうを上から見ると図２のようになり、（ア）の部分の真上から一定の割合で水を注ぎました。グラフは、水を注ぎ始めてからの時間（分）と（ア）の水面の高さ（ｃｍ）の関係を表しています。
グラフのＤが表す時間の後は、水そうの底から毎分0.8Ｌの割合で排水しました。ただし、図２で同じ印のついているところは同じ長さを表し、３つの容器の厚みは考えません。
（１）
水は毎分何Ｌの割合で注がれていたか求めなさい。
（２）
グラフのＡ、Ｂ、Ｃ、Ｄにあてはまる数を入れなさい。
＠解説＠
（１）
↑最初の３分間で埋まるところ。
20×20÷２×36÷３
＝2400ｃｍ3＝2.4Ｌ
（２）
上から見た図。
Ａは真ん中の小さい正方形を除いた部分の高さ36ｃｍ。
左下の直角二等辺が最初の３分。
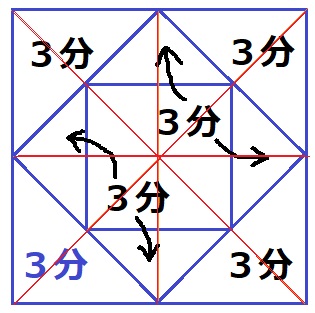
これがもう５個分あるので、全体は３×６＝18分（Ａ）
Ａから33分までは、真ん中の小さな正方形を除く部分が比例で上がっていく。
グラフの●を通過する直線をひくと原点を通過する。
36×33/18＝66ｃｍ（Ｂ）
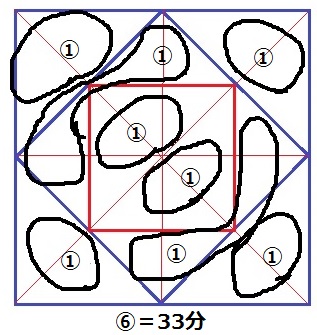
奇妙な図ですが、再び上からみた図です。
Ｃは高さ66ｃｍがすべて埋まった時間。
底面積を上のように８等分したうち、赤い正方形を除いた⑥が33分だから、
33×⑧/⑥＝44分（Ｃ）
与えられたグラフでは、うまく線が引けなかったので書き直しました。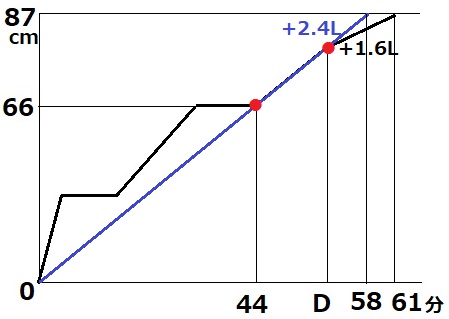
44分以降はすべての底面積が埋まっていく。
仮に排水をしなかったら、44×87/66＝58分後に満水になった。
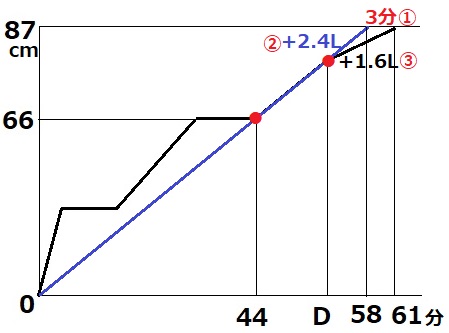
ここまでくれば見えてくるはず。
速さの比は、排水なし：排水あり＝2.4：1.6＝３：２
時間の比は逆比だから、排水なし＝②とすると、排水あり＝③
差の３分が①なので、58－３×②＝52分（Ｄ）
Ａ…18、Ｂ…66、Ｃ…44、Ｄ…52
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント