2019年度　山梨県公立高校過去問【数学】解説

平均55.6点（最高100点、最低３点）

問題はコチラ→リセマムさん

大問１（計算）

（１）　98％
６－７＝－１

（２）　85％
５/６÷（－２）＝－５/12

（３）　97％
（－10）＋（－５）²
＝－10＋25＝15

（４）　88％
９/√３＋７√３
＝３√３＋７√３＝10√３

（５）　85％
８ｘｙ²×３/４ｘ＝６ｘ²ｙ²

（６）　95％
ｘ（３ｘ－２）＋２ｘ
＝３ｘ²－２ｘ＋２ｘ＝３ｘ²

大問２（小問集合）

（１）　86％
下を上に代入すると、
２（３ｙ＋２）－５ｙ＝６
ｙ＝２
ｘ＝３×２＋２＝８
ｘ＝８、ｙ＝２

（２）　85％

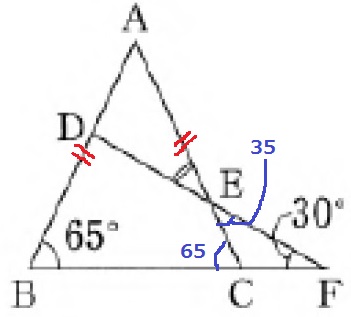
△ＡＢＣは二等辺→∠ＡＣＢ＝65°
△ＥＣＦで外角定理→∠ＣＥＦ＝65－30＝35°
対頂角で∠ＤＥＡ＝35°

（３）　77％
ア：ｙ＝－ｘ＋20（一次関数）
イ：球の表面積；Ｓ＝４πｒ²
ｙ＝４πｘ²（ｙ＝ａｘ²）
ウ：ｙ＝800/ｘ（反比例）
エ：ｙ＝３ｘ（比例）
ウ

（４）　70％（部分点２％）
５個から２個取り出す…₅Ｃ₂＝10通り
〔白が含まれている＝全体－白が含まれない〕
白が含まれない場合…赤か青の４個から２個取り出す。₄Ｃ₂＝６通り
したがって、白が出ない確率は、１－６/10＝２/５

（５）①　65％
10個のメジアン→５番目と６番目の平均。
34と35の平均だから、34.5℃

②　65％
34℃以上36°未満は５個。
相対度数は分数ではなく、小数で求める。
５÷10＝0.5

大問３（数量変化）

（１）　72％
ＢＥ＝ＢＰ＝ｘｃｍ
△ＰＢＥの面積ｙは倍々に増えていく（ｙ＝ａｘ²）。
図２のグラフから、（10、50）を通るので、
50＝10²ａ
ａ＝１/２
ｙ＝１/２x²

ｘ＝４を代入。
ｙ＝１/２×４²＝８

（２）　86％
25＝１/２ｘ²
ｘ²＝50
ｘ＞０より、ｘ＝５√２
√２＝1.41421356…（一夜一夜に人見ごろ）
５√２＝５×1.41…＝7.05…
イ

（３）①　22％！（無答38％）
△ＣＤＥ∽△ＰＢＥより、ＢＰ＝１/２ｘｃｍ
ｙ＝１/２ｘ×ｘ１/２＝１/４ｘ²
ｘの値がｔのとき、２つのｙ座標の差が９になった。
１/２ｔ²－１/４ｔ²＝９
１/４ｔ²＝９
ｔ²＝36
ｔ＞０より、ｔ＝６

②説明；31％！（部分点７％、無答53％）数量；23％！
ℓがｘの一次関数である理由を述べる。
一次関数⇒ｙ＝ａｘ＋ｂの形に変換できる。
ℓ（ＤＢ）＝10－ｘ＝－ｘ＋10
ｙ＝ａｘ＋ｂの形にできるから一次関数となる。
＠＠＠
ＤＢ以外にｘとの関係が１次関数になるのは線分ＣＰ。
△ＣＤＥで三平方をすると、ＣＥ＝５√５ｃｍ
同様に、△ＰＢＥで三平方、ＰＥ＝√５/２ｘ
ＣＰ＝－√５/２ｘ＋５√５で一次関数。

また、比例となるＰＢも正答扱いになる。（ｙ＝１/２ｘ＋０）
…ということは、ＰＥも比例なので正答（ｙ＝√５/２ｘ＋０）。
ＡＢ（封筒の縦）の長さは問題文で与えられていないが、
ＡＰ＝ＡＢ－ＰＢで、ＰＢ＝１/２ｘだから、
ＡＰ＝－１/２ｘ＋ＡＢで一次関数になる。

大問４（文字式）

（１）　91％
16＝４×４
１辺に４枚だから４ｃｍ。

（２）　29％！
２次元で書いてみよう。

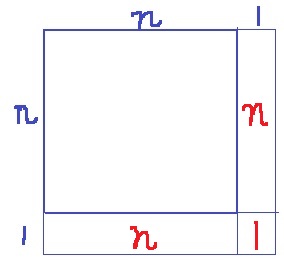
１辺ｎｃｍの正方形の外側に１ｃｍ分追加。
２ｎ＋１枚

（３）①　５％!!（部分点13％、無答38％）
証明の誤りを指摘する。
１つの囲みにあるシールの枚数は、１辺の正方形の枚数と同じｎ枚。
囲みの数は、正方形の間の数なのでｎ－１枚となる。
ｎ×２（ｎ－１）＝２ｎ（ｎ－１）枚
*囲みの数をｎ個ずつとしたままで、式のみ修正した誤答が多かったようだ。

②　23％！
２ｎ（ｎ－１）＝180
ｎ（ｎ－１）＝90
ｎ²－ｎ－90＝（ｎ－10）（ｎ＋９）＝０
ｎ＞０から、ｎ＝10
正方形の１辺は１ｃｍで10枚だから、10ｃｍ。

大問５（平面図形）

（１）　78％（部分点７％）
作図問題。レベルは基本。
①ＢＣの垂直二等分線。交点が中点Ｍ。
②ＡＭを引く。

（２）①　16％！（部分点12％、無答30％）
△ＡＤＭ＝△ＰＤＭの証明を補完する。

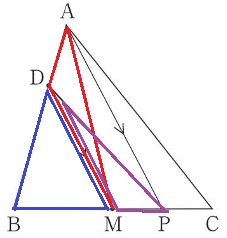
△ＡＤＭと△ＰＤＭにおいて、共通部分である△ＤＢＭに、
それぞれ△ＡＤＭと△ＰＤＭを足す。
△ＡＤＭ＝△ＰＤＭは等積変形から導くが、
なぜ、等積変形は面積が等しくなるのか。この点を補完する。
△ＡＤＭと△ＰＤＭの《底辺ＤＭは同じで、高さが等しいから》面積は等しくなる。
*部分正当例としては、「高さが等しいこと」と「底辺が共通であること」のいずれかのみの記述。
また、「平行線の錯角が等しいから」という図形の性質を根拠なく用いる誤答も多かった。

②　33％
△ＡＢＭと△ＡＢＰは高さが等しいので、底辺の比ＢＭ：ＢＰがわかればいい。

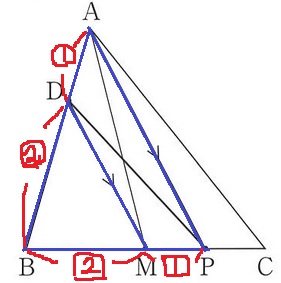
ＤＭ//ＡＰから、△ＢＤＭ∽△ＢＡＰ（平行線と線分の比）。
ＢＭ：ＢＰ＝ＢＤ：ＢＡ＝２：３
△ＡＢＭ：△ＡＢＰ＝２：３

（３）　５％!!（部分点０％、無答45％）
前問の考えを利用する。

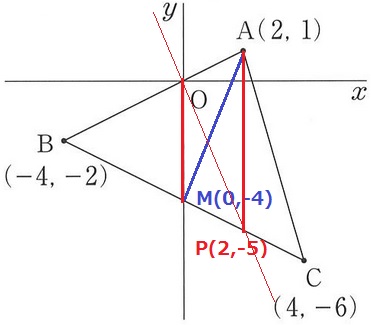
ＢＣの中点Ｍ（０、－４）とＡを結ぶ。
Ａを通る、ＯＭと平行な線をひき、ＢＣとの交点がＰ。
ＯＭがｙ軸なので、ＡＰはｘ＝２
Ｍ・Ｐ・Ｃのｘ座標（０・２・４）をみると、ＰはちょうどＭＣの中点にくる。
Ｐ（２、－５）
ＯＰの式は、右に２、下に５なので、ｙ＝－５/２ｘ

大問６（空間図形）

（１）　82％
弧ＡＢに対する円周角（∠ＡＣＢ）が45°なので、
その中心角である∠ＡＯＢ＝45×２＝90°

（２）　62％
△ＡＢＨは三角定規でおなじみの、30°－60°－90°の直角三角形。
１：２：√３より、ＡＨ＝２×√３/２＝√３ｃｍ

（３）①　32％！（部分点49％、無答10％）
△ＡＥＢ≡△ＤＥＣの証明。

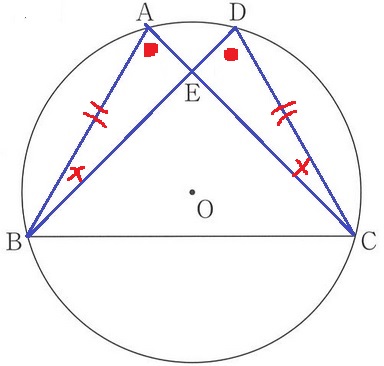
仮定より、ＡＢ＝ＤＣ
この両端角が円周角定理から等しい点を指摘する。

②　６％!!（部分点１％、無答52％）
四角形ＡＢＣＤは左右対称の等脚台形（跳び箱の形）。
（２）で高さは√３ｃｍと出したので、上底ＡＤと下底ＢＣを求める。

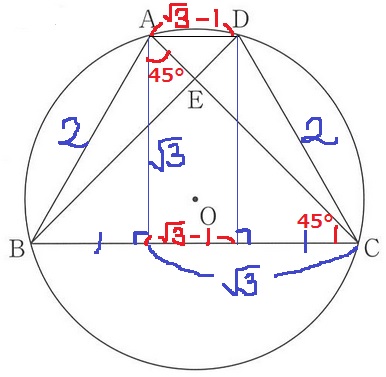
45°－45°－90°の直角二等辺から、高さ√３を下底へ移動。
下底は１＋√３ｃｍ。
真ん中の長方形の横の長さは√３－１ｃｍとなり、これが上底ＡＤの長さと等しい。
（√３－１＋１＋√３）×√３÷２＝３ｃｍ²

③　０％!!!（部分点０％、無答57％）

切り口の半径はＰＱ。
ＰＯ、すなわち、四角錘の高さが判明すれば、△ＯＰＱの三平方からＰＱが出せる。

球の半径がわかっているので、球の体積が求められる。
問題文の体積比から四角錘の体積がでる。
四角錘の底面ＡＢＣＤの面積は、前問で出した３ｃｍ²。
ここから四角錘の高さＰＯが求められる。

球の体積：４/３πｒ³
４/３π×（√２）³＝８√２/３πｃｍ³
四角錘の体積…８√２/３π×１/４π＝２√２/３ｃｍ³
四角錘の高さ…３×ＰＯ×１/３＝２√２/３
ＰＯ＝２√２/３ｃｍ

最後に、△ＯＰＱで三平方。
ＰＱ²＝（√２）²－（２√２/３）²＝10/９
ＰＱ＞０から、ＰＱ（円Ｐの半径）＝√10/３ｃｍ
公立高校入試解説ページに戻る