2022年度　京都府公立高校入試・中期過去問【数学】解説

問題はコチラ→ＰＤＦファイル
2022年度・京都（前期）数学の解説はコチラ。

大問１（小問集合）

（１）
－３²－６×５
＝－９－30
＝－39

（２）
（８ａ＋９）/４－（６ａ＋４）/３
＝｛３（８ａ＋９）－４（６ａ＋４）｝/12
＝（24ａ＋27－24ａ－16）/12
＝11/12

（３）
（√２＋√５）²
＝７＋２√10

（４）
0.16ｘ－0.08＝0.4　←×100
16ｘ－８＝40　←÷８
２ｘ－１＝５
ｘ＝３

（５）
７ｘ－３ｙ＝11　…①
３ｘ－２ｙ＝－１　…②
①×２－②×３がやりやすいかな？
ｘ＝５、ｙ＝８

（６）
ｙ＝１/４ｘ²は下に凸のグラフ。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝３のとき、ｙ＝１/４×３²＝９/４で最大値９にならない。
→ｘ＝ａのとき、最大値ｙ＝９
最大値をつくるには原点から大きく離す。
ａは原点から３より離れる負の数⇒ａ＜－３
９＝１/４ａ²
ａ²＝36
ａ＜－３より、ａ＝－６
ａ＝－６、ｂ＝０

（７）

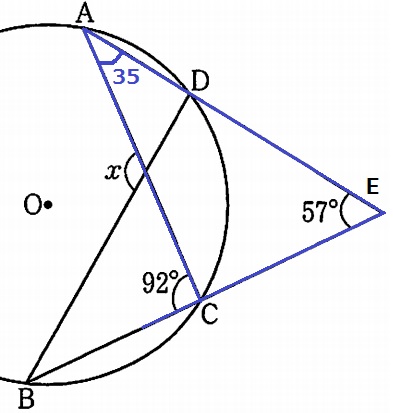
△ＡＣＥで外角定理→∠ＣＡＥ＝92－57＝35°

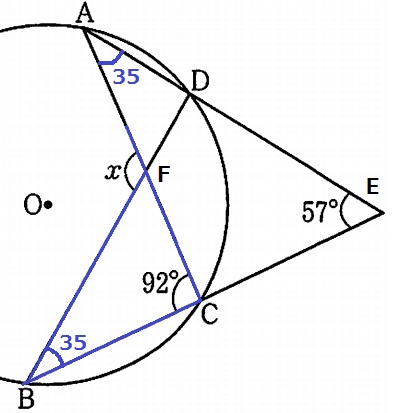
弧ＣＤに対する円周角より、∠ＣＢＤ＝35°
△ＢＣＦで外角定理→ｘ＝35＋92＝127°

（８）
無作為に抽出した40個において、黒：白＝３：37
黒は全部で50個だから、白の総数は50×37/３＝616.6…≒620個

大問２（確率）

（１）
全体は、６×６＝36通り
ａ/ｂ＝２となるのは、（ａ、ｂ）＝（６、３）（４、２）（２、１）の３通り。
確率は３/36＝１/12

（２）
循環小数とは数字の並びに周期性のある無限小数。
ｂから考える。
ｂ＝１のとき、ａ/ｂはすべて整数になるので無い。
ｂ＝２は整数か小数第１位までの有限小数。
ｂ＝３のとき、÷３すると0.333…か0.666…となる１/３、２/３、４/３、５/３。
ｂ＝４は整数か小数第２位までの有限小数。
ｂ＝５は整数か小数第１位までの有限小数。
ｂ＝６のとき、１/６＝1.666…で循環小数。
これ倍にした２/６、４/６、５/６も同様に循環小数。
計８通り。確率は８/36＝２/９

大問３（空間図形）

（１）

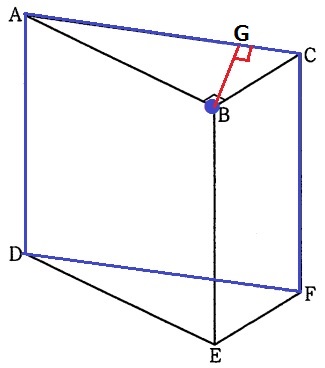
点Ｂ⊥面ＡＤＦＣの距離は、ＢからＡＣにひいた垂線の長さ。
オ

（２）

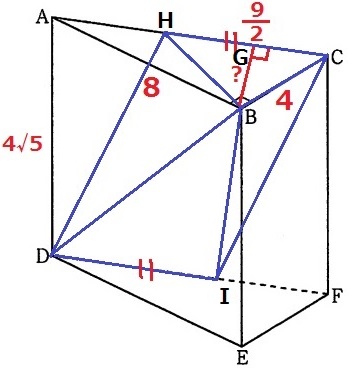
四角形ＨＤＩＣは１組の対辺が等しく、かつ平行だから平行四辺形。
これを底面としたとき、（１）のＢＧが四角錘Ｂ―ＨＤＩＣの高さにあたる。
△ＡＢＣで三平方→ＡＣ＝ＡＤ＝４√５ｃｍ

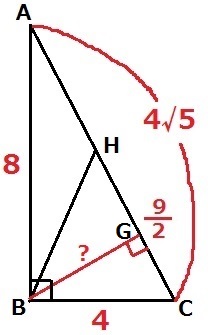
△ＡＢＣの面積を２通りで表すと、
４×８÷２＝４√５×ＢＧ÷２
ＢＧ＝４×８÷４√５＝８/√５ｃｍ
四角錘Ｂ―ＨＤＩＣの体積は、９/２×４√５×８/√５÷３＝48ｃｍ³

大問４（数量変化）

（１）

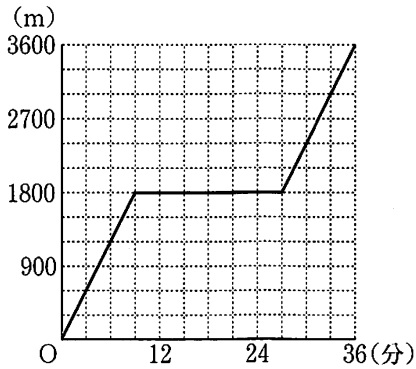
大輝が１周を走る時間は、（36－18）÷２＝９分
1800ｍを９分で走る⇒18分間休憩⇒９分間走る

（２）

グラフを追記。大輝が休憩後、ひなたに追いつく●の時間が答え。

赤線の相似比は４：１。
⑤＝９分だから、①＝９×①/⑤＝９/５分＝１分48秒
大輝の休憩が終わる９時27分の１分48秒後⇒午前９時28分48秒

（３）
なんかイヤなんですけど(´ﾟдﾟ｀)

京平は２人と反対の向きで走る。
グラフの上半分（1800～3600ｍ）に京平を追記すると、
大輝とひなたとの交点のｙ座標の差が答えになる。

３人の速さを出しておく。
京平；1800÷12＝分速150ｍ
大輝；1800÷９＝分速200ｍ
ひなた；1800÷24＝分速75ｍ

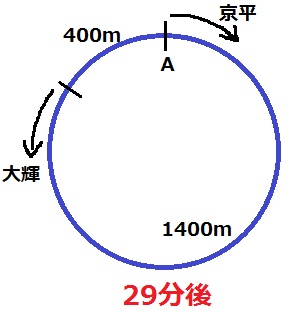
京平が出発する29分後の京平と大輝の状態。
大輝は27分にＡ地点を出発しているので、200×２＝400ｍ進んでいる。
残りの1400ｍを両者は１分あたり150＋200＝350ｍずつ距離を縮めるから、
1400÷350＝４分後に出会う。

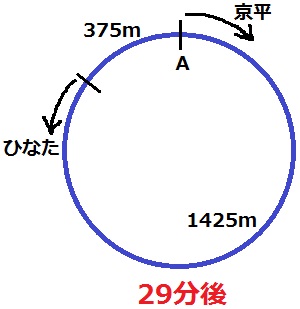
29分後の京平とひなたの状態。
ひなたは24分にＡ地点を出発しているので、75×５＝375ｍ進んでいる。
残りは1425ｍで１分あたり150＋75＝225ｍ縮むから、
1425÷225＝19/３分後

京平が大輝とすれ違ってから、ひなたに会うまでの時間は19/３－４＝７/３分
その間の移動距離は、150×７/３＝350ｍ

大問５（平面図形）

（１）

△ＡＥＦ∽△ＡＢＣより、ＥＦ＝７×６/９＝14/３ｃｍ

（２）
ここで等角の情報を使う。

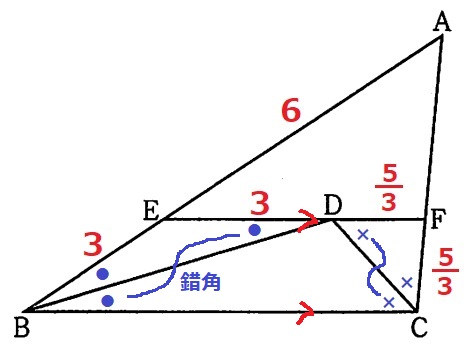
ＥＦ//ＢＣの錯角より、△ＥＢＤと△ＦＤＣは底角が等しいから二等辺三角形。
ＥＤ＝ＥＢ＝３ｃｍ
（１）よりＥＦ＝14/３ｃｍなので、ＦＤ＝ＦＣ＝14/３－３＝５/３ｃｍ
ＡＥ：ＥＢ＝ＡＦ：ＦＣ＝２：１
ＡＦ＝５/３×２＝10/３ｃｍ

（３）

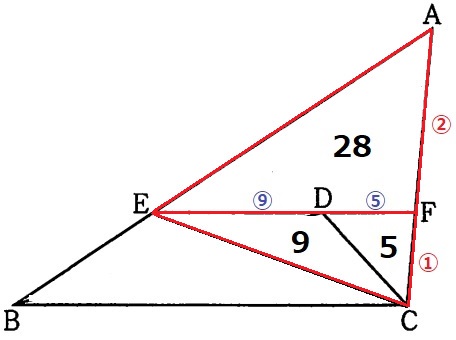
わかりやすいように△ＤＢＣを等積変形で左に寄せ、△ＥＢＣにしておく。
ＥＤ：ＤＦ＝３：５/３＝⑨：⑤
△ＣＦＤの面積を５とすると、△ＣＤＥは９。
ＡＣ：ＦＣ＝③：①より、△ＡＥＣ＝△ＦＥＣ（14）×３＝42

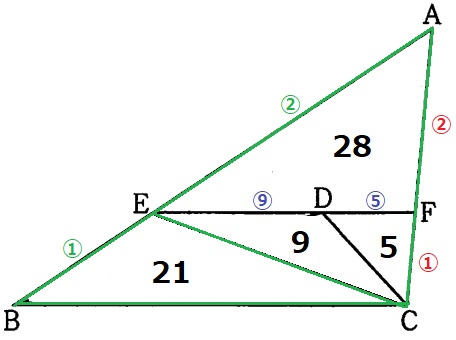
ＡＥ：ＡＢ＝②：③より、△ＡＢＣ＝△ＡＥＣ（42）×３/２＝63
△ＣＦＤ：△ＡＢＣ＝５：63

大問６（規則）

（１）

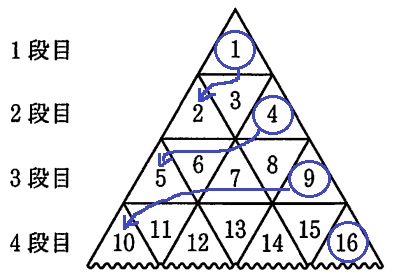
平方数が特徴なので、これに着目する。
右端は〇番目の平方数。
７番目の右端は、７²＝49

左端は〇番目の１個手前の平方数に＋１した数。
７番目の左端は、６²＋１＝37
左端…37、右端…49

（２）
ｎ段目の右端はｎ²、左端は（ｎ－１）²＋１。
ｎ²＋｛（ｎ－１）²＋１｝＝1986
２ｎ²－２ｎ－1984＝０
ｎ²－ｎ－992＝０
*30×30＝900。１の位の２は１×２⇒31×32ではないかと予想する。
（ｎ＋31）（ｎ－32）＝０
ｎ＞０より、ｎ＝32