平均点45.4点（前年比；－8.3点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）―69.9％
（１） 92.6％
２－11＋５
＝－４
（２） 88.3％
３（ａ－３ｂ）－４（－ａ＋２ｂ）
＝３ａ－９ｂ＋４ａ－８ｂ
＝７ａ－17ｂ
（３） 85.7％
８ａ2ｂ3÷（－２ａｂ）2
８ａ2ｂ3÷４ａ2ｂ2
＝２ｂ
（４） 82.9％
√６×２√３－５√２
＝２√18－５√２
＝６√２－５√２
＝√２
（５） 74.1％
ｘ2－５ｘ－６
＝（ｘ－６）（ｘ＋１）＝０
ｘ＝６、－１
（６） 58.3％
（－１、１）⇒（２、７）
右に３、上に６だから、傾きは６/３＝２
切片は（－１、１）から右に１、上に２移動して３。
ｙ＝２ｘ＋３
（７） 56.7％
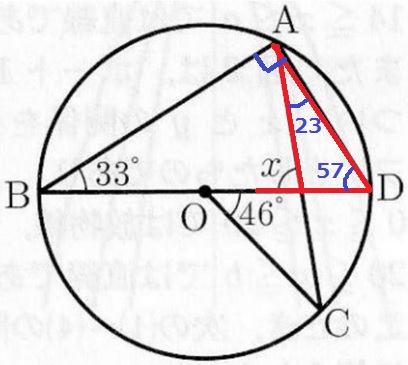
直径ＢＤに対する円周角、∠ＢＡＤ＝90°
△ＡＢＤの内角で、∠ＡＤＢ＝180－（90＋33）＝57°
弧ＣＤに対する円周角、∠ＣＡＤ＝46÷２＝23°
赤線で外角定理を使う。ｘ＝23＋57＝80°
*誤答例では79°があった。
（８） 20.9％！
ア：Ａ組の最大値は30ｍ未満なのでいない。×
イ：四分位範囲＝Ｑ3（第３四分位数）－Ｑ1（第１四分位数）
箱の横の長さのことでＡ組の方が大きい。×
ウ：範囲（レンジ）＝最大値－最小値。Ｂ組の方が大きい。〇
エ：そもそも箱ひげ図というのはデータのばらつきをみるものであり、
各階級の具体的な階級値はわからない。×
オ：Ｃ組のQ3は下から27番目で25ｍ以下。ということは、25ｍ以下は最低27人はいる。〇
35人のＱ1は９番目、Ｑ2（中央値）は18番目、Ｑ3は27番目である。
ウ・オ
*誤答例ではエを選択する者がいた。
大問２（小問集合２）―44.4％
（１） 47.6％
答案では求め方も記述する。
√56＝２√14
ｎが14であれば根号がとれる。
ｎ＝14
（２） 58.0％
答案では求め方も記述する。
〔少なくとも１枚が奇数＝全体－２枚とも偶数〕
全体は、6Ｃ2＝15通り
３枚の偶数から２枚を選ぶ→3Ｃ1＝３通り
その確率は３/15＝１/５
少なくとも１枚が奇数である確率は、１－１/５＝４/５
（３） 24.3％！
ＰＱ＋ＱＢ＝ＡＢとなるには、ＡＱ＝ＰＱになればいい。
ＡＰの垂直二等分線はＡとＰから等距離にある点の集合なので、
これとＡＢとの交点がＱとなる。
*誤答例ではＰからＡＢに引いた垂線とＡＢとの交点をＱとしたもの。
大問３（関数）―34.0％
（１） 40.9％
ｙ＝ａｘ2に（ｘ、ｙ）＝（14、49）を代入する。
49＝196ａ
ａ＝１/４
ｙ＝１/４ｘ2
（２） 52.3％
横軸が時間で縦軸が距離⇒速さは傾きで表される。
傾き（変化の割合）＝ｙの増加量÷ｘの増加量
（91－49）÷（20－14）＝毎秒７ｍ
（３） 28.5％！
答案では求め方も記述する。
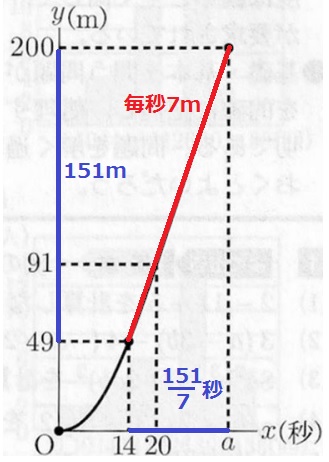
49～200ｍ地点までの距離は、200－49＝151ｍ
時間は、151÷７＝151/７秒
ａ＝14＋151/７＝249/７
（４） 16.9％！
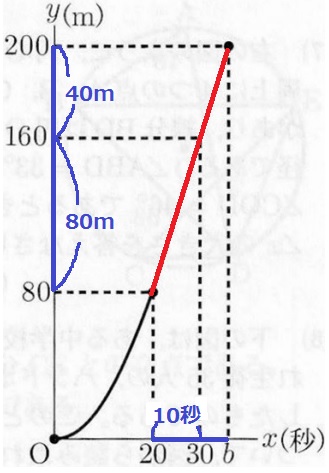
ボートＢでも同じことをする。
直線部分は10秒で80ｍなので、120ｍでは10×120/80＝15秒
ｂ＝20＋15＝35
ボートＡは249/７＝35・４/７秒。
ボートＢは35秒。
Ｂの方が先にゴールし、その差は４/７秒。
ア…Ｂ、イ…Ａ、ウ…４/７
大問４（平面図形）―38.3％
（１）ア 95.9％
９×16＝144ｃｍ2
イ…84.3％
144の正の平方根は12ｃｍ。
（２） 72.7％
縦９×横16の長方形を１辺12の正方形に変えた。
左図より青線は９ｃｍ→右図で求めたい長方形の横は12－９＝３ｃｍ
右図より赤線は３ｃｍ→左図で求めたい長方形の縦は４－３＝１ｃｍ
最も小さい長方形は、１×３＝３ｃｍ2
（３） 47.4％
△ＰＱＲ∽△ＨＱＰの証明。
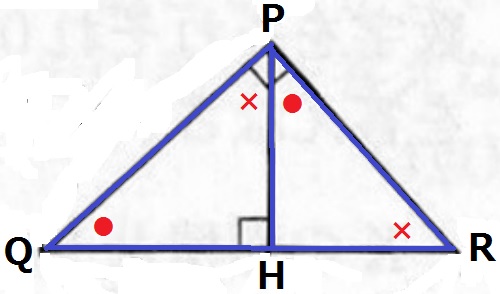
直角三角形の頻出の相似。
●＋×＝90°で等角を示すと、２角が等しいので∽。
（４） 34.3％
前問の△ＰＱＲ∽△ＨＱＰを用いる。
【ＰＱ：ＱＲ＝ＨＱ：ＱＰ】
ｘ：16＝９：ｘ
外項と内項の積で、ｘ2＝144
ｘ＞０だから、ｘ＝12（12ｃｍ）
*誤答例は９√２。△ＨＱＰは直角二等辺ではない。
（５） 5.5％!!
ＰＱ＝ＥＲの証明。
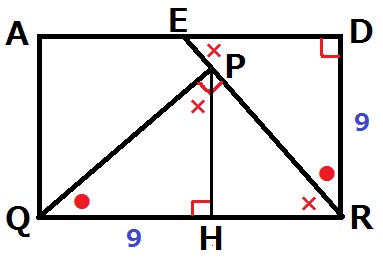
ＰＱとＥＲを１辺とする合同な三角形を探す。
ＥＲは直角三角形ＤＲＥの斜辺なので、ＰＱを斜辺とする直角三角形は、
前問の直角三角形ＨＱＰ。図７にＨを再現する。
●＋×＝90°の角度調査とＱＨ＝ＲＤ＝９ｃｍから、
１辺と両端角が等しいので△ＨＱＰ≡△ＤＲＥ。
対応する辺でＰＱ＝ＥＲとなる。
＠別解＠
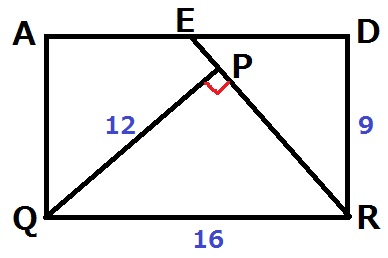
ＥＲを直接求めにいっても良いと思う。
ＥＱに補助線。
△ＥＱＲを２通りの方法で算出すると、
【ＱＲ×ＤＲ÷２＝ＥＲ×ＰＱ÷２】
16×９÷２＝ＥＲ×12÷２
ＥＲ＝16×９÷12＝12ｃｍ
ＰＱ＝ＥＲ＝12ｃｍ
＠余談＠
リード文の最後を図示すると、このように場所を入れ替えれば１辺12ｃｍの正方形になる。
大問５（空間図形）―17.7％
（１） 40.3％
正方形の対角線ＡＣとＢＤの交点をＲとする。
Ｒは正方形ＡＢＣＤの中心でＯの真下にあり、ＯＲが正四角錐の高さにあたる。
直角二等辺三角形ＡＢＣの辺の比は１：１：√２→ＡＣ＝４√２ｃｍ
正方形の対角線はおのおのを２等分するので、ＡＲ＝４√２÷２＝２√２ｃｍ
△ＯＡＲで三平方→ＯＲ＝１ｃｍ
（２） 16.3％！
答案では求め方も記述する。
このように切り取る。
△ＯＰＱと△ＯＥＧの辺の比は①：③。
ＰＱ＝４√２×①/③＝４√２/３ｃｍ
*誤答例は２√２。
（３） 4.1％!!
答案では求め方も記述する。
面ＯＢＦＨＤで立体を分けると左右対称である。
対称性からＰＦ＝ＱＦで、△ＰＦＱは二等辺三角形。
（１）の点ＲはＯの真下、面ＯＢＦＨＤ上にある。
同様に対称性からＲはＰＱの中点である。
ＲＦは底辺ＰＱを二等分するので、二等辺三角形ＰＦＱの高さにあたる。
ＲＦは１辺２ｃｍの立方体の対角線だから、ＲＦ＝√（２2＋２2＋２2）＝２√３ｃｍ
したがって、△ＰＦＱの面積は、４√２/３×２√３÷２＝４√６/３ｃｍ2
大問１
（１）～（６）全部とる。
（７）ｘを知るにはどこがわかればいいか。直径がでてきたら90°を見つけよう。
（８）エの誤答とオの正答をしっかり理解しておく。
大問２
（２）少なくとも〇〇は余事象で攻める。
（３）思考力が試された。最初にどんな感じになるか想像してみよう。
折れ曲がったＰＱ＋ＱＢがまっすぐなＡＢになるということはＰＱ＝ＡＱである。
大問３
（１）基本だが正答率が40％。最初の放物線だけをみる。
（２）直線部分をみる。算数レベル。
（３）ここも算数で解けてしまう。
（４）ここも算数。前問と内容はほぼ同じ。
大問４
題材がおもしろい。
（２）長方形と正方形を照らし合わせ、等辺を調べていく。
（３）他県でも頻出の∽。
（５）はじめはＥＲの長さを求めました(;^ω^)
それでも証明になる。
大問５
（１）正四角錐の高さと３ｃｍを１辺とする直角三角形を作成。
（２）空間図形はどこの平面で切り取るかが勝負です。
（３）体積と高さから底面積を出す方法も考えられるが、
本問はＰＱがわかっているので、二等辺ＰＦＱの高さを知ればいい。
（１）に登場する点を活用する。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント