15.2点（22点満点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
６－（－４）÷２
＝６－（－２）
＝６＋２
＝８
エ
（２）
（３ｘ－２）/６－（２ｘ－３）/９
＝｛３（３ｘ－２）－２（２ｘ－３）｝/18
＝（９ｘ－６－４ｘ＋６）/18
＝５/18ｘ
ウ
（３）
６ｘ2÷（－３ｘｙ）2×27ｘｙ2
＝６ｘ2÷９ｘ2ｙ2×27ｘｙ2
＝18ｘ
ウ
（４）
（√５－√２）（√20＋√８） ←後半を√４でくくる
＝（√５－√２）√４（√５＋√２）
＝２（√５－√２）（√５＋√２）
＝２｛（√５）2－（√２）2｝
＝２×（５－２）
＝６
ア
（５）
（ｘ－３）2＝－ｘ＋15
ｘ2－６ｘ＋９＝－ｘ＋15
ｘ2－５ｘ－６
＝（ｘ＋１）（ｘ－６）＝０
ｘ＝－１、６
ウ
（６）
ア：ｘｙ＝100→ｙ＝100/ｘ（反比例）×
イ：ｙ＝３ｘ（比例は一次関数の仲間。切片ｂ＝０の一次関数が比例）〇
ウ：ｙ＝πｘ2（ｙ＝ａｘ2）×
エ：ｙ＝ｘ3×！
イ
（７）
４枚から３枚を選び、順番をつけて並べる→4Ｐ3＝４×３×２＝24通り
213以上の並びを数える。２つの１は別に扱うこと！
２１３（２１３）
２３１（２３１）
３１１（３１１）
３１２（３１２）
３２１（３２１）
計10通り。
確率は、10/24＝５/12
ウ
（８）
偶奇判定。反例を探す。
ア：ｎ－２⇒ｎが偶数だと、（偶数ｎ）－（偶数２）＝（偶数）×
イ：４ｎ＋５⇒４ｎはｎに偶数４をかけるので必ず偶数。
（偶数４ｎ）＋（奇数５）＝（奇数）〇
ウ：３ｎ⇒ｎが偶数だと、（奇数３）×（偶数ｎ）＝（偶数）×
エ：ｎ2－１⇒ｎが奇数だと、（奇数ｎ2）－（奇数１）＝（偶数）×
イ
（９）
ｙ＝ａｘ2において、ｘの値がｐ→ｑに増加したときの変化の割合はａ（ｐ＋ｑ）。
変化の割合は２×（１＋３）＝８
一次関数の変化の割合は傾きａで表されるから、ｙ＝８ｘ＋６
エ
（10）
ア：異なる２点を結ぶと直線になる。１直線を含む平面はクルクル回せるので決まらない。×
イ：交わる２直線を含む平面は動かせないので１つに決まる。〇
ウ：平行な２直線でも同様に動かせず、１つに決まる。〇
エ：同じ直線上にある３点→１直線と同じでクルクル回せて決まらない。×
イ・ウ
大問２（小問集合２）
（１）
ア：範囲（レンジ）＝最大値－最小値。Ｂ組の方が大きい。×
イ：四分位範囲＝Ｑ3（第３四分位数）－Ｑ1（第１四分位数）
Ａ組…30－15＝15ｍ、Ｂ組…35－20＝15ｍで同じ値。〇
ウ：中央値（第２四分位数；Ｑ2）はともに25ｍ。〇
エ：32人を４等分すると、Ｑ3は上から８番目と９番目の平均。
Ｂ組の35ｍ以上は少なくとも８人いる。Q3が30ｍのＡ組はこれより多いと確実にいえない。×
オ：25ｍ以上はＡ組、Ｂ組ともに少なくとも16人以上はいる。
たとえば、Ａ組に25ｍが複数人いて、上から17番目や18番目も25ｍかもしれないので、
25ｍ以上が同数とは限らない。×
イ・ウ
（２）
△ＡＢＣ≡△ＥＡＤの証明。
仮定より、ＡＢ＝ＥＡ
平行四辺形の対辺は等しいから、ＢＣ＝ＡＤ
二等辺ＡＢＥの底角とＡＤ//ＢＣの錯角で、∠ＡＢＣ＝∠ＡＥＢ＝∠ＥＡＤ
２辺とあいだの角が等しいので合同。
Ⅰ…オ、Ⅱ…ク
（３）①
６秒後にＰは６ｃｍ移動している。
Ｄを折り返してＡＤの中点にくる。ｙ＝２
ウ
②
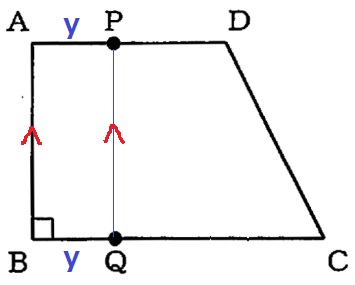
ＰとＱはそれぞれ別の場所を動くが、ＡＢ//ＰＱとなるにはＡＰ＝ＢＱ、
つまり、ＢＱの長さがｙになればいい。
グラフにＡとＢのグラフを記す。
Ａは原点Ｏから４秒ごと、Ｂは（０、６）から３秒ごとに向こう側に着く。
ｙの値が等しくなる交点は４回。
エ
大問３（図形）
（１）
ＡＢに補助線。半径より△ＯＡＢは二等辺三角形。
∠ＯＢＡ＝（180－48）÷２＝66°
ＡＯ//ＢＣの錯角で∠ＯＢＣ＝48°
∠ＡＢＣ＝66＋48＝114°
円に内接する四角形の対角の和は180°なので、
∠ＡＤＣ＝180－114＝66°
（２）①
ＦＥ//ＤＢより、ＡＥ：ＥＢ＝ＡＦ：ＦＤ＝１：１
ＡＦ＝10÷２＝５ｃｍ
△ＡＥＦで三平方→ＦＥ＝√34ｃｍ
②
△ＢＣＨ∽△ＤＦＨで、ＢＨ：ＨＤ＝②：①
△ＡＥＦ∽△ＡＢＤで、ＥＦ＝③÷２＝〇1.5
比を整理すると、ＥＦ：ＢＨ：ＨＤ＝〇1.5：②：①＝３：４：２
△ＥＦＧ∽△ＤＨＧより、ＦＧ：ＧＨ＝３：２
先ほどの△ＢＣＨ∽△ＤＦＨから、ＦＨ：ＨＣ＝①：②
方針；【△ＤＦＣ⇒△ＤＦＨ⇒△ＤＧＨ】
５×６÷２×①/③×２/５＝２ｃｍ2
（３）①
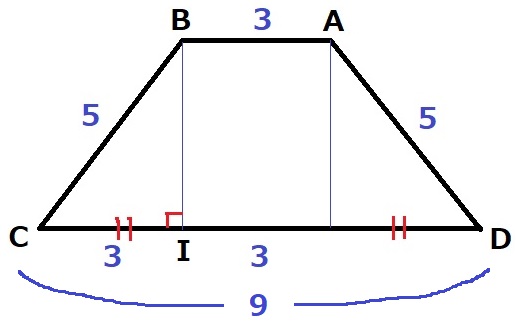
四角形ＡＢＣＤは等脚台形で左右対称。
２本の垂線を引き、３ｃｍを下に平行移動させる。
Ｂを通る垂線の足をＩとすると、ＣＩ＝（９－３）÷２＝３ｃｍ
△ＢＣＩは３：４：５の直角三角形→ＢＩ＝４ｃｍ
台形ＡＢＣＤの面積は、（３＋９）×４÷２＝24ｃｍ2
②
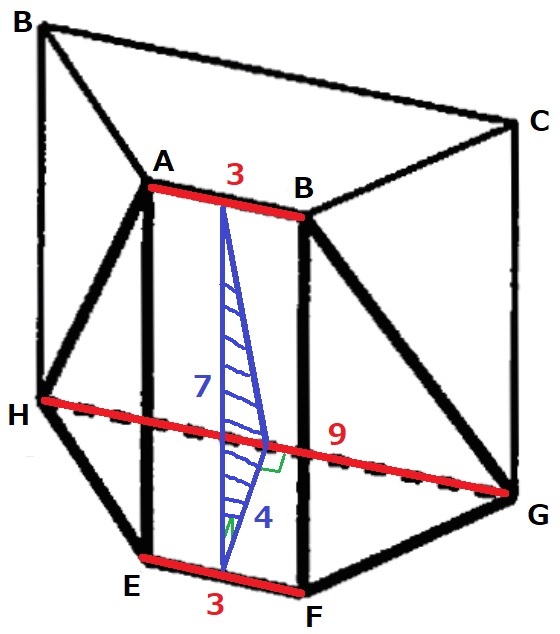
断頭三角柱の考えを用いる。
求める立体を対称的に真っ二つに切断する。
断面積は、４×７÷２＝14ｃｍ2
高さの平均は、（ＡＢ＋ＥＦ＋ＨＧ）÷３＝（３＋３＋９）÷３＝５ｃｍ
よって、求積すべき立体の体積は、14×５＝70ｃｍ3
今年からＡグループ・Ｂグループの区別がなくなった。
形式や問題数に変更はなさそうだが、中身はさらに易化している。
大問１
配点率が45％もある。基本問題がほとんど。
（４）√４を外に出しておく。
（７）２つある１を区別して扱う。
（８）具体的な数字をあててしまっても良い。
（10）山形もこういう小問を出題してくる。
大問２
（１）四分位数からは『少なくとも何人は〇〇』としかいえない。
同じ記録を持つ者が複数いるパターンを想像する。
（２）証明も楽だった。記述式でも解けるようにしたいレベル。
（３）②これみよがしに提示されたグラフを使う。
座標もご丁寧にｘ＝12、ｙ＝６で止まっている(´ﾟωﾟ)oh…
大問３
（１）円周角の定理でもＯＫ。
（２）②面積比で算出できるので、前問の利用がなかった。
ＦＥ//ＤＢからＧＨを１辺とする△ＤＨＧと△ＥＦＧの相似に気がつきたい。
（３） ①等脚台形は公立高校入試の世界でいたるところに出てくる。
②断頭三角柱はテクニックとして覚えておくと応用が利く。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント