平均51.9点(前年比;+4.9点)

問題はこちら→千葉日報さん
大問1(小問集合)-64.9%
(1)① 95.7%
-4+12÷2
=-4+6
=2
② 76.6%
a2b÷3ab×(-9a)
=-3a2
③ 70.8%
(√7+√3)(√7-2√3)
=7-2√21+√21-6
=1-√21
(2)① 84.8%
x2+2x=5
x2+2x-5=0
ウ
② 66.8%
解の公式を適用する。xの係数が偶数なので、b=2b’が使える。
x=-1±√6
あ…-、い…1、う…6
(3)① 68.6%
全数調査は調査対象すべてを調べ上げる。
標本調査は母集団のなかから標本を無作為に抽出して、母集団の様子を推し量る。
ア:総務省統計局が5年に1度行う国勢調査は全数調査の代表例。
国の基礎的な統計資料として国策の判断に使われる。
ウ:健康診断も個々人のデータをとらなければ意味がないので全数調査。
エ:進路希望調査も同様。
@@
イ:水質調査はすべての川の水を調べ上げるのは不可能なので標本調査を行う。
イ
@テレビの視聴率@
標本(サンプル)の大きさはどの程度求められるか。
大学レベルの統計学の知識が求められると思うのでサボにはわかりませんが、視聴率を計測する機器が設置されているテレビの台数は、全体の0.01%にも満たないようです。
視聴率調査に協力している人を全く見掛けない理由(ねとらぼ)
↑この記事によると、2017年10月時点で調査対象世帯は全体の0.00005%以下となっている…。
それだけで残りの99.999…%以上を推し量って良いものなのか疑問に思われますが、統計学的には十分信頼するに足りるサンプル数なんだとか。どうやら母集団が大きくなるほど、標本の大きさは思ったより小さくても間に合うようです。反対に母集団が小さいと(例えば1クラス内の動向では)多くの標本をとらなければならない。
② 70.2%
抽出した10個のうち、オレンジ:白=③:⑦
オレンジは全体で30個だから、白の全体は、30×⑦/③=70個
え…7、お…0
(4)① 93.4%

どこかを底面に見立てて組み立てればいい。
もしくは、4つの面がストレートに並ぶところを側面とすると、
エの残り2面は天井と床に分かれず、かぶってしまう。
エ
② 51.9%

最短距離なので展開する。AHは3面をまたぐ。
辺の比は3:9=①:③→三平方で〇√10
AH=3×〇√10=3√10cm
か…3、き…1、く…0
(5)① 78.2%
全体は6×6=36通り
y=x上にある→xとyの値が同じ。
(1、1)~(6、6)のゾロ目を出す。6通り
確率は、6/36=1/6
け…1、こ…6
② 30.8%!

半径4cmの円を描く。
軸上はx=0かy=0だから含まない。
4cm『以下』なので円周上も含むが、該当する点はない。
上図の8通りで、確率は8/36=2/9
さ…2、し…9
(6)① 88.6%

弧BCの円周角より、x=∠BDC=63°
す…6、せ…3
② 38.9%

△EBDの外角定理で、∠EBD=63-38=25°

△ABFで外角定理→y=63+25=88°
そ…8、た…8
(7)① 41.1%
円錐の扇形の中心角が90°であることに着目する。
側面の扇形の中心角:底面の円の中心角=90:360=1:4
側面の扇形の半径(母線):底面の円の半径は逆比で4:1。
側面の扇形の半径は、底面の円の半径の4倍である。
ち…4
② 16.8%!(無答35.8%)

扇形の中心をBとすると、接点はAだから中心Oは半直線BA上にある。
底面の円の半径はABの4分の1の長さ。
ABの垂直二等分線で半分、さらに半分にした点をCとするとACが円の半径。
Aに対してCを反対側にもってきた点がOである。
①半直線BAをひく。
②垂直二等分線を2回行い、ABの4分の1であるACをつくる。
③AからCまでの長さをとり、Cを反対側に移動させる。①との交点がO
大問2(関数)-45.4%
(1)① 80.0%

y=1/2x2にx=3を代入。
y=1/2×32=9/2
つ…9、て…2
② 44.6%
Qはy軸についてPと対称→Q(-3、9/2)
平行四辺形の対辺は等しいから、QP=SR=6
Rのx座標は6、これをy=1/2x2に代入してR(6、18)
Q(-3、9/2)→R(6、18)
傾き=変化の割合=yの増加量÷xの増加量
=(18-9/2)÷{6-(-3)}=27/2÷9=3/2
y=3/2x+bに(6、18)を代入する。
18=3/2×6+b
b=9
と…3、な…2、に…9
(2) 11.5%!(無答42.7%)

P(p、1/2p2)とする。
PQ=2p→Rのx座標は2pだから、y=1/2x2に代入してy座標は2p2。
SH=2p2-1/2p2=3/2p2
3/2p2=2p×2
3/2p2-4p=0
3p2-8p
=p(3p-8)=0
p>0より、p=8/3
ぬ…8、ね…3
@余談@
本問は方程式で解いた方が速いですが、最近ここらで裏設定を見かけるので調べてみました。
興味のある方はご覧ください。

(1)OPの傾きは3/2なので、QRとOPは平行です。
(2)SH=2PQより、SH=4QH
QH=①とすると、SH=④
切片をTとすると、△TQH:△TRS=TH:ST=1:2→TH=④×1/3=〇4/3
QTの傾きは4/3→OP;y=4/3x
Pはy=1/2x2とy=4/3xの交点なので、
1/2x2=4/3x
x(1/2x-4/3)=0
x>0だから、x=8/3
大問3(平面図形)-35.2%
(1) 88.3%
△EBCの内角より、∠ECB=180-(90+45)=45°
∠EBC=∠ECB=45°だから、△EBCは直角二等辺三角形。
よって、EB=EC
a…イ、b…ウ、c…カ
(2)6点-11.7%!、3点-5.3%、無答-29.4%
△EBF≡△ECAの証明。
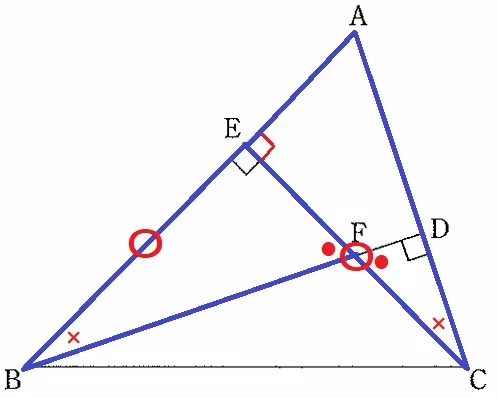
∠BEF=∠CEA=90°
EB=EC
△EBFの内角で∠EFB=●、∠EBF=×とする。●+×=90°
対頂角で、∠DFC=●
△DCFの内角より、∠DCF=180-(90+●)=×
よって、∠EBF=∠ECA
1辺と両端角が等しいので合同。
@別解@

∠BEC=∠BDC=90°に注目して、円周角の定理の逆からBCを直径とする円を描き、
弧EDに対する円周角から、∠EBF=∠ECAを指摘できる。
(3) 5.7%!!(無答42.7%)
難問です(;´・ω・)
初手でミスると迷子になる。
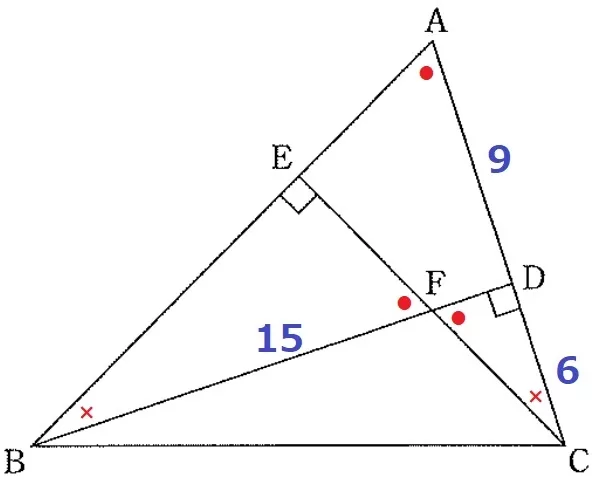
どこかで相似を使いたいが、BFが浮いている。
問題文ではAC=15cmではなく、わざわざAD=9cm、DC=6cmと分けている。
ADとDCを1辺とする三角形に着目し、BFとACの間にあるFDをxとおくと…

△ABD∽△FCDが使える!
AD:DB=FD:DC
9:(15+x)=x:6
内項と外項の積から、x(15+x)=54
x2+15x-54
=(x+18)(x-3)=0
x>0より、x=3

△DCFで三平方→FC=3√5
△DCF∽△EBFより、相似比は15:3√5=5:√5
面積比は2乗して⑤:①なので、△EBFの面積は、3×6÷2×⑤=45cm2
の…4、は…5
@余談@
実は12年前のラス問に似た構図が出ています。

2012年千葉前期数学(大問5-3)より。
ホワイトボード時代の解説です(;´∀`)
正答率は資料損失により不明ですが、相当低かったと思われます。
@別解@
寄せられたコメントによると、Eから2本の垂線を引く方法があるようです。
私なりの解法を考えてみました。

Eから垂線をひき、BD、ACとの交点をP、Qとします。
(2)△EBF≡△ECAより、対応するFB=ACを底辺と見立てると、
高さにあたるEP=EQがいえます。
四角形EPDQは4つの角が直角で、隣り合う辺が等しいから正方形です。
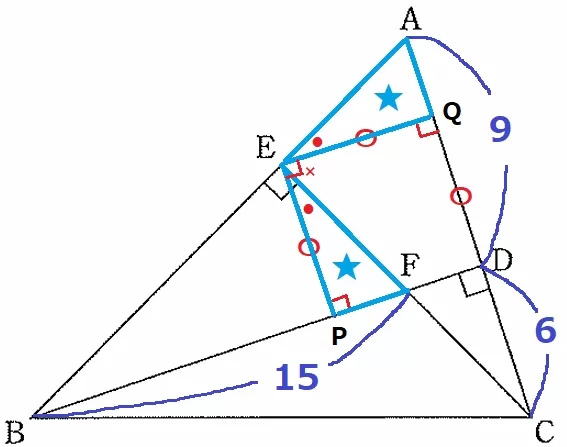
EP=EQ、∠EPF=∠EQA=90°
●+×=90°で角度を移すと、∠FEP=∠AEQ
1辺と両端角が等しく、△FEP≡△AEQ
対応する辺から、FP=AQ
ということは、AQ+QD=FP+PE=9cm
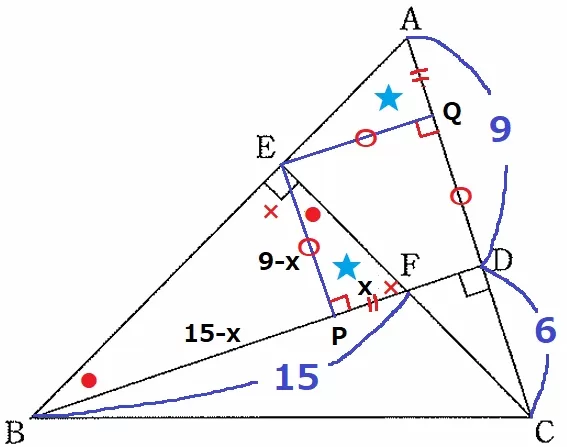
同様に●+×=90°を使うと、二角相等で△FEP∽△EBP
最も短いFP=xとすると、PE=9-x
PB=15-x
FP:PE=EP:PB
x:(9-x)=(9-x):(15-x)
内項と外項の積で、(9-x)2=x(15-x)
x2-18x+81=15x-x2
2x2-33x+81
=(2x-27)(x-3)=0
x<9より、x=3
EP=9-3=6cm
したがって、△EBFの面積は、15×6÷2=45cm2
大問4(方程式)-30.6%
(1)① 89.7%

△OAB∽△OPQ、相似比は高さの比からOM:ON=1:2
PQはABの2倍。
ひ…2
② 33.4%
今度はPQ=4ABにしたい。
OM:ON=1:4→OM:MN=1:3
ふ…1、へ…3
③ 47.6%

OPの格子点に注目すると、右に4、上に1だから傾きは1/4。
OPは原点を通る比例→y=1/4x
x=10を代入して、y=1/4×10=5/2
ほ…5、ま…2
(2)a-4.7%!!(無答54.9%)、b-5.0%!!(無答57.7%)
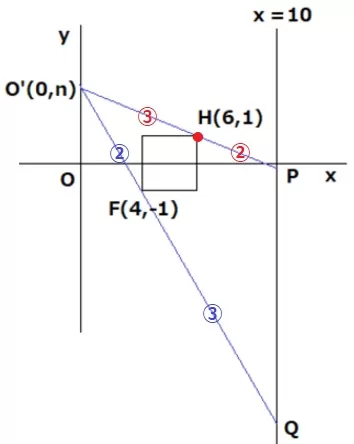
O’H:O’P=6:4=③:⑤
O’とHのy座標の差はn-1。
O’とPのy座標の差は、(n-1)×⑤/③=5/3n-5/3
Pのy座標p=n-(5/3n-5/3)=-2/3n+5/3
O’F:O’Q=②:⑤
同様に、O’とQのy座標の差は、(n+1)×⑤/②=5/2n+5/2
Qのy座標q=n-(5/2n+5/2)=-3/2n-5/2
a…p=-2/3n+5/3、b…q=-3/2n-5/2
(3) 3.1%!!(無答51.0%)
PQ=p-q
=(-2/3n+5/3)-(-3/2n-5/2)
=-2/3n+5/3+3/2n+5/2
=5/6n+25/6=100 ←6倍
5n+25=600
n=115
み…1、む…1、め…5
●講評●
基本問題が多いが、難問は落差がすごい。
大問1
前半は基本。点を稼いでおこう。
(4)①展開図は小学生でも解けます(`ω´)
(5)②半径4mの円を描く。格子点がありがたい。
(6)②外角定理を切り替えて適用する。
(7)①母線:円の半径の関係性は理解しておきたい。
②Aでくっつくので、扇形の中心からA方向に伸ばした直線上にある。
前問をヒントに母線の4分の1の距離をAからつくる。
大問2
(2)心なしか公立高校入試の世界で、平行四辺形を使った関数の問題をよく見かける。
各座標を文字で示し、方程式に落とし込む。
大問3
(2)直角を利用して等角を指摘する。
(3)最大の難所。図がシンプル過ぎて、アプローチを誤ると迷宮入りになる。
文字を2種類設定して三平方→連立を駆使すると高次式があらわれて号泣。
問題文の情報からADとDCをそれぞれ1辺とする三角形に絞る。
BF=15が宙に浮いているので、FDに文字を設定して接続すると相似が使える。
作問者の性格なのか、千葉では内項外項の積にもっていくパターンが見受けられる。
対策してたかどうかで差がでるが、不正解でも合否に大きな影響はない。
大問4
(1)②1:4なのはOM:ON。
(2)3:2、2:3と比が逆になる。
y座標の差を求め、nから引く。計算力勝負。
(3)前問ができれば取りやすい。PQの長さ=Pのy座標-Qのy座標
@2024年度・千葉解説@
社会…平均57.5点 理科…平均59.1点 英語…平均56.4点 国語…準備中
思考力を問う問題…数学と英語のみ。来年度の実施校は千葉・千葉東・東葛飾。


コメント
第3問(3)
点Eから辺BD及び辺ACに垂線下ろした足を
P,Q
直線EPの延長に点Cから垂線を下ろした足をR
とすると、
EP=EQ=QDより、四角形EQDPは正方形であることがわかります。
加えて、ED//DCより
△DPCは直角二等辺三角形故、
EP=DP=DC=6cm
∴△BEF=45cm^2
とも出せました。
コメントありがとうございます。
面白い補助線ですね!
前問の合同→等積から、底辺を15としたとき高さのEP=EQより正方形になりますね。
ED//PC?かと思われますが、ここはどうでしょうか。
2本の垂線をヒントにサボなりの解法をあげてみました。
このような感じでいかがでしょうか。
他県では相似のパターンがほぼ見たことあるような形で正直暗記でどうにかなってしまうのですが、千葉県は見たことがない相似の問題を作るのが上手いですね。こうした暗記ばかりでない思考力を求めているのかもしれませんね。
コメントありがとうございます。
作問が絶妙ですよね。幾何に強い中受生も敗北しそうな難問で、歯がゆいながらも解法が見つかると感嘆しました。
一体、どんな方が作っているのか興味あります。
こんばんは。今回は、2024千葉県公立高校数学入試問題の大問3の(3)の[一部改良型]の解法を考えてみました。前半は、サボ先生の解法と同じです。よって、FD=3であります。後半は、△ABCから△FBCを引くと、2つの合同な直角三角形が残るので、それを2で割って、求めてみました。
[一部改良型](前半)
△ABD∽△FCDより、AD:DB=FD:DC
9:(15+x)=x:6 x(15+x)=54
x²+15x−54=0 (x−3)(x+18)=0
x>0より、x=3 ここまでは、サボ先生の解法と同じです。
(後半)△FBCの面積は15✕6÷2=45cm²。
△ABCの面積は15✕(15+3)÷2=15✕18÷2=135cm²。△EBFの面積は、△AECと△FEBは合同なので、△ABCから△FBCを引いて2で割ればよい。
△EBF=(135−45)÷2=45cm²である。よって、答えは、の‥4、は‥5である。
以上ですが、後半は、相似の関係は使わずに、三角形の面積のみで解いてみました。ご確認いただけますと嬉しく思います。
このように解法の糸口を探りながら、考えを深める事もとても大切かと思い、投稿しました。あまりオススメの解法ではありませんが、受検生や来年度の受検生の参考になればと思います。これからも宜しくお願いします。お助けマンより。
相似を経由しなくてもいけますね。良い解法だと思います。
申し訳ございませんが、諸事情により数日間ブログの更新が落ち気味になります。
コメントありがとうございました。 サボ