2022年度　山形県公立高校入試問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　95.7％
－７－（－２）－１
＝－７＋２－１
＝－６

②　85.9％
－３/４÷６/５＋１/２
＝－５/８＋１/２
＝－１/８

③　84.7％
（－６ｘｙ²＋８ｘｙ）÷（－２ｘｙ）
＝－６ｘｙ²÷（－２ｘｙ）＋８ｘｙ÷（－２ｘｙ）
＝３ｙ－４

④　71.4％
（２－√６）²＋√24
＝４－４√６＋６＋２√６
＝10－２√６

（２）　80.8％
答案では解き方も書く。
（３ｘ＋１）（ｘ－２）＝ｘ－１
３ｘ²－５ｘ－２＝ｘ－１
３ｘ²－６ｘ－１＝０
解の公式を適用。ｘの係数が偶数なので、ｂ＝２ｂ’が使える。
ｘ＝（３±２√３）/３

（３）　60.8％
５枚から１枚取り、それを戻さずにもう１枚取る
→５枚から同時に２枚取るのと同じ、₅Ｃ₂＝10通り

余りが１となるには差が１である組み合わせに着目する。
（５、４）（４、３）（３、２）
ただし、（２、１）は割る数が１なので余りなし！
他には（５、２）がある。
計４通り。
確率は、４/10＝２/５

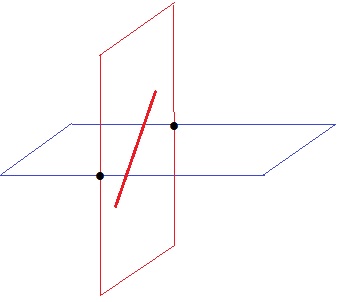
（４）　41.2％
反例を挙げればいい。
ア

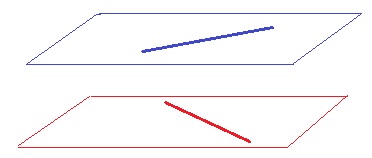
平面が平行でも直線が平行とは限らない。

イ

面が交わっても、直線が交わらずに平行である場合がある。

ウ

平面が垂直でも、平面と直線が垂直とは限らない。

エ

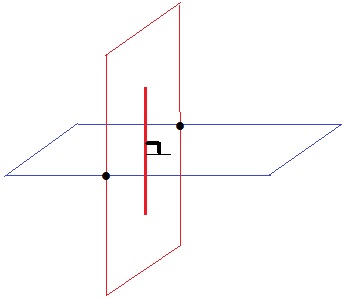
平面と直線が垂直の場合、２つの平面は必ず垂直になる。
エ

（５）　47.1％
最頻値（モード）は最もあらわれている値で１点。エが外れる。
42個の中央値（メジアン）は21番目と22番目の平均で１点。
30個の中央値は15番目と16番目の平均。イが外れる。

０点の割合を比較する。
昨年…12/42＝２/７
ア…７/30
ウ…９/30
210で通分して比較すると、０点の割合が最も小さいのはア。
１点以上の割合は今年の方が大きいのでアとなる。

大問２（小問集合２）

（１）①　56.1％
ｙ＝ａｘ²においてｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
１/２（－４＋０）＝－２

②　26.7％！
ｙ＝１/２ｘ²にｘ＝２を代入して、Ａ（２、２）
反比例の比例定数は積ｘｙで一定。
反比例のグラフ②はｙ＝４/ｘ

Ｂのｘ座標とｙ座標がともに負の整数⇒格子点を探す。
（－１、－４）（－２、－２）（－４、－１）
図の雰囲気からして（－１、－４）っぽいが(;`ω´)
ｙ＝ａｘ²は上に凸のグラフで、ａ＜０の負の整数に当てはまるものを絞ると、
（－１、－４）→ａ＝－４
（－２、－２）→ａ＝－１/２
（－４、－１）→ａ＝－１/16
したがって、ａ＝－４

（２）　80.8％

①直線ＡＰ⊥直線ℓ→Ａを通る垂線
②Ｐを中心としてＢを回転移動させるとＣと重なる
→ＢＰ＝ＣＰを半径とする円の円周上にＢとＣがある→ＢＣの垂直二等分線
これらの交点がＰである。

（３）①　84.7％
●１次方程式の場合
Ａ地区の面積をｘｋｍ²とすると、Ｂ地区の面積は（630－ｘ）ｋｍ²
70％＝0.7、90％＝0.9
森林面積の合計で等式。
0.7ｘ＋0.9（630－ｘ）＝519

●連立方程式の場合
Ａ地区の面積をｘｋｍ²、Ｂ地区の面積をｙｋｍ²として、
ｘ＋ｙ＝630
0.7ｘ＋0.9ｙ＝519

②　39.6％
先の方程式を解く。
ｘ＝240
Ａ地区の面積が240ｋｍ²なので、Ａ地区の森林面積は、
240×70％＝168ｋｍ²

（４）100％―29.0％！、50～99％―25.5％、１～49％―21.2％
説明問題。
〔３の倍数＋１〕を証明したいので、３（　）＋１の形に持っていく。

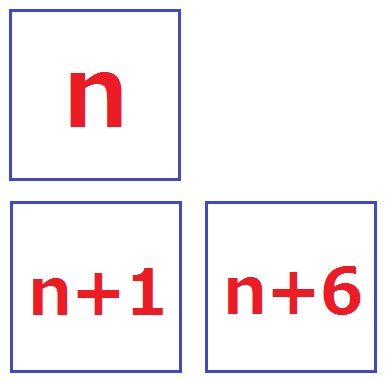
Ｌ字に並んだ３つの自然数の和は、
ｎ＋（ｎ＋１）＋（ｎ＋６）
＝３ｎ＋７
＝３（ｎ＋２）＋１
ｎ＋２は整数だから、３（ｎ＋２）＋１は３の倍数に１を加えた数である。

大問３（数量変化）

（１）①　75.7％
ｘ＝３のとき、ＰはＡＥ上にある。
底面は長方形ＥＦＧＨ、高さはＰＥ＝１ｃｍの四角錘。
３×５×１÷３＝５

②ア…58.4％、イ…78.8％、ウ…49.4％、グラフ…86.7％

◆０≦ｘ≦４のとき
ＰはＡＥ上にある。
底面積は変わらず、高さが減少する⇒体積は一次関数で減少。
ｘ＝０のとき、ｙ＝３×５×４÷３＝20（切片）
20ｃｍ³が４秒で０ｃｍ³になるので、変化の割合は－20÷４＝－５
ｙ＝－５ｘ＋20

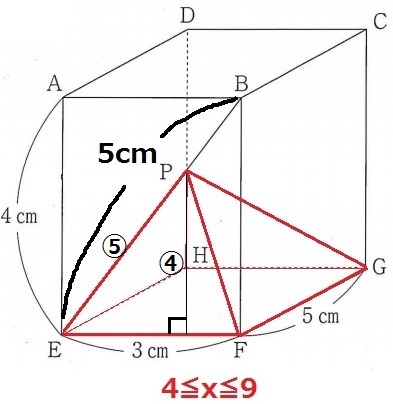
◆４≦ｘ≦９のとき
ＰはＥＢ上にある。
（△ＡＢＥは３：４：５の直角三角形→ＥＢ＝５ｃｍ）
底面積は変わらず、高さが増加する⇒体積は一次関数で増加。
ＥＰの長さを⑤とすると、高さは相似で④に相当する。
０≦ｘ≦４の変化率が－５だった。
増加だから＋に転じて、体積の変化率は＋５×④/⑤＝＋４（傾きは４）
ｘ＝９、すなわち、ＰがＢにくるとき、体積ｙは20に戻るので、
ｙ＝４ｘ＋ｂに（ｘ、ｙ）＝（９、20）を代入。
20＝４×９＋ｂ
ｂ＝－16
ｙ＝４ｘ－16

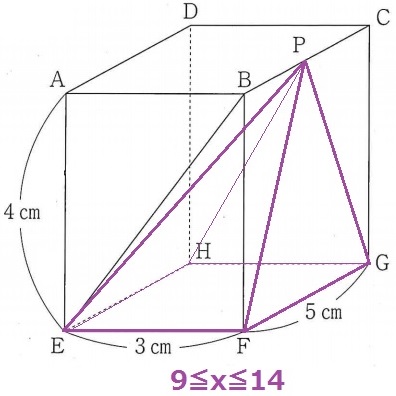
◆９≦ｙ≦14のとき
ＰはＢＣ上にある。
底面積も高さも変わらない。等積変形で体積は20ｃｍ³で一定。

まとめるとこうなる。
ア…ｙ＝－５ｘ＋20、イ…９、ウ…ｙ＝４ｘ－16

（２）　13.3％！
出題の仕方が妙(´ﾟдﾟ｀)
わかるところから、ひも解いていく。

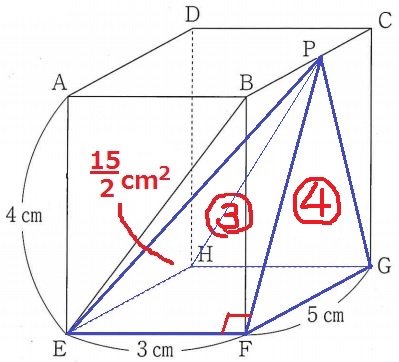
△ＰＥＦの面積は△ＰＦＧの３/４倍。
５×４÷２×③/④＝15/２ｃｍ²

Ｐが移動したＢＰの長さが知りたい。
そこでＰＦに注目する。
ＢＦ＝４ｃｍなので、ＰＦがわかれば△ＢＰＦの三平方からＢＰが出る。

ポイントはＥＦ⊥ＰＦ
側面の長方形の内角より、ＥＦ⊥面ＢＦＧＣ
ＰＦは面ＢＦＧＣ上の線分でＥＦとはＦで交わるからＥＦ⊥ＰＦがいえる。
ＰＦ＝15/２×２÷３＝５ｃｍ

△ＢＰＦも３：４：５の直角三角形→ＢＰ＝３ｃｍ
ＰがＢに着くのは９秒後でＰは毎秒１ｃｍだから、答えは９＋３＝12秒後

大問４（平面図形）

（１）100％―20.4％！、50～99％―11.8％、１～49％―34.5％
△ＡＢＣ∽△ＡＨＥの証明。

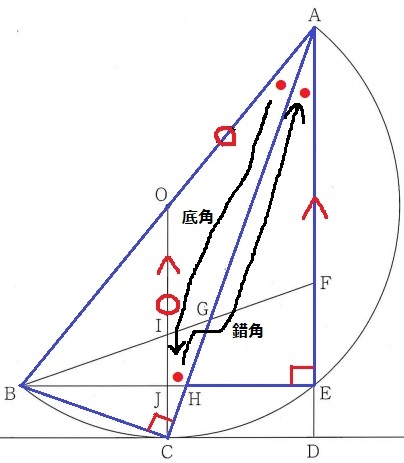
半円の弧に対する円周角で、∠ＡＣＢ＝∠ＡＥＨ
半径よりＯＡ＝ＯＣ、△ＯＣＡは二等辺で底角が等しい。
ＯＣ//ＡＤの錯角と合わせて、∠ＢＡＣ＝∠ＨＡＥ
２角が等しく∽。

（２）①　14.1％！

先ほどの△ＡＢＣ∽△ＡＨＥをさらに展開する。
△ＡＨＥと△ＢＣＪにおいて、
弧ＣＥに対する円周角で∠ＨＡＥ＝∠ＣＢＪ
同位角より、∠ＡＥＨ＝∠ＯＪＢ＝90°
反対側の角である∠ＢＪＣ＝90°
２角相等で△ＡＢＣ∽△ＡＨＥ∽△ＢＣＪが導ける。
ＡＢ：ＢＣ＝ＢＣ：ＣＪ
ＣＪ＝３×３/９＝１ｃｍ

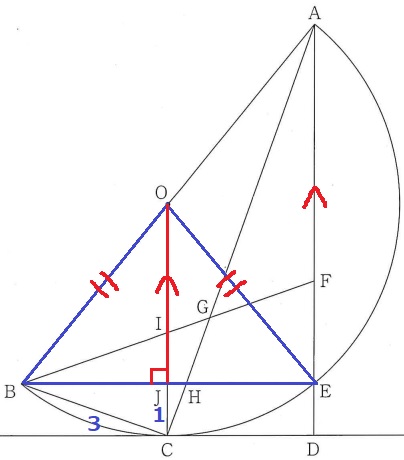
なんとなくＢＪとＪＥが同じっぽい。。
ＯＥに補助線をひく。半径から△ＯＢＥは二等辺。
頂角Ｏから底辺ＢＥにおろした垂線ＯＪは二等辺を左右に二等分する。
ＯＪを対称の軸として左右対称であり、ＢとＥは対応する位置にある。

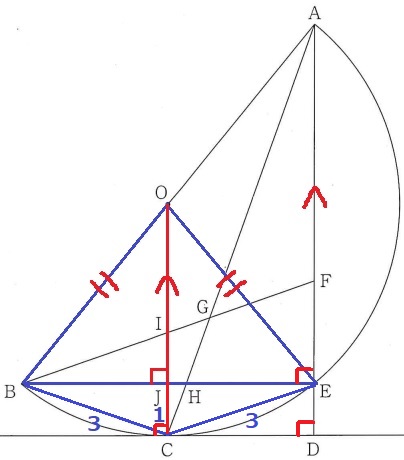
ＡＪの延長線上にあるＣについても同様のことがいえる。
ＥＣに補助線。
ＥＣ＝ＢＣ＝３ｃｍ
△ＪＣＥで三平方→ＪＥ＝２√２ｃｍ

半径ＯＣと接線は直交し、円周角や同位角を合わせると、
四角形ＪＣＤＥの内角はすべて90°で長方形。
ＣＤ＝ＪＥ＝２√２ｃｍ

②　0.8％!!!

ＢＥ＝２√２×２＝４√２ｃｍ
△ＡＢＥで三平方→ＡＥ＝７ｃｍ
ＡＤ＝７＋１＝８ｃｍ
これを⑤：③に案分して、ＡＦ＝５ｃｍ、ＦＤ＝３ｃｍ

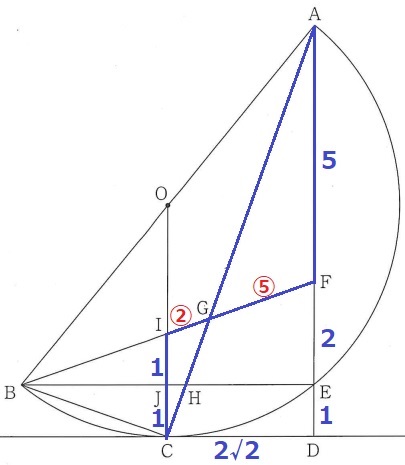
ＩＧを１辺とする三角形と相似になる三角形を探す。
→△ＩＧＣ∽△ＦＧＡ
ＪはＢＥの中点で△ＢＩＪ∽△ＢＦＥより、ＩＪ＝２÷２＝１ｃｍ
ＩＧ：ＧＦ＝ＩＣ：ＦＡ＝②：⑤

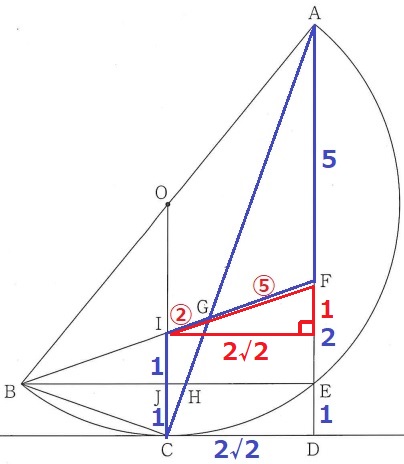
赤い直角三角形で三平方→ＩＦ＝３ｃｍ
したがって、ＩＧ＝３×②/⑦＝６/７ｃｍ