平均54.7点（前年比；＋10.6点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）ア 97.2％
－５－（－７）
＝－５＋７＝２
イ 90.2％
（１/４－２/３）×12
＝１/４×12－２/３×12 ←分配法則
＝３－８＝－５
ウ 83.0％
４ｘ×２/５ｘｙ÷２ｘ2
＝４/５ｙ
エ 73.4％
（－２ａ＋３）（２ａ＋３）＋９
＝－（２ａ－３）（２ａ＋３）＋９ ←マイナスを外にだすと和と差の積
＝－（４ａ2－９）＋９
＝－４ａ2＋９＋９
＝－４ａ2＋18
オ 80.4％
√24÷√８ｰ√12
＝√３－２√３
＝－√３
（２） 72.8％
100ａ＋50ｂ円を10で割る。
（100ａ＋50ｂ）/10＝ｃ ←左辺の分母を払う
100ａ＋50ｂ＝10ｃ
（10ａ＋５ｂ＝ｃ）
（３） 63.9％
150＝２×３×５2
（４） 75.1％
ｙ＝４（ｘ＋２） …①
６ｘ－ｙ＝－10 …②
①を展開した式を②に代入。
６ｘ－（４ｘ＋８）＝－10
２ｘ＝－２
ｘ＝－１
①に代入。
ｙ＝４×（－１＋２）＝４
ｘ＝－１、ｙ＝４
（５） 45.5％
反比例のグラフに関する正誤判定。
ア：双曲線。〇
イ：比例定数ａ＜０のとき、グラフは第二象限と第四象限にくる。
ｘ＜０のとき、グラフは第二象限でｙは正の値。ｘが増加するとｙも増加する。〇
ウ：反比例はｘとｙの積が比例定数ａで一定。〇
エ：反比例はｘ軸にもｙ軸にも接しない。あくまで近づくだけ！×
仮にｘ軸に交わるとして、ｙ＝ａ/ｘにｙ＝０をあてはめると、
０＝ａ/ｘ（ａ÷ｘ=０）となるが、０では割れない。
（６） 44.1％
無作為に取り出した34個のなかで、黒：白＝４：30＝２：15
最初に黒は100個入れたから、白の数は100×15/２＝750個
（７） 59.4％
28°を対頂角、35°を同位角でおろす。
△ＢＣＤで外角定理→∠ＡＣＢ＝ｘ＋35°
△ＡＢＣは二等辺だから、∠ＡＢＣ＝ｘ＋35°
28＋２（ｘ＋35）＝180
ｘ＝41°
（８） 34.4％
球の表面積Ｓ＝４πｒ2
半球の表面積は球の半分に円の面積を足せばいい。
４π×６2÷２＋６2×π＝108πｃｍ2
大問２（文字式・確率）
（１）
ルールに従って立式。
２×３＋７ｄ＋２×７＋３ｄ＝150
10ｄ＝130
ｄ＝13
３ｂ＋９ｃ＋３ｃ＋９ｂ
＝12（ｂ＋ｃ）＝168
ｂ＋ｃ＝14
ａ＝３、ｄ＝９、ａ＜ｂ＜ｃ＜ｄより、
ｂとｃは４以上８以下の範囲。
この範囲にある異なる２つの整数で和が14となる組合せを探す。
ｂ＝６、ｃ＝８
ア…13（76.1％）イ…12（60.3％）ウ…14（56.9％）
エ…６（34.1％）オ…８（36.2％）
（２）ア 59.2％
△ＡＯＱは直角二等辺三角形→∠ＰＡＱ＝45°
イ 20.2％！
ＰＱが直径、すなわち、ＰとＱが対極の位置にあれば、
円周角定理より、∠ＰＡＱ＝180÷２＝90°
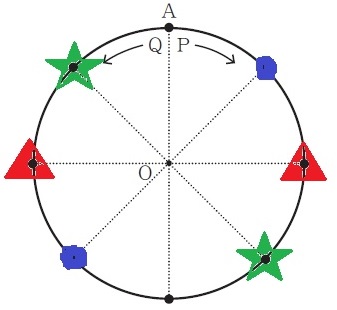
（Ｐ、Ｑ）の組み合わせ。
●…（１、３）
▲…（２、２）（６、６）
★…（３、１）
以上、４通り。
４/36＝１/９
大問３（図形）
（１）立体図形
ア 75.2％
三角形ＢＣＨの内角は45°－45°－90°で直角二等辺三角形。
ＢＨ＝６ｃｍ
直角三角形ＡＢＨの３辺の比は３：４：５
ＡＨ＝８ｃｍ
イ 44.2％
上下に２つの円錐がくっついた形になる。
高さはＡＣ＝14ｃｍで一括処理。
６×６×π×14÷３＝168πｃｍ3
ウ 40.1％
円錐の側面積となる扇形の中心角を求める。
〔扇形の中心角…360°×半径/母線〕
よって、360×６/10＝216°
（２）平面図形
ア
△ＡＢＥ∽△ＣＢＤの照明。
複雑な図形ではないが、丁寧な誘導がついている。
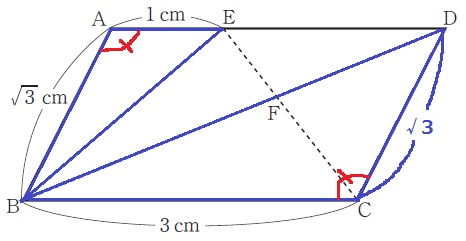
平行四辺形の対角は等しい。
∠ＢＡＥ＝∠ＢＣＤ
辺の比に着目する。
ＡＥ：ＣＤ＝１：√３
ＡＢ：ＣＢ＝√３：３＝１：√３（√３で割る）
よって、ＡＥ：ＣＤ＝ＡＢ：ＣＢ
したがって、２辺の比とあいだの角が等しいから∽。
あ…∠ＢＣＤ（83.0％）い…√３（77.9％）
う…ＣＢ（88.4％）え…比（78.0％）
イ 5.3％!!
△ＢＣＦ∽△ＤＥＦより、ＢＦ：ＤＦ＝３：２
△ＢＣＦの面積を【３】とおくと、△ＤＣＦの面積は【２】
△ＢＣＤの面積は【５】で、これは平行四辺形ＡＢＣＤの半分にあたる。
△ＡＢＤの面積も【５】となる。
ＡＥ：ＥＤ＝１：２より、△ＡＢＥ＝【５】×１/３＝【５/３】
△ＢＣＦ：△ＡＢＥ＝【３】：【５/３】＝９：５
よって、９/５倍
大問４（関数）
（１） 65.2％
原点の通過に注意！
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、最大値ｙ＝３
０≦ｙ≦３
（２） 55.9％
ｙ＝－１/２ｘ2に代入。
Ａ（－４、－８）⇒Ｂ（２、－２）
右に６、上に６で傾きは６/６＝１
Ａから右に４、上に４で切片は－４。
ｙ＝ｘ－４
（３）ア 49.4％
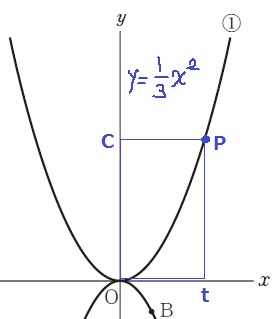
Ｐのｘ座標をｔとおく。
ｙ＝１/３ｔ2
イ 25.7％！
ＯＣ＋ＣＰ
＝１/３ｔ2＋ｔ＝18
１/３ｔ2＋ｔ－18＝０ ←全ての項を３倍
ｔ2＋３ｔ－54
＝（ｔ＋９）（ｔ－６）＝０
ｔ＞０より、ｔ＝６（Ｐのｘ座標）
ｙ＝１/３ｘ2に代入→Ｐ（６、12）
大問５（数量変化）
（１） 63.4％
図４に注目。
４～8分後の底面Ａの水面が12ｃｍのままなのは、
水が仕切り①を超えて底面Ｂに移動したから。
よって、仕切り①の高さａは12ｃｍ。
（２）
底面Ａでは４分後に12ｃｍなので、
水面は１分あたり12÷４＝３ｃｍずつ上昇する。
１分後の水面は３ｃｍ（あ…３） 67.9％
図２より、底面Ｂの面積は底面Ａと同じ。
つまり、水面の上昇速度も同じＡと同じ！
水を入れてから５分後は、Ｂに水が入ってから１分後。
つまり、Ｂの水面は３ｃｍ（い…３） 49.8％
８分後以降は底面積が〔底面Ａ＋底面Ｂ〕と２倍に増える。
底面積が２倍→水面の上昇速度が１/２倍
つまり、８分以降は仕切り②まで１分あたり1.5ｃｍずつとなる。
８分＋（18－12）ｃｍ÷1.5＝12分（う…12） 28.3％！
＠別解＠
↑横から見た図。
12ｃｍまで８分かかるので、
18ｃｍは、８分×18/12＝12分
（３） 24.4％！
底面Ｂが基準になる。
０～４分までは０ｃｍ。
４分後から水が入り、８分後に12ｃｍ。
８分後は１分あたり1.5ｃｍ上昇。
21ｃｍに達するまでの時間を求める。
８分＋（21－12）÷1.5＝14分
ちょうど14分後に仕切り②と同じ21ｃｍになる。
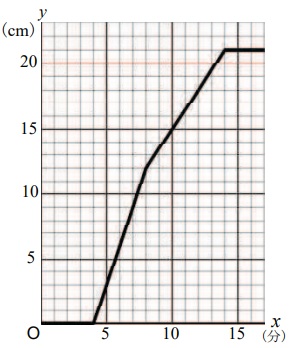
（４、０）から（８、12）、そこから（14、21）まで直線でひく。
（４） 18.2％！
14分後、Ｃに注水。
底面ＣはＡとＢと同じ面積→Ｃの水面上昇速度は１分３ｃｍ。
残り６分で水面は18ｃｍ。これは仕切り②より低い。
よって、18ｃｍ。
以下、公式の講評を参考に書いています。
大問１
（３）素因数分解が64％。ここで失点したくはない。
（４）ｙ＝（ｘ＋２）の展開を間違えて代入した誤答が多かった。
（５）最も判別しにくいイを選んだ誤答が多かった。
（８）円の部分を加えない72πや半球の体積を求めた144πが多かった。
大問２
（１）失点の原因は条件の理解不足。
大問３
（１）ウ公式では『おうぎ形の展開図から中心角を求める方程式をつくることができなかった』
と方程式を想定していたようだが、360°×半径/母線で瞬殺できることも知っておこう。
（２）イ図形のラストはだいたいどこも難しい問題を出してくるが、
今回は比較的やりやすかったと思うのに正答率は５％であった。
大問５
ここも基本～標準。
（３）アＰのｘ座標をｔと置いたときのｙ座標。
ｙ＝１/３ｘ2のｘをｔに置き換えて終わりだが、正答率は半分を下回った。
大問６
本問も条件読解が鍵となる。
横から見た図で整理するとわかりやすい。どの順でどの空間が埋まっていくか。
どのくらいの速さで水が埋まっていくかを見極める。
基本～標準で占めているので、得点分布が良い感じで分散している。
ただ、もう少し解けても良さそうな設問がちょこちょこあったので、
ワークにある典型問題はきちんと解法をおさえておこう。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント