2022年度　埼玉県公立高校入試問題過去問【数学】解説

平均48.0点（前年比；－14.2点）

問題はコチラ→ＰＤＦファイル
2022年度・埼玉数学（学校選択）の解説はコチラ。

大問１（小問集合）

（１）　96.7％
７ｘ－９ｘ
＝－２ｘ

（２）　81.8％
５×（－３）－（－２）
＝－15＋２
＝－13

（３）　80.9％
12ｘ²ｙ÷３ｘ×２ｙ
＝８ｘｙ²

（４）　76.2％
７ｘ－２＝ｘ＋１
６ｘ＝３
ｘ＝１/２

（５）　81.5％
12/√６－３√６
＝２√６－３√６
＝－√６

（６）　84.5％
ｘ²－ｘ－20
＝（ｘ＋４）（ｘ－５）

（７）　82.2％
４ｘ－３ｙ＝10　…①
３ｘ＋２ｙ＝－１　…②
①×２＋②×３をすると、17ｘ＝17
ｘ＝１
②に代入して、３＋２ｙ＝－１
ｙ＝－２
ｘ＝１、ｙ＝－２

（８）　70.6％
２ｘ²－３ｘ－３＝０
解の公式を適用して、ｘ＝（３±√33）/４

（９）　60.4％

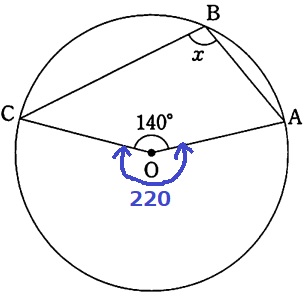
中心角は、360－140＝220°
ｘ＝220÷２＝110°

（10）　50.5％

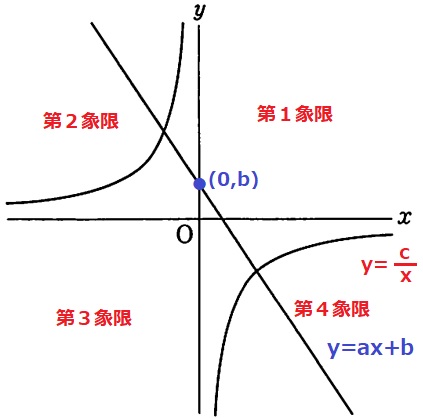
ｙ＝ａｘ＋ｂは右下の直線だから傾きａ＜０
切片ｂはｘ軸より上にあるのでｂ＞０
反比例は比例定数が正だと第１象限と第３象限に、
負だと第２象限と第４象限に双曲線が描かれる。ｃ＜０
カ

（11）　36.6％
側面積の中心角は〔×半径/母線〕で対処。
360×３/８＝135°

（12）　14.2％！

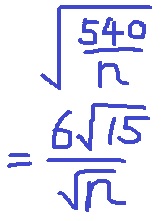
↑これが自然数になるようなｎは、15×（６の約数の平方数）
６の約数は〔１・２・３・６〕なので、ｎは４通り。
*具体的な数値でいえば、ｎ＝15×１^２＝15、15×２^２＝60、
15×３^２＝135、15×６^２＝540の４つ。

（13）　21.1％！

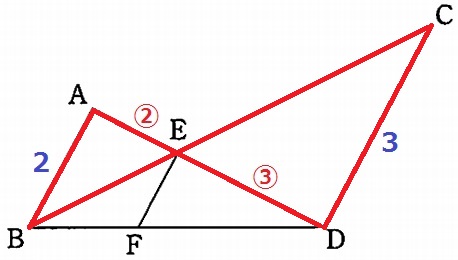
△ＡＢＥ∽△ＤＣＥより、ＡＥ：ＥＤ＝②：③

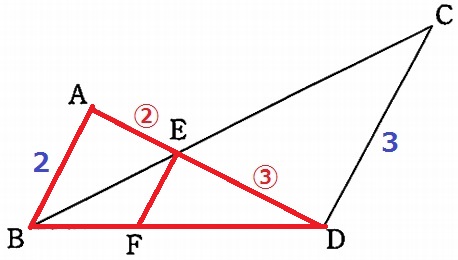
△ＡＢＤ∽△ＥＦＤで、ＥＦ＝２×③/⑤＝６/５ｃｍ

＠余談＠

受験業界では「和分の積」とよばれる形で、ＥＦ＝（２×３）/（２+３）＝６/５
ＡＢ＝３、ＣＤ＝７であれば、ＥＦ＝（３×７）/（３+７）＝21/10になる。

（14）　53.1％
高校から降りてきた箱ひげ図。

ｱｲ：四分位範囲は、上位グループの真ん中である第３四分位数（Q3）から、
下位グループの真ん中である第１四分位数（Q1）をひいた値。
極端な外れ値を除外するので、その影響を受けにくい。〇
ウ：平均は×印などで示す。箱の中央にあるとは限らない。×
エ：第２四分位数は中央値。〇
ウ

（15）　40.9％
印アリが③、印ナシが⑳、全体が㉓。
22匹が③に相当するので、総数は22×㉓/③＝506/３＝168.6…≒169匹

（16）　4.0％!!

さすが公式解答、手際が良い(;`ω´)
体積比は相似比の３乗。
ＳとＭの体積比と価格の比から、ＳよりＭが割安とわかる。
Ｍ：Ｌは半径の相似比４：５→底面積の比16：25→体積比16：50
価格の比に照らしてＭよりＬが割安だから、最も割安なのはＬサイズ。

連比で体積比を統一させることもできる。
１円あたりの体積比（27÷160…64÷320…200÷960）は計算が大変なので、
値段の比がＳ：Ｍ：Ｌ＝１：２：６と整っている点に気がつきたい。

大問２（作図・関数）

（１）　36.6％

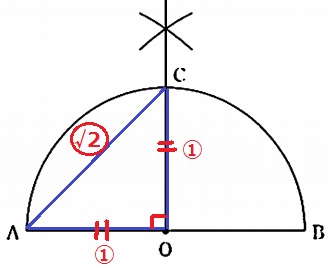
１：√２とくれば、直角二等辺三角形の辺の比。
ＡＣを斜辺とする直角二等辺を作図するには、
Ｏを通るＡＢの垂線をひけばいい。弧ＡＢとの交点がＣ。

（２）　21.8％！

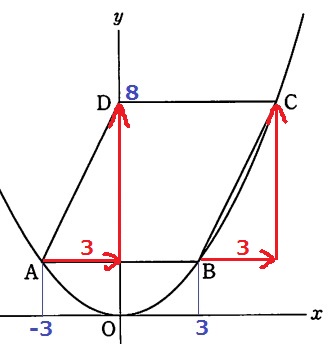
ＡからＤまでの動きと、ＢからＣまでの動きは同じ。
Ｃのｘ座標は３＋３＝６
ｙ座標はＤと同じ８→Ｃ（６、８）
これをｙ＝ａｘ²に代入すると、
８＝36ａ
ａ＝２/９

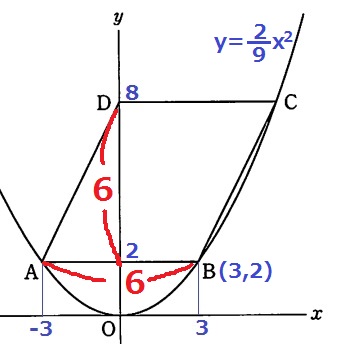
ｙ＝２/９ｘ²にｘ＝３を代入。Ｂ（３、２）
平行四辺形の底辺が６。高さは８－２＝６だから６×６＝36ｃｍ²
ａ＝２/９、36ｃｍ²

大問３（確率）

（１）　49.2％
右に１、上に２だから傾きは２。
ｙ軸方向に直線を延長すると切片は－３。
ｙ＝２ｘ－３

（２）　31.4％！

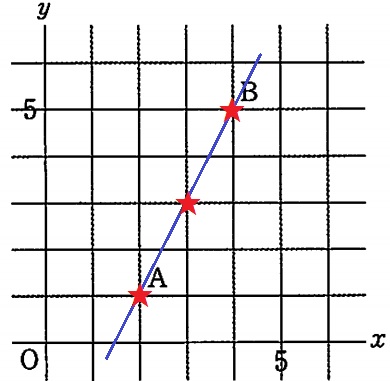
（２、１）（３、３）（４、５）だと直線ＡＢとかぶり、三角形ができない→３個
全体は６×６＝36通りだから、三角形ができるのは36－３＝33通り
ア…３、イ…33

（３）　0.7％!!!
やや難レベルのうえに説明要求付き(´Д`; )

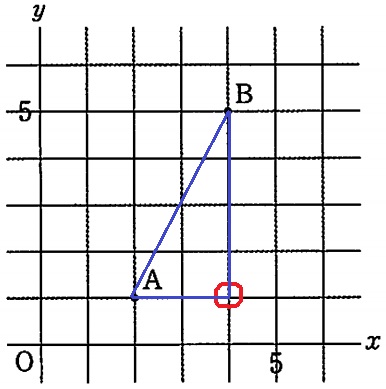
明らかに４ｃｍ²とわかる三角形から考える。
（４、１）の点に注目する。

これを通る傾き２の平行線をひく。
このライン上にＰがくると、等積変形で△ＡＢＰの面積はちょうど４ｃｍ²だから、
このラインを含む右側の点（ｘ、ｙ≦６）すべてが該当する。

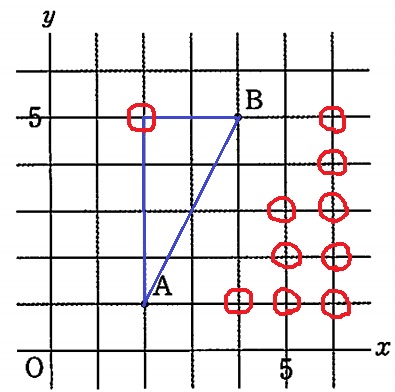
反対側で同じことをする。（２、５）に注目。

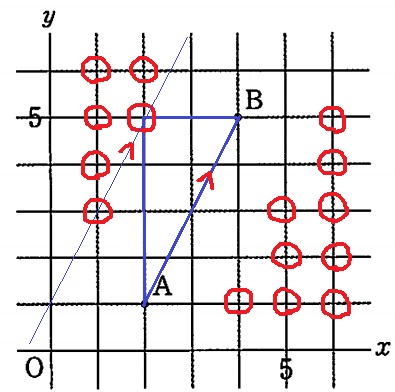
傾き２のラインを含む左側すべての点が該当。
４ｃｍ²以上となるのは15通り、全体が33通りだから、
確率は15/33＝５/11

大問４（平面図形）

（１）　13.2％！
ＰＡ＝ＰＢの証明。
円外の点Ｐからの接線の長さが等しいことを証明する。

△ＡＰＯと△ＢＰＯに注目する。
ＰＯは共通辺、半径よりＯＡ＝ＯＢ
半径と接線は垂直に交わるので、∠ＰＡＯ＝∠ＰＢＯ＝90°
斜辺と他の１辺が等しい直角三角形ゆえ△ＡＰＯ≡△ＢＰＯ
対応する辺は等しいから、ＰＡ＝ＰＢ

（２）　0.3％!!!

半径を作図し、Ｐ・Ｒ・Ｑを結ぶ。
ＲＯ＝ＲＱ＋ＱＯ＝３＋５＝８ｃｍ

円Ｒと直線ℓの接点をＤとする。
△ＰＲＤ∽△ＰＯＡで、相似比はＲＤ：ＯＡ＝３：５
ＰＲ＝８×３/２＝12ｃｍ

ＰＤ：ＤＡ＝③：②
点Ｃをどうするか。。

内接円の問題で見たことがあると思う。
★ペアと＠ペアの三角形は（１）の証明と同様の理由で合同。
ＤＣ＝ＱＣ＝ＡＣ
ＤＣ＝②÷２＝①

△ＰＲＤで三平方→ＰＤ＝３√15ｃｍ
ＰＣ＝３√15×④/③＝４√15ｃｍ