2019年度　三重県公立高校過去問後期【数学】解説

平均26.5点（50点満点）
問題はコチラ→ＰＤＦファイル
前期解説はコチラ。

大問１（計算）

（１）
（－20）÷４
＝－５

（２）
ｘ/２－ｘ/３
＝（３ｘ－２ｘ）/６
＝１/６ｘ

（３）
３（ａ＋２ｂ）－（２ａ－ｂ）
＝３ａ＋６ｂ－２ａ＋ｂ
＝ａ＋７ｂ

（４）
（√７－２√５）（√７＋２√５）　←和と差の平方の形になる！
＝√７²－（２√５）²
＝７－20＝－13

（５）
ｘ²－ｘ－30
＝（ｘ－６）（ｘ＋５）

（６）
２ｘ²－３ｘ－１＝０
因数分解ができないので、解の公式を適用。
ｘ＝（３±√17）/４

（７）
取り出す白玉をｘ個とすると、取り出す赤玉は２ｘ個。
45－２ｘ：27－ｘ＝７：５
７（27－ｘ）＝５（45－２ｘ）
12個

大問２（小問集合）

（１）①
Ｂを仮の平均とする。
（＋10＋０＋２－３＋４－１）÷６＝＋２
Ｂは読書目標の６冊なので、６人の平均値は６＋２＝８冊

②
６人の中央値（メジアン）→３番目と４番目の平均。
３番目…Ｂ６冊
４番目…Ｃ８冊
（６＋８）÷２＝７冊

（２）
連立方程式。誘導の空欄を埋める。
定価10％引き→定価の90％（９割）
定価20％引き→定価の80％（８割）
これさえ踏まえれば立式ができるはず。
①…ｘ＋ｙ
②90/100（0.9）ｘ×２＋80/100（0.8）ｙ×３
③…90、④…55

（３）①
【少なくとも１枚裏＝全体－全部表】
全体…２⁴＝16通り
全部表…１通り
１－１/16＝15/16

②
表が510円以上ということは、500円玉は絶対に表。
残る10円、50円、100円で10円以上となれば良い。
すなわち、３枚のうち、少なくとも１枚が表になれば良い。
【少なくとも１枚表＝全体－全部裏】
２³－１＝７通り
７/16

大問３（関数）

（１）
ｙ＝－ｘ＋６に代入。
Ａ（３、３）
ｙ＝ａｘ²に代入。
３＝９ａ
ａ＝１/３

同様に、ｙ＝－ｘ＋６に代入。
ｐ＝－（－６）＋６＝12

（２）
ｘ＝０のとき、最小値ｙ＝０
ｘ＝４のとき、最大値ｙ＝16/３
０≦ｙ≦16/３

（３）
ＥＦ＝－ｘ＋６－１/３ｘ²
ＦＧ＝１/３ｘ²

ＥＦ＝２ＦＧ
－ｘ＋６－１/３ｘ²＝１/３ｘ²×２
－３ｘ＋18－ｘ²＝２ｘ²
３ｘ²＋３ｘ－18
＝（ｘ＋３）（ｘ－２）＝０
ｘ＜０より、ｘ＝－３

（４）
Ｃのｘ座標は正。
△ＡＢＣと△ＯＡＢは辺ＡＢが共通している。
Ｏはすでにｘ軸上にいるので、等積変形で動かせない。
そこで、△ＡＢＣ以外で△ＯＡＢと面積が等しくなる三角形を考える。

ＯＡの傾きは１、ＢＡの傾きは－１。
ここからＯＡとＢＡは垂直に交わる。（直線が垂直に交わると傾きの積は－１）

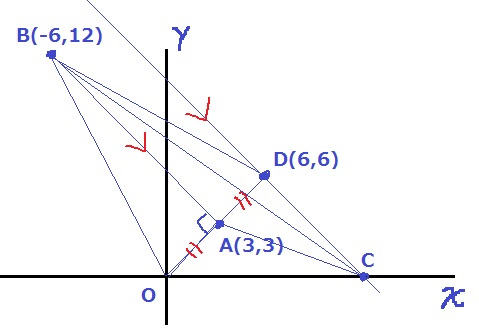
ＯＡを延長し、ＯＡと同じ距離にある点をＤとする。
Ｄ（６、６）
△ＯＡＢと△ＤＡＢは合同で面積が等しい。
ここで、Ｄを等積変形でｘ軸方向に移動させる。
ＡＢの傾きは－１なので、ＣＤの傾きも－１。
Ｄ（６、６）だから、
６＝６×（－１）＋ｂ
ｂ＝12
ＣＤ：ｙ＝－ｘ＋12
ｙ＝０のとき、ｘ＝12
Ｃ（12、０）

大問４（作図・空間図形）

（１）
四角形の内部に菱形を作図する。
菱形は４辺の長さが等しいので、ＰやＱに目が行きがちになるが、
先にＲを作っておくことがポイント！

菱形の対角線ＢＲは∠ＰＢＱを二等分する。
ＰはＢＡ上のどこか、ＱはＢＣ上のどこかにあるので、
①∠ＡＢＣの二等分線を作図する。
Ｒの位置が決まったら、菱形の対角線は各々の中点で垂直に交わるので、
②ＢＲの垂直二等分線を描く。
この線分とＡＢとの交点がＰ、ＢＣとの交点がＱとなる。

（２）①
円錐の高さは三平方→√（６²－３²）＝３√３ｃｍ
３×３×π×３√３×１/３＝９√３πｃｍ³

②
側面の扇形の中心角…360×半径/母線
端的にいえば、側面の扇形の面積＝円の面積×半径/母線
６×６×π×３/６＝18πｃｍ²
*求めるのは側面積なので、底面積は不要！
半径/母線＝３/６なので、側面の扇形は半円となる。

③
ＡＢは底面の直径。
孤ＡＢでいえば、底面の円周の半分にあたる。
底面の円周は側面の扇形（半円）の孤の長さに等しいので、
孤ＡＢはその半円の半分にあたる。

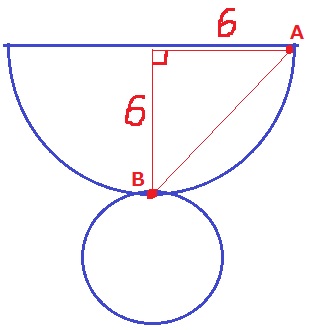
ひもの長さは直線ＡＢ。
１：１：√２の直角三角形から、ひもの長さは６√２ｃｍ。

大問５（平面図形）

（１）
△ＤＢＣ∽△ＤＥＧの証明。

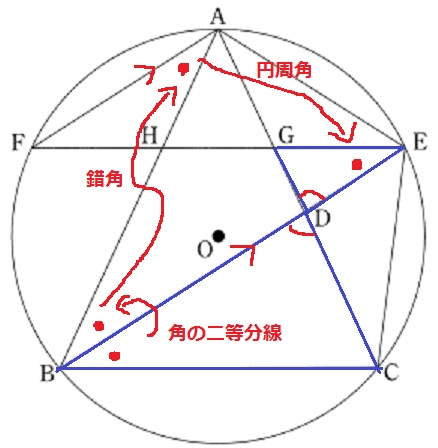
誘導があるのでありがたし。
対頂角＋①角の二等分線②錯角③孤ＢＦに対する円周角。
以上の流れから２角が等しい点を指摘する。
ア…∠ＥＤＧ、イ…∠ＤＢＡ、ウ…２組の角
*角度は対応する順に書けるようにしておこう。

（２）
△ＡＥＧ≡△ＡＦＨの証明。
誘導がなく、手順が多い。

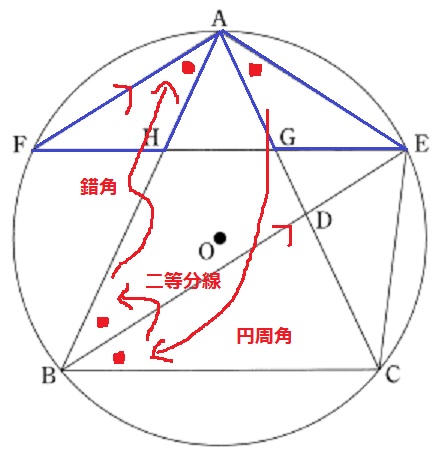
∠ＥＡＧから出発して、①孤ＣＥに対する円周角②角の二等分線③錯角
これで１つの角が共通する。

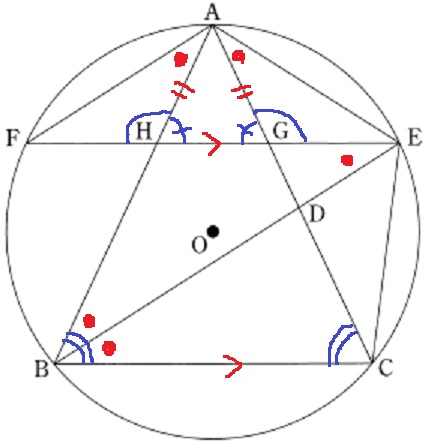
前問の相似から、∠ＤＢＣ＝∠ＤＥＧ
錯角が等しく、ＢＣ//ＦＥ
これを利用して、△ＡＨＧ∽△ＡＢＣ（２角）となり、
ＡＧ：ＡＣ＝ＡＨ：ＡＢ
△ＡＢＣは二等辺なので、ＡＢ＝ＡＣと組み合わせてＡＧ＝ＡＨ
△ＡＨＧは二等辺で底角が等しい。∠ＡＧＨ＝∠ＡＨＧ
反対側の角度も等しくなるので、∠ＡＧＥ＝∠ＡＨＦ
一辺両端角が等しく合同となる。

＠別解＠

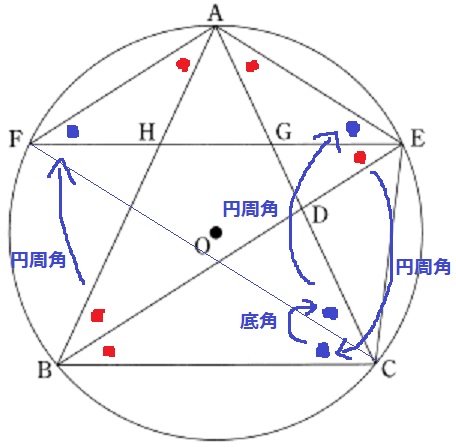
●は先ほど指摘した通り。
ここから●も等しい角度であることを証明する。
まず、弧ＡＥに対する円周角から、∠ＥＢＡ＝∠ＥＦＡ
弧ＢＦに対する円周角より、∠ＦＥＢ＝∠ＦＣＢ
△ＡＢＣ（二等辺）の底角に注目し、●＋●＝∠ＡＣＦ＋●だから、
∠ＡＣＦ＝●
弧ＡＦに対する円周角より、∠ＡＣＦ＝∠ＡＥＦ

△ＡＥＦは二等辺なので、ＡＥ＝ＡＦ
もしくは、∠ＡＢＥ＝∠ＡＣＦと円周角が等しいことから、弦が等しいとしても良い。
こうして一辺両端角が導ける。

（３）①
しょっぱなから迷う(;`ω´)
ＡＢとＢＣしか長さが判明していない。

Ａを通り、ＢＣに平行な線をひき、ＢＥとの交点をＪとおく。
ＡＪ//ＢＣより、錯角で∠ＪＢＣ＝∠ＢＪＡ
△ＡＢＪは二等辺三角形となり、ＡＪ＝３ｃｍ
△ＡＤＪ∽△ＣＤＢより、ＡＤ：ＤＣ＝ＡＪ：ＣＢ＝３：２

ＡＣ＝３ｃｍなので、
ＤＣ＝３×２/５＝６/５ｃｍ

＠別解＠
この問題を見たときに、真っ先に思いついたのは角の二等分線の定理でした。

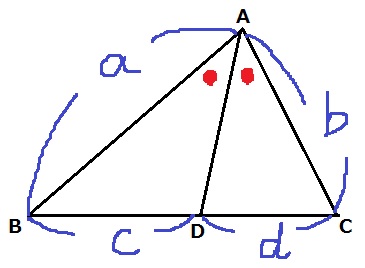
角ＢＡＣの二等分線があったとき、ａ：ｂ＝ｃ：ｄが成り立つ。
高校数学で習いますが、中学の相似で証明できるので覚えておいた方が良いかも。

Ｃを通る、ＢＤに平行な線をひいて、ＡＢの延長との交点をＩとおく。
平行線から等しい錯角と同位角を調べると、△ＢＩＣが二等辺。
ＢＩ＝ＢＣ＝２ｃｍ
△ＡＢＤ∽△ＡＩＣから、ＡＢ：ＢＩ＝ＡＤ：ＤＣ＝３：２
ＤＣ＝３×２/５＝６/５ｃｍ
*本問は角の二等分線の定理を使えるかで、ほぼ決着がつきそうな感じがします。
ここを落とすと②③も自動的に落とすので、問題の構造が意地悪な気もする…。

②
等角が多い図形なので、
円周角や錯角、合同で示せた等しい角に印をつけておく。
すると、△ＡＧＥは二等辺三角形とわかる。

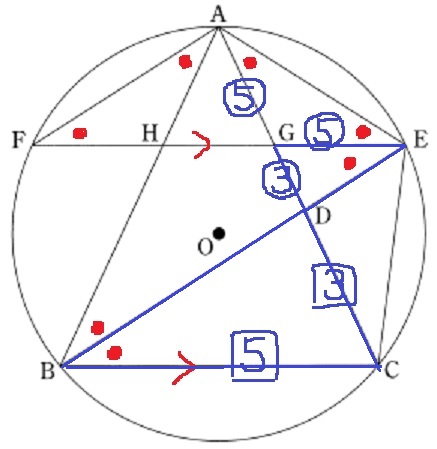
（１）で証明した△ＤＢＣ∽△ＤＥＧを用いる。
ＧＥ：ＧＤ＝ＣＢ：ＣＤ＝２：６/５＝⑤：③
ＡＧ＝ＧＥから、ＡＧ＝⑤
ＡＤ＝ＡＣ－ＤＣ＝３－６/５＝９/５ｃｍ
ＧＤ＝９/５×３/８＝27/40ｃｍ

③
ＣＤ：ＤＧ＝６/５：27/40＝16：９
△ＤＢＣ∽△ＤＥＧで、面積比は辺の２乗だから、
△ＤＢＣ：△ＤＥＧ＝16²：９²＝256：81

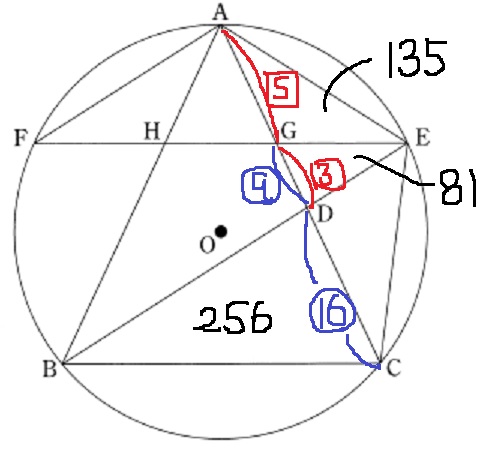
△ＡＦＨは（２）から△ＡＥＧと合同。
前問より、ＡＧ：ＧＤ＝５：３なので、
△ＡＥＧ＝81×５/３＝135
したがって、△ＡＦＨ：△ＤＢＣ＝135：256
公立高校入試解説ページに戻る