2023年度　鹿児島県公立高校入試問題過去問【数学】解説

平均47.0点（前年比；＋8.0点）

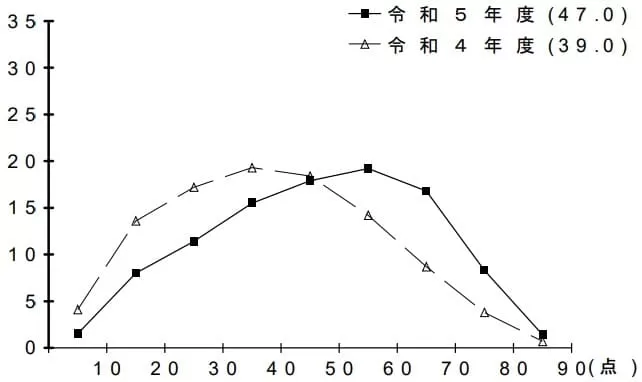
０～10点…1.5％、11～20点…8.0％、21～30点…11.4％、31～40点…15.5％
41～50点…17.9％、51～60点…19.2％、61～70点…16.8％、71～80点…8.3％、81～90点…1.4％
問題はコチラ→ＰＤＦファイル

大問１（小問集合）―71.0％

（１）①　97.5％
63÷９－２
＝７－２
＝５

②　92.1％
（１/２－１/５）×１/３
＝３/10×１/３
＝１/10

③　76.1％
（ｘ＋ｙ）²－ｘ（ｘ＋２ｙ）
＝ｘ²＋２ｘｙ＋ｙ²－ｘ²－２ｘｙ
＝ｙ²

④　58.2％
絶対値…数直線上で原点０からの距離。
７より小さいだから、７は含まない。
０、±１、±２、±３、±４、±５、±６の13個。

⑤　62.1％
√ａの形にして比較する。
３√２＝√18
２√３＝√12
４＝√16
３√２＞４＞２√３
ア

（２）　84.9％
３ｘ＋ｙ＝８　…①
ｘ－２ｙ＝５　…②
①×２＋②
７ｘ＝21
ｘ＝３
①に代入、３×３＋ｙ＝８
ｙ＝－１
ｘ＝３、ｙ＝－１

（３）　54.2％
（10、10）（10、50）（10、100）（50、100）の４通り。

（４）　75.4％
９÷11＝0.818181…
小数第20位は偶数番目だから１。

（５）　38.6％
それぞれの中学校の200～220ｃｍの人数を求める。
Ａ中学校…20人×35/100＝７人
Ｂ中学校…25人×44/100＝11人
生徒の合計は45人だから、相対度数は18/45＝２/５＝0.40

大問２（小問集合２）―50.3％

（１）①　79.7％
Ｎ角形の内角の和は、180（Ｎ－２）°
180×（５－２）＝540°

②　21.8％！
ア：４つの角が等しい→長方形
イ：４つの辺が等しい→菱形
ウ：２組の対辺がそれぞれ平行→平行四辺形
エ：対角線が垂直に交わる→菱形の”性質”
イ

＠図形の性質＠
●平行四辺形
【定義】
２組の対辺がそれぞれ平行である四角形。
【性質】
①２組の対辺は等しい。
②２組の対角も等しい。
③対角線はおのおのの中点で交わる。

以下の図形は、平行四辺形の性質を兼ね備える。
●長方形
【定義】４つの角が等しい四角形。
【性質】対角線の長さが等しい。
●菱形
【定義】４つの辺が等しい四角形。
【性質】対角線が垂直に交わる。
●正方形
【定義】４つの角と４つの辺が等しい四角形。
【性質】対角線の長さが等しく、垂直に交わる。

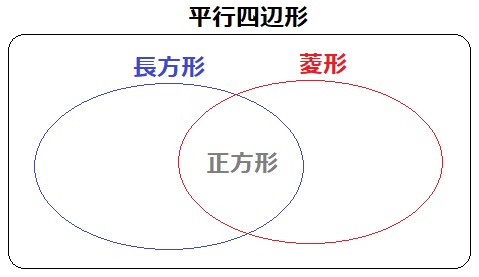
ベン図で関係性をあらわすと、このようになる。
長方形や菱形は特別な平行四辺形、正方形は特別な長方形・菱形。

③　67.2％
いろいろな出し方がある。以下は一例。

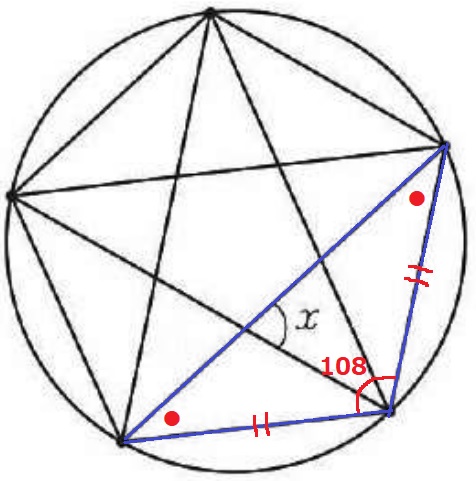
青線の三角形は正五角形の１辺を等辺とする二等辺三角形。
底角を●とする。

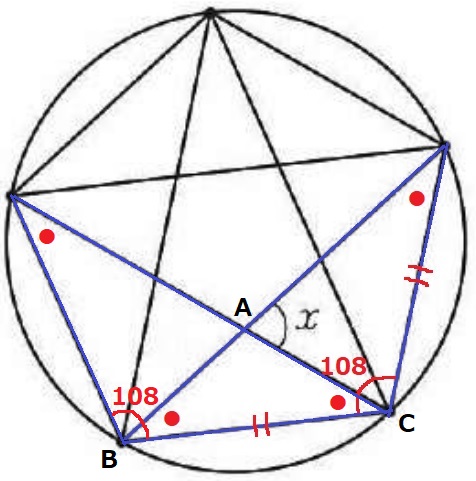
左側にも合同の二等辺がある。
△ＡＢＣで外角定理→ｘ＝●●
二等辺の内角より、ｘ（●●）＝180－108＝72°

（２）　49.7％
ＢＥ＝ＣＥ→ＥはＢとＣから等距離にある→ＢＣの垂直二等分線上。
問題は、『△ＢＣＥと長方形ＡＢＣＤの面積は等しい』をどう扱うか。

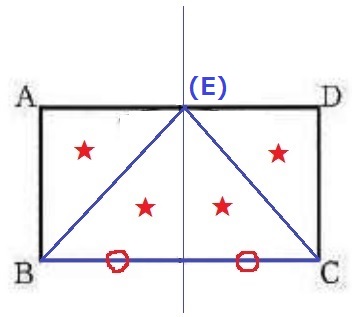
仮にＥがＡＤ上にあった場合、上図のように分割すると、
△ＥＢＣの面積は長方形ＡＢＣＤの半分である。

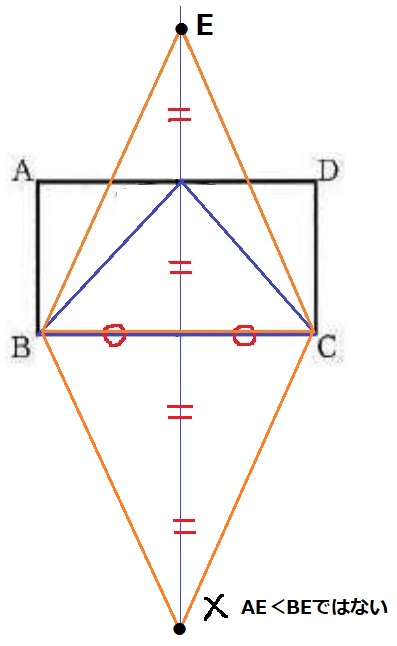
高さを２倍すれば面積が２倍になり、長方形ＡＢＣＤと等積になる。
辺ＢＣの反対側にも等積の三角形を作れるが、ＡＥ＜ＢＥの条件に反してしまう。

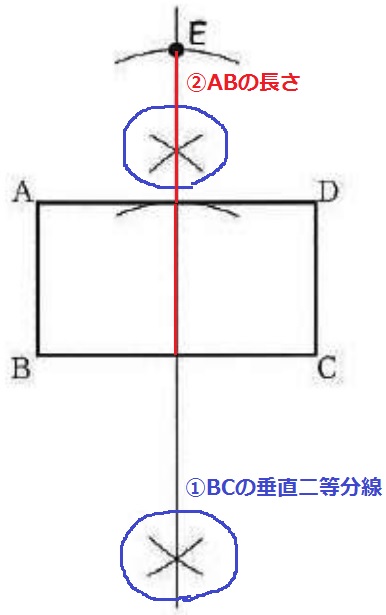
①ＢＣの垂直二等分線。
②ＢＡの長さをとり、辺ＡＤ上の交点から上に向かって長さを移す。
交点がＥ。

（３）　37.8％
答案では方程式とともに計算過程も書く。
底面積はｘｃｍ²の正方形。側面積の１面は３ｘｃｍ²の長方形。
ｘ²×２＋３ｘ×４＝80
２ｘ²＋12ｘ－80＝０　←÷２
ｘ²＋６ｘ－40
＝（ｘ＋10）（ｘ－４）＝０
ｘ＞０より、ｘ＝４
４ｃｍ

大問３（データの活用）―63.0％

（１）　67.4％
数学では特殊な問題。
1950年から55年は増加して最大になる。この時点でア・イが外れる。
その後は減少が多いが、80年と85年は増加に転じている。
エ

（２）①　62.6％
鹿児島は13～14％の階級に含まれる。
階級値は13と14の平均で13.5％

②　29.1％
最小値は９～10％、最大値は16～17％でいずれも同じ。
47都道府県の第２四分位数（中央値）は24番目の値→12～13％の階級
第１四分位数は下位23個の真ん中、下から12番目→11～12％の階級
第３四分位数は上位23個の真ん中、上から12番目→12～13％の階級
第１四分位数と第３四分位数が合っているのはイしかない。
第２四分位数の12％は12％以上13％未満の階級に含まれる。
イ

（３）①96.5％、②85.9％、③51.3％、④46.9％、⑤64.2％
①範囲＝最大値－最小値。図２で最も範囲が小さいのは2000年。×
②図３で1980年の第３四分位数は15％を超えている。〇
③図２の2010年と2020年はともに第３四分位数が15％弱。
上から11番目の値は同程度だが、データの詳細はわからない。△
④図３の2000年は第１四分位数が25％超⇒上から33番目が25％超。〇
⑤平均値を×印などで示す箱ひげ図もあるが、図２にはないので不明。△
①…イ、②…ア、③…ウ、④…ア、⑤…ウ

大問４（関数）―38.7％

（１）　83.0％
ｙ＝１/４ｘ²にｘ＝４を代入して、ｙ＝４

（２）　33.2％！

Ｂのｘ座標を小さくする⇒Ｂを左側（Ｂ’）に移す。
ア：ＡＢの傾きは緩やかで小さくなる。〇
イ：切片は大きくなる。×
ウ：Ｃは左側（Ｃ’）に移動する⇒Ｃのｘ座標は小さくなる。〇
エ：辺ＯＡは固定。Ｃ’はＣよりＯＡから離れるので、△ＯＡＣの面積は大きくなる。×
ア・ウ

（３）①　41.9％
答案では求め方や計算過程も記述する。
ｙ＝１/４ｘ²にｘ＝－２を代入すると、Ｃのｙ座標は１。
Ｃ（－２、１）→Ａ（４、４）
右に６、上に３だから、傾きは３/６＝１/２
Ｃから左に２、下に１移動してｘ軸に着く。
Ｂのｘ座標は－２－２＝－４
Ｂ（－４、０）

記述の仕方は公式解答を参照。
もう少し簡略して書いても大丈夫だと思う。

②　5.6％!!
ここで確率の問題が登場した。

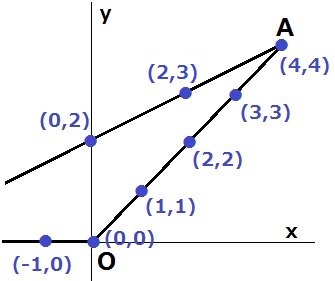
先にａ－２とｂ－１の範囲を確定しておく。
１≦ａ、ｂ≦６
－１≦ａー２≦４、０≦ｂ－１≦５
ＡＯの傾きは１．ＡＢの傾きは１/２。
ｘ座標が－１～４、ｙ座標が０～５である、辺上の格子点を調べると上図の８個が該当する。
出目は全部で６×６＝36通りだから、確率は８/36＝２/９

大問５（平面図形）―22.5％

（１）　70.2％
△ＡＢＣで三平方→ＡＣ＝３√５ｃｍ

（２）　18.2％！
△ＡＣＦが二等辺三角形である証明。

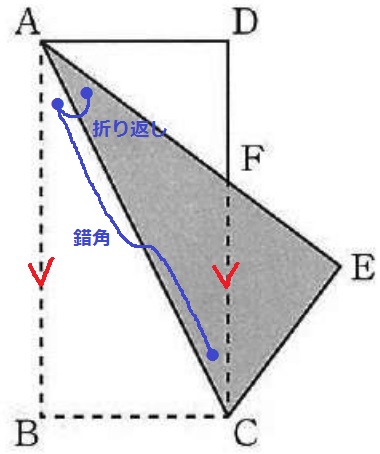
折り返し＋ＡＢ//ＤＣの錯角から底角が等しいので、△ＡＣＦは二等辺三角形。

（３）　10.1％！

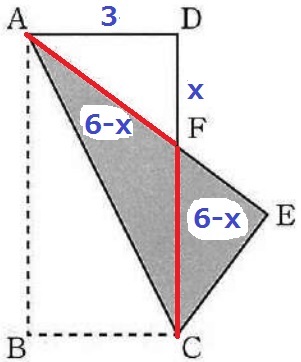
ＤＦ＝ｘｃｍとすると、ＦＣ＝６－ｘｃｍ
△ＡＣＦは二等辺だから、ＡＦ＝６－ｘｃｍ
△ＡＦＤで三平方。
（６－ｘ）²＝ｘ²＋９
36－12ｘ＋ｘ²＝ｘ²＋９
ｘ＝９/４
ＤＦ＝９/４ｃｍ

（４）　1.3％!!

左右に同じように折り返すので、△ＡＨＪと△ＤＦＪは対称性から合同。
ＡＨ＝ＤＦ＝９/４ｃｍ
四角形ＡＨＦＤは長方形で対角線は各々の中点で交わる→ＪはＨＤの中点。
△ＡＨＤの半分が△ＡＨＪにあたる。ＨＩ：ＩＪの比が知りたい。

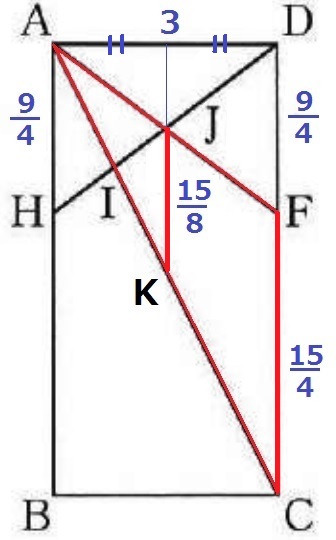
比の合成で良いのですが…少し手法を変えてみます。
ＦＣ＝６－９/４＝15/４ｃｍ
Ｊから真下に線をひき、ＡＣとの交点をＫとする。
ＪとＫはそれぞれＡＦとＡＣの中点で、△ＡＫＪ∽△ＡＣＦの相似比は１：２。
ＪＫ＝15/４÷２＝15/８ｃｍ

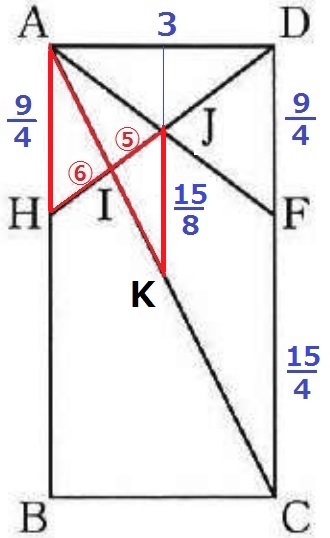
 △ＡＨＩ∽△ＫＪＩで、ＨＩ：ＪＩ＝９/４：15/８＝⑥：⑤
方針：【△ＡＨＤ⇒△ＡＨＪ⇒△ＡＩＪ】
△ＡＩＪの面積は、３×９/４÷２÷２×⑤/⑪＝135/176ｃｍ²

＠タレコミ＠

2015年の埼玉で類題があったそうです( ´ﾉω｀)ｺｯｿﾘ
このブログでも取り上げたのですが、すっかり忘れてました。。