2022年度　埼玉県公立高校入試・学校選択過去問【数学】解説

平均42.6点（前年比；－13.4点）

問題はコチラ→ＰＤＦファイル
2022年度・埼玉数学（共通問題）の解説はコチラ。

大問１（小問集合）

（１）　78.5％
６ｘｙ²÷（－３/５ｘｙ）÷（－２ｘ）³
＝６ｘｙ²÷（－３/５ｘｙ）÷（－８ｘ³）
＝５ｙ/４ｘ³

（２）　53.8％
√９＜√11＜√16だから、整数部分ａ＝３、小数部分ｂ＝√11－３
ａ²－ｂ²－６ｂ
＝ａ²－ｂ（ｂ＋６）　←代入
＝３²－（√11－３）（√11＋３）
＝９－11＋９＝７

（３）　78.9％
２（ｘ＋３）²－３（ｘ＋３）－３　←ｘ＋３＝Ｘとおく
＝２Ｘ²－３Ｘ－３＝０
ここで解の公式を適用すると、
Ｘ＝（３±√33）/４　←Ｘをｘ＋３に戻す
ｘ＋３＝（３±√33）/４
ｘ＝（－９±√33）/４

（４）　35.0％

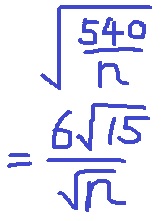
↑これが自然数になるようなｎは、15×（６の約数の平方数）
６の約数は〔１・２・３・６〕なので、ｎは４通り。
*具体的な数値でいえば、ｎ＝15×１^２＝15、15×２^２＝60、
15×３^２＝135、15×６^２＝540の４つ。

（５）　88.8％

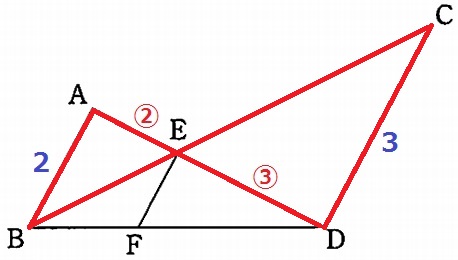
△ＡＢＥ∽△ＤＣＥより、ＡＥ：ＥＤ＝②：③

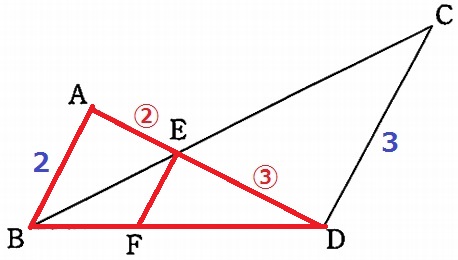
△ＡＢＤ∽△ＥＦＤで、ＥＦ＝２×③/⑤＝６/５ｃｍ

＠余談＠

受験業界では「和分の積」とよばれる形で、ＥＦ＝（２×３）/（２+３）＝６/５
ＡＢ＝３、ＣＤ＝７であれば、ＥＦ＝（３×７）/（３+７）＝21/10となる。

（６）　87.5％
高校から降りてきた箱ひげ図。

ｱｲ：四分位範囲は、上位グループの真ん中である第３四分位数（Q3）から、
下位グループの真ん中である第１四分位数（Q1）をひいた値。
極端な外れ値を除外するので、その影響を受けにくい。〇
ウ：平均は×印などで示す。箱の中央にあるとは限らない。×
エ：第２四分位数は中央値。〇
ウ

（７）　82.5％
印アリが③、印ナシが⑳、全体が㉓。
22匹が③に相当するので、総数は22×㉓/③＝506/３＝168.6…≒169匹

（８）　70.6％
歩いた時間をｘ分とすると、走った時間は24－ｘ分。
距離で等式を立てる。
50ｘ＋90（24－ｘ）＝1500
40ｘ＝660
ｘ＝16.5
16.5分＝16分30秒
走り始めた時刻は、午後１時16分30秒。

（９）　37.3％
なかなか興味深い問題です。

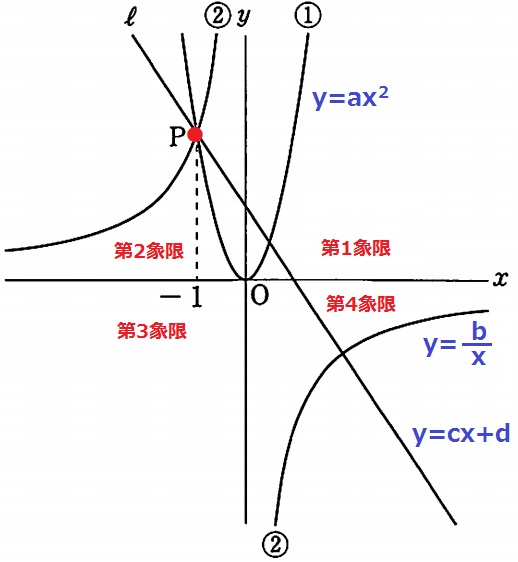
下に凸の放物線だからａ＞０
第２象限・第４象限に描かれる双曲線はｂ＜０
傾きが右下で、切片はｘ軸より上にある→ｃ＜０、ｄ＞０
ａ・ｄが正で、ｂ、ｃが負である。

手がかりになるのはＰの座標。
３つのグラフの交点なので３通りで表せる。
（－１、ａ）（－１、－ｂ）（－１、－ｃ＋ｄ）
ｙ座標は等しいから、ａ＝－ｂ＝－ｃ＋ｄ
●ａとｄの比較

注意点は、ｃ＜０なので－ｃは正の数である！
正のａは、正のｄに正の－ｃを足した数だからａ＞ｄ

●ｂとｃの比較

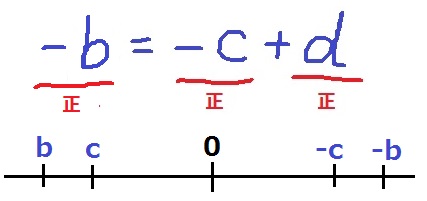
同様に、－ｂも正の数。
正の－ｂは、正の－ｃに正のｄを足した数だから－ｂ＞－ｃ
求めたいのはｂとｃの大小関係。
数直線で考えると、－ｂの方が－ｃより原点０から遠くにあるので、
マイナスをとって負に置き換えるとｂ＜ｃになる。
ｂ＜ｃ＜ｄ＜ａ

＠余談＠
－ｂ＞－ｃにマイナスをかけるとｂ＜ｃ
不等号の向きが逆になる。数Ⅰの一次不等式で習います。

（10）　8.6％！

さすが公式解答、手際が良い(;`ω´)
体積比は相似比の３乗。
ＳとＭの体積比と価格の比から、ＳよりＭが割安とわかる。
Ｍ：Ｌは半径の相似比４：５→底面積の比16：25→体積比16：50
価格の比に照らしてＭよりＬが割安だから、最も割安なのはＬサイズ。

連比で体積比を統一させることもできる。
１円あたりの体積比（27÷160…64÷320…200÷960）は計算が大変なので、
値段の比がＳ：Ｍ：Ｌ＝１：２：６と整っている点に気がつきたい。

大問２（作図・関数）

（１）　30.0％！
ＡＣ：ＡＢ＝１：√２
１や√２とくれば直角二等辺三角形。

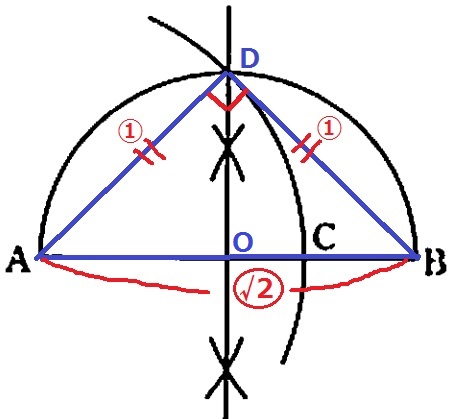
ＡＢを斜辺とする直角二等辺を想像する。
等辺①の長さをＡＢ上に移せばいい。
①ＡＢの垂直二等分線。
②ＡＢの中点Ｏから半径ＡＯをとって半円を描く。
①との交点をＤとすると△ＡＢＤは直角二等辺。
③ＡＤをＡＢ上に移してＣをとる。

（２）　6.9％!!

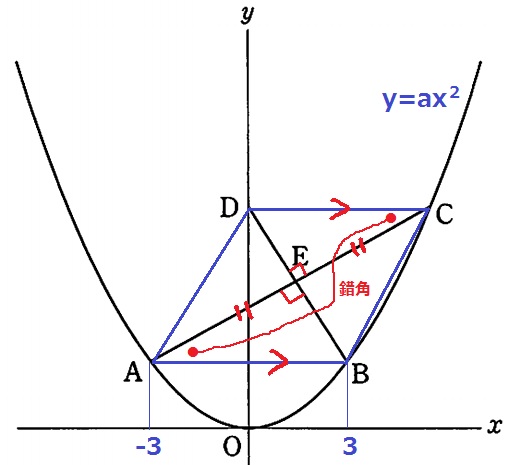
四角形で囲いたくなる気分…。
ＤはＣとｙ座標が等しい→ＤＣ//ＡＢ//x軸
ＡＥ＝ＣＥと錯角と垂直で、１辺両端角が等しく△ＡＢＥ≡△ＣＤＥ
対応する辺からＡＢ＝ＤＣ
１組の対辺の長さが等しくかつ平行→四角形ＡＢＣＤは平行四辺形。
さらに、対角線が各々の中点で垂直に交わる→四角形ＡＢＣＤは菱形。

ＤＣ＝ＡＢ＝６→Ｃのｘ座標は６。
Ｂ（３、９ａ）Ｃ（６、36ａ）
ＢＣ＝６を斜辺とする直角三角形ＢＣＦに着目する。
ＢＦ＝３、ＣＦ＝36ａ－９ａ＝27ａ
三平方より、ＣＦ＝√（６²－３²）＝３√３＝27ａ
ａ＝√３/９

大問３（確率）

（１）　47.5％

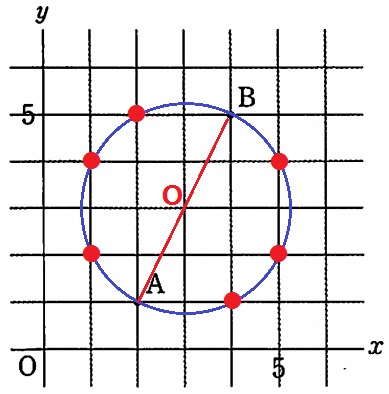
Ｋが「円の性質を利用する」と言うので、ＡＢを直径とする円を描いてみる。
半円の弧に対する円周角は90°で、Ａ・Ｂをのぞく格子点は６個ある。
確率は６/36＝１/６

（２）　43.6％

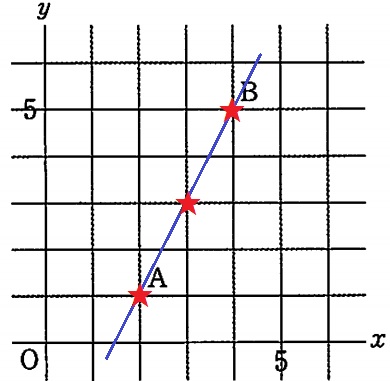
点ＰがＡＢ上にあると三角形ができない。
右に１、上に２だから傾きは２。
ｙ軸方向に直線を延長すると切片は－３。
ＡＢ；ｙ＝２ｘ－３

（２、１）（３、３）（４、５）の３個がバツ。
全体は６×６＝36通りだから、三角形ができるのは36－３＝33通り
ア…ｙ＝２ｘ－３、イ…33

（３）　0.7％!!!
答案では説明も記述する。

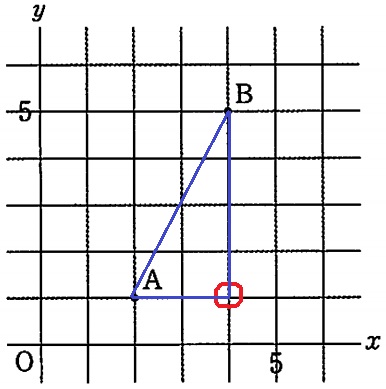
明らかに４ｃｍ²とわかる三角形から考える。
（４、１）の点に注目する。

これを通る傾き２の平行線をひく。
このライン上にＰがくると、等積変形で△ＡＢＰの面積はちょうど４ｃｍ²だから、
このラインを含む右側の点（ｘ、ｙ≦６）すべてが該当する。

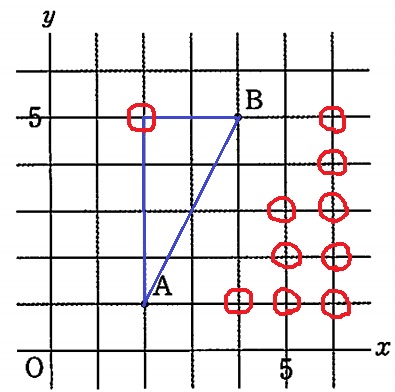
反対側で同じことをする。（２、５）に注目。

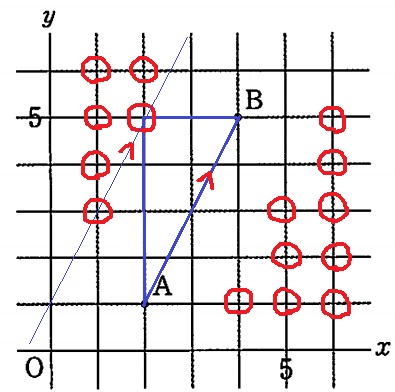
傾き２のラインを含む左側すべての点が該当。
４ｃｍ²以上となるのは15通りで、全体が33通りだから、
確率は15/33＝５/11

大問４（平面図形）

（１）　63.4％
ＰＡ＝ＰＢの証明。
円外の点Ｐからの接線の長さが等しいことを証明する。

△ＡＰＯと△ＢＰＯに注目する。
ＰＯは共通辺、半径よりＯＡ＝ＯＢ
半径と接線は垂直に交わるので、∠ＰＡＯ＝∠ＰＢＯ＝90°
斜辺と他の１辺が等しい直角三角形ゆえ△ＡＰＯ≡△ＢＰＯ
対応する辺は等しいから、ＰＡ＝ＰＢ

（２）　6.9％!!

半径を作図し、ＰとＲとＱを結ぶ。
ＲＯ＝ＲＱ＋ＱＯ＝３＋５＝８ｃｍ

円Ｒと直線ℓの接点をＤとする。
△ＰＲＤ∽△ＰＯＡで、相似比はＲＤ：ＯＡ＝３：５
ＰＲ＝８×３/２＝12ｃｍ

ＰＤ：ＤＡ＝③：②
点Ｃをどうするか。。

内接円の問題で見たことがあると思う。
★ペアと＠ペアの三角形は（１）の証明と同様の理由で合同。
ＤＣ＝ＱＣ＝ＡＣ
ＤＣ＝②÷２＝①

△ＰＲＤで三平方→ＰＤ＝３√15ｃｍ
ＰＣ＝３√15×④/③＝４√15ｃｍ

＠余談＠

本問と全然関係ないんですけど、中学レベルの数学で解ける慶應大学の問題です。
ぜひチャレンジしてみてください。
答えは下の『』内をドラッグしてください。
円Ｂの半径…『４＋２√５』
円Ｈの半径…『18＋８√５』

大問５（空間図形）

（１）　42.2％
球の体積は４/３πｒ³
立体Ｖは球の８分の１なので、４/３πｒ³×１/８＝π/６ｒ³ｃｍ³

（２）　4.0％!!
答案では説明も記述する。

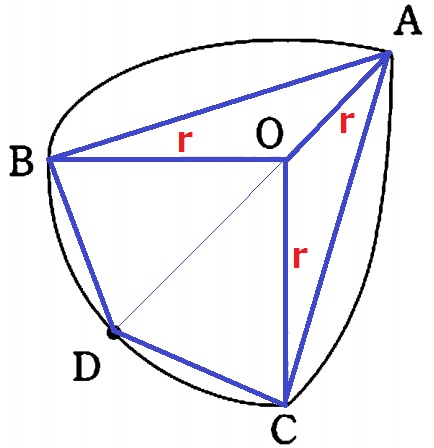
四角錘の高さはＡＯ＝ｒｃｍ
あとは底面にあたる四角形ＯＢＤＣの面積を出せばいい。

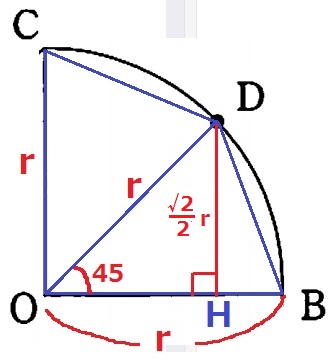
ＯＤに補助線。
Ｄは弧ＢＣの中点→∠ＤＯＢ＝45°
Ｄから垂線をおろし、足をＨとする。
△ＯＤＨの内角は45°―45°―90°だから直角二等辺三角形。
辺の比は１：１：√２なので、ＤＨ＝ｒ×１/√２＝√２/２ｒｃｍ
対称性から、△ＢＯＤ×２＝四角形ＯＢＤＣ
四角錘の体積は、ｒ×√２/２ｒ÷２×２×ｒ÷３＝√２/６ｒ³ｃｍ³

（３）　0.3％!!!
これは諦めるしかない(ﾉ∀`)

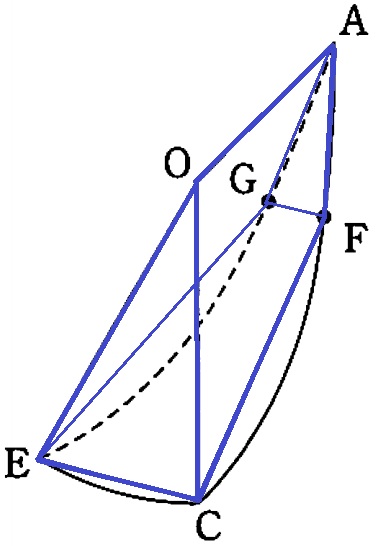
△ＯＣＥと△ＡＦＧは平行な面ではない。
手がかりは∠ＣＯＥ＝30°と弧を１：２に内分するＧ・Ｆしかないという…。

ＯＡ・ＥＧ・ＣＦを延長、交点をＨとする。
右図は△ＯＨＣ側から見た図でＡＦは傾いているが、
三角錐Ｈ―ＯＣＥとの体積比から立体ＡＦＧ―ＯＣＥの体積の算出を試みる。

ＯＦに補助線。
弧ＡＦ：弧ＦＣ＝１：２より、∠ＡＯＦ＝30°、∠ＦＯＣ＝60°
△ＯＦＣは１辺ｒの正三角形で、△ＯＨＦは２つの底角を30°とする二等辺三角形。
ＣＦ＝ＦＨ＝ｒ
△ＯＨＣは内角が30°―60°―90°で辺の比は１：２：√３だから、ＯＨ＝√３ｒ
ＡＨ＝√３ｒ－ｒ＝（√３－１）ｒ

隣辺比から体積比を求める。
三角錐Ｈ―ＯＣＥ…ＨＯ×ＨＣ×ＨＥ＝√３ｒ×２ｒ×２ｒ＝４√３ｒ³
三角錐Ｈ―ＡＦＧ…ＨＡ×ＨＦ×ＨＧ＝（√３－１）ｒ×ｒ×ｒ＝（√３－１）ｒ³
立体ＡＦＧ―ＯＣＥ…４√３ｒ³－（√３－１）ｒ³＝（１＋３√３）ｒ³
ｒだらけで目まいがする⊂(^ω^)⊃

うえのように△ＯＥＣ内で30°―60°―90°の直角三角形をつくると、底辺がｒ、高さが１/２ｒ
三角錐Ｈ―ＯＣＥの体積は、ｒ×１/２ｒ÷２×√３ｒ÷３＝√３/12ｒ³
したがって、求積すべき立体の体積は、√３/12ｒ³×｛（１＋３√３）ｒ³｝/４√３ｒ³
＝（１＋３√３）/48ｒ³

・・たぶん、これは試験時間内には終わらないことを想定して、
お家で楽しんでくださいっていう埼玉教委会からのお土産なんだと思う。

＠別解＠

立体を錘に分割して、（２）のように断面積×高さ÷３で求めることもできる。
この場合、面ＡＥＦの前後で分ける。
四角形ＯＡＦＣの面積…ｒ×１/２ｒ÷２＋ｒ×√３/２ｒ÷２＝（１＋√３）/４ｒ²
四角錘Ｅ―ＯＡＦＣの体積…（１＋√３）/４ｒ²×１/２ｒ÷３＝（１＋√３）/24ｒ³

△ＡＧＥは、四角形ＯＡＧＥから直角二等辺ＯＡＥを引けばいい。
△ＡＧＥの面積…（１＋√３）/４ｒ²－ｒ×ｒ÷２＝（√３－１）/４ｒ²
高さは垂線をひき、ＯＥの半分がＨＧとわかれば、
これを立体に引きなおして、１/２ｒ÷２＝１/４ｒ
三角錐Ｆ―ＡＧＥの体積…（√３－１）/４ｒ²×１/４ｒ÷３＝（√３－１）/48ｒ³
求積すべき立体の体積は、（１＋√３）/24ｒ³＋（√３－１）/48ｒ³＝（１＋３√３）/48ｒ³

＠＠＠＠
以下、埼玉県から発表された解法です。

△ＯＣＥと平行な△ＨＦＧで立体を分割しています。
１：２：√３の直角三角形を頼りに、先端の三角錐が（２－√３）/96ｒ³

残りの三角錐の一部（錐台）で、三角錐×７/８＝７√３/96ｒ³
これらを足すと（１＋３√３）/48ｒ³
現場でこれを当てた子は見事です。おめでとうございました。