2022年度　神奈川県公立高校入試・追検査過去問【数学】解説

問題はコチラ→ＰＤＦファイル
2022年度・神奈川本試験（数学）の解説はコチラ。

大問１（計算）

（ア）
－４－（－９）
＝－４＋９
＝５　【３】

（イ）
１/４－３/７
＝－５/28　【２】

（ウ）
72ａ²ｂ÷４ａ×３ｂ
＝54ａｂ²　【４】

（エ）
（４ｘ－３ｙ）/５－（ｘ－ｙ）/２
＝｛２（４ｘ－３ｙ）－５（ｘ－ｙ）｝/10
＝（８ｘ－６ｙ－５ｘ＋５ｙ）/10
＝（３ｘ－ｙ）/10　【２】

（オ）
（１－√５）（１＋√５）－２（３－√５）
＝１－５－６＋２√５
＝－10＋２√５　【１】

大問２（小問集合）

（ア）
（ｘ－７）²＋３（ｘ－７）－28　←ｘ－７＝Ｘとおくと…
＝Ｘ²＋３Ｘ－28
＝（Ｘ＋７）（Ｘ－４）　←ここでＸをｘ－７に戻す
＝ｘ（ｘ－11）　【３】

（イ）
３ｘ²＋２ｘ－２＝０
解の公式。ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝（－１±√７）/３　【１】

（ウ）
ｘ＝－１のとき、ｙ＝ａ
ｘ＝－３のとき、ｙ＝９ａ
変化の割合…（ｙの増加量）÷（ｘの増加量）
＝（ａ－９ａ）/｛－１－（－３）｝＝－８ａ/２＝－４ａ＝３
ａ＝－３/４　【２】

＠別解＠
ｙ＝ａｘ²において、ｘの値がｐからｑに増加するときの変化の割合はａ（ｐ＋ｑ）。
（－３－１）ａ＝－４ａ＝３
ａ＝－３/４

（エ）
加える量をｘｍＬとすると、
紅茶：ミルク＝360＋ｘ：200＋ｘ＝５：３
内項と外項の積で、５（200＋ｘ）＝３（360＋ｘ）
２ｘ＝80
ｘ＝40
40ｍＬ　【３】

＠別解＠
算数の世界では、以下のように解きます。

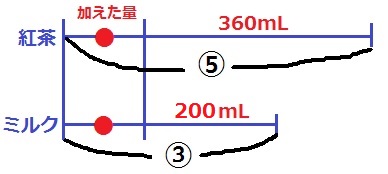
加えた量を左側に寄せた線分図を描きます。

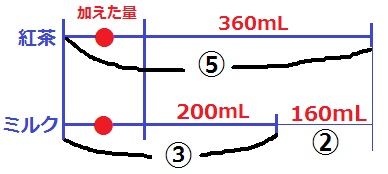
差の②＝160ｍＬだから、ミルクは160×③/②＝240ｍＬ
加えた量は、240－200＝40ｍＬ

（オ）

３ｎは55未満でなくてはならない。
整数となる⇒根号を外すには、根号の中身が平方数になる。
55未満の平方数は【１・４・９・16・25・36・49】。

３ｎは３の倍数、55は３の倍数＋１。
３の倍数＋１から３の倍数をひいたら、差は３の倍数＋１になる。
先の平方数のなかで該当するのは【１・４・16・25・49】の５個。　【４】
*具体的な値でいえば、ｎ＝２、10、13、17、18

大問３（小問集合２）

（ア）ⅰ
△ＡＥＣ∽△ＥＧＦの証明。

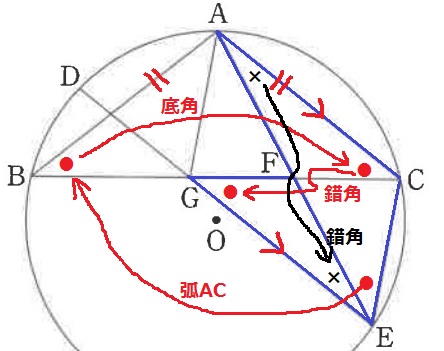
ＡＣ//ＤＥの錯角、二等辺三角形ＡＢＣの底角、弧ＡＣに対する円周角。
これらを駆使して２角相等で∽。
ａ…【２】、ｂ…【３】

ⅱ
追試験の最難関。パス推奨です。

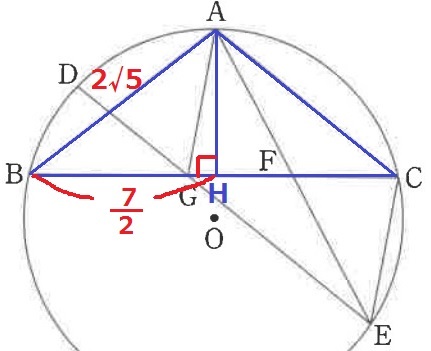
面積比ではなく面積を求めよなので、とりあえず高さを出してみる。。
Ａから垂線、足をＨとする。
△ＡＢＣは二等辺三角形だから、ＢＨ＝７/２ｃｍ
△ＡＢＨで三平方→ＡＨ＝√31/２ｃｍ
この後どうしよう(´°ω°`;)

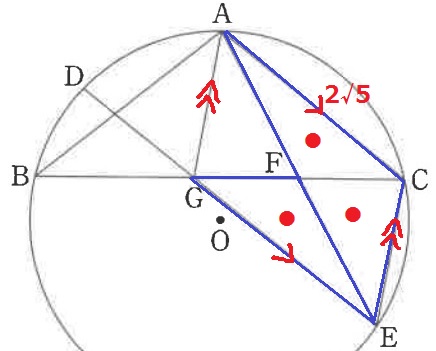
前問の相似に目を向けてみる。
四角形ＡＧＥＣは２組の対辺が平行だから平行四辺形。
平行四辺形は対角線で面積が４等分される。
ということは、●の部分が等積なので△ＡＥＣ：△ＥＧＦの面積比は２：１。
相似比は√２：１。
ＡＣに対応する辺ＥＦ＝２√５×１/√２＝√10ｃｍ

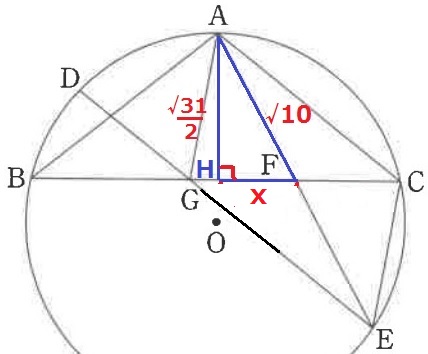
平行四辺形の対角線は各々の中点で交わるから、ＡＦ＝ＦＥ＝√10ｃｍ
△ＡＦＨで三平方。
ＨＦ²＝（√10）²－（√31/２）²
＝10－31/４＝９/４
ＨＦ＞０だから、ＨＦ＝３/２ｃｍ

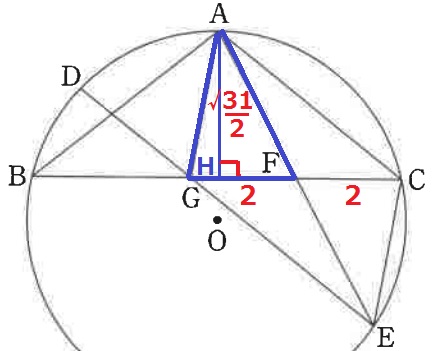
ＦＣ＝７/２－３/２＝２ｃｍ
平行四辺形の対角線より、ＧＦ＝ＦＣ＝２ｃｍ
したがって、△ＡＧＦの面積は、２×√31/２÷２＝√31/２ｃｍ²

（イ）
５日間の総和は、17＋27＋19＋27＋31＝121回
６日間の平均値は（121＋α）÷６だが、121÷６だけで20を超えるので、
平均値が20回になることはない→Ａ×
平均値が30回のとき、総和は30×６＝180回
121回を超えるので、平均値30回はありうる→Ｅ〇
（*６日目は59回となる）

昇順に並び替えると【17・19・27・27・31】。
６個の中央値は３番目と４番目の平均。
６日目が23回であれば、中央値は23と27回の平均で25回となる→Ｂ〇
27が３番目と４番目にあるので、中央値29回はありえない→Ｄ×

問題はＣ。
最も中央値にしやすいのが27回なので、
仮に平均値を27回とすると、６日間の総和は27×６＝162回
５日目までの総和121回を超えるのでありえる→Ｃ〇
（*６日目は41回となる）
Ｂ・Ｃ・Ｅ　【７】

（ウ）
一筋縄ではいかない。
共通問題のように、おそらく等角の大きさがわからないと出ない。
36°と28°を有効活用できそうな補助線を見つける。

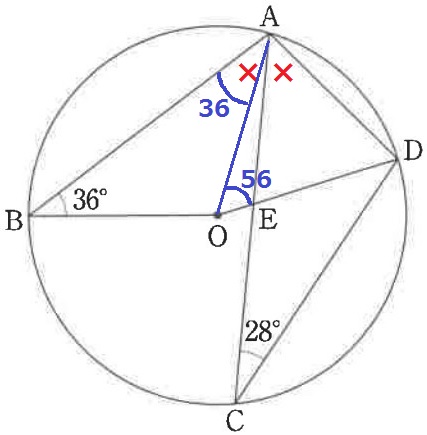
ＡＯに補助線。
半径より△ＡＯＢは二等辺三角形→∠ＯＡＢ＝36°
中心角は円周角の２倍だから、∠ＡＯＤ＝28×２＝56°

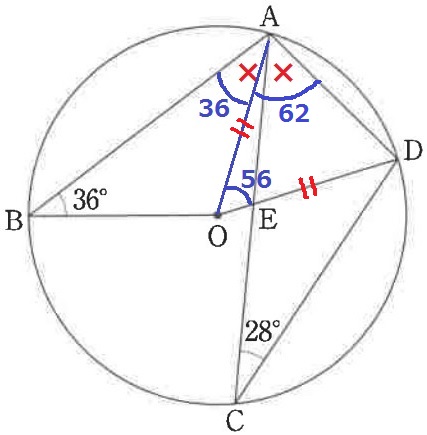
△ＯＡＤも同様に二等辺で、∠ＯＡＤ＝（180－56）÷２＝62°
×＝（36＋62）÷２＝49°

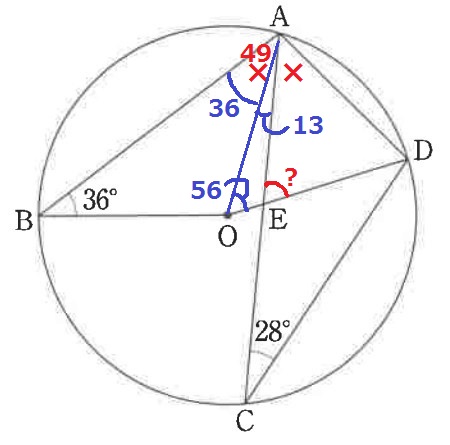
∠ＯＡＥ＝49－36＝13°
最後に△ＯＡＥで外角定理→∠ＡＥＤ＝56＋13＝69°

（エ）ⅰ

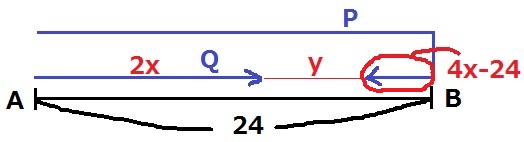
ＰがＢを折り返した６秒後以降を考える。
Ｐの移動距離は４ｘ。これに片道分をのぞいた４ｘ－24。
Ｑの移動距離は２ｘ。
あいだの距離ｙ＝24－（４ｘ－24＋２ｘ）＝－６ｘ＋48　【８】

＠別解＠

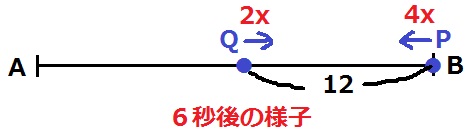
Ｐが折り返す６秒後の様子をとらえる。
速さの比がＰ：Ｑ＝２：１なのでＱはＡＢの中点にいて、ＰとＱは12ｃｍ離れている。
ここから４ｘ＋２ｘ＝６ｘごとに距離をつめていくから、グラフの傾きは－６ｘ。
ｙ＝－６ｘ＋ｂに（ｘ、ｙ）＝（６、12）を代入。
12＝－６×６＋ｂ
ｂ＝48
ｙ＝－６ｘ＋48

ⅱ
前問の式にｙ＝０を代入。
―６ｘ＋48＝０
ｘ＝８　【２】

＠余談＠
値だけを求めるならば、算数で一瞬です(;^ω^)

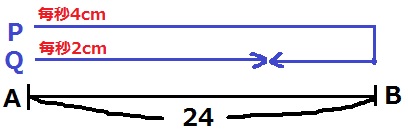
出会うまでにＰとＱが移動した距離の合計は往復の48ｃｍ。
48ｃｍ離れている状態でＰとＱが接近していく。
１秒間に４＋２＝６ｃｍずつ近づくので、48÷６＝８秒後

大問４（関数）

（ア）
Ａのｘ座標は７。
ｙ＝ｘ上の点だから、Ａ（７、７）
これをｙ＝ａｘ²に代入。
７＝49ａ
ａ＝１/７　【１】

（イ）

ＡＥ：ＥＢ＝２：５
ＡとＢは14離れているので、２倍して４：10にするとちょうど和が14になる。
Ｅ（３、７）
ＤＯ：ＯＧ＝７：５はＤＯ＝７から、そのまま長さとして扱える。
Ｇ（－５、０）

Ｇ（－５、０）⇒Ｅ（３、７）
右に８、上に７だから傾きは７/８。

傾き７/８より、ＧＯとＯ～切片までの比が⑧：⑦。
切片は、５×⑦/⑧＝35/８
ｙ＝７/８ｘ＋35/８
ⅰ…【５】、ⅱ…【４】

（ウ）

奇妙なところが等積らしい(;`ω´)
面積比を地道に調べていく。
ゴールがＨのｘ座標なので、先にＯＦを使いそう。

△ＯＦＤ∽△ＥＦＣより、ＥＦ：ＦＯ＝③：⑦
△ＯＡＦの面積を⑦とすると、△ＦＡＥ＝③、△ＯＨＢ＝⑦
△ＯＡＥ：△ＯＥＢ＝ＡＥ：ＥＢ＝２：５
△ＯＥＢ＝⑩×５/２＝㉕
△ＨＥＢ＝㉕－⑦＝⑱

ＯＨ：ＨＥ＝⑦：⑱だから、Ｈのｘ座標は３×⑦/㉕＝21/25

大問５（確率）

（ア）
ルールが複雑系(;°;ω;°;)

上からルール①、②、③とする。
11枚残るということは、取り除くカードを２枚にする。
●ルール①
出目の最大数である（６、６）を出しても６以上の素数は【７・11・13】だから、
どう頑張っても３枚取り除かれるのでナシ。
●ルール②
【10・12】だけを取り除くようにする。
ａ＋ｂ以上の偶数なので９はセーフ。８だと【８】も取り除かれるので×。
11だと【10】を取り除けないので×。
９≦ａ＋ｂ≦10、ａ＜ｂ
（ａ、ｂ）＝（３、６）（４、５）（４、６）の３通り。
●ルール③
【11・13】だけを取り除きたいが、最大出目が６なので【７・９】も取り除かれる。
無し！

全体は６×６＝36通り
確率は３/36＝１/12

（イ）
６枚を取り除く。
●ルール①
２以上（すべて）の素数を取り除く。
１≦ａ≦２
（ａ、ｂ）＝（１、１）（２、２）の２通り。
●ルール②
２以上（すべて）の偶数を取り除く。
１≦ａ＋ｂ≦２、ａ＜ｂ
該当するａとｂのペアは無い。
●ルール③
３以上の奇数を取り除く。
２≦ｂ≦３、ａ＞ｂ
ｂ＝２のとき、ａ＝３～６の４通り。
ｂ＝３のとき、ａ＝４～６の３通り。

計９通り。
確率は９/36＝１/４

大問６（空間図形）

（ア）

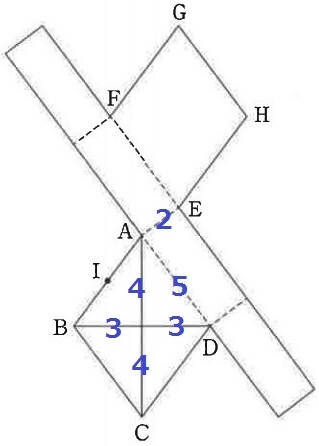
３：４：５より、ＡＤ＝５ｃｍ
菱形の面積は〔対角線×対角線÷２〕だから、
立体の表面積は、６×８÷２×２＋２×５×４＝88ｃｍ²　【４】

（イ）

展開図ではなく、立体におけるＧＩ間の距離を求める。
立体のナナメ線は、それを対角線とする直方体を想像する。
１辺がａ、ｂ、ｃの直方体の対角線の長さ→√（ａ²＋ｂ²＋ｃ²）
高さ２ｃｍがわかっているので、上から見たときの縦と横の長さが知りたい。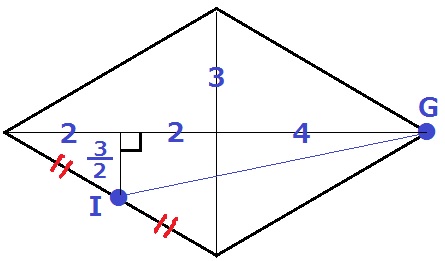
Ｉが中点であることを利用して、横が６ｃｍ、縦が３/２ｃｍ。
したがって、ＧＩ＝√｛６²＋（３/２）²＋２²｝＝√（169/４）＝13/２ｃｍ　【６】

（ウ）

最短距離なので展開図。
与えられた図の菱形をゴロンと転がす。

交点をＪ・Ｋとする。
菱形の面積は24ｃｍ²なので、底辺５ｃｍで割れば高さＢＪ（ＫＦ）が出る。
ＢＪ＝ＫＦ＝24/５ｃｍ
ＢＦ＝24/５×２＋２＝58/５ｃｍ

＠2022年度・神奈川解説＠
数学…平均52.9点　社会…平均62.4点　理科…平均58.9点　英語…平均52.1点
公立高校入試解説ページに戻る