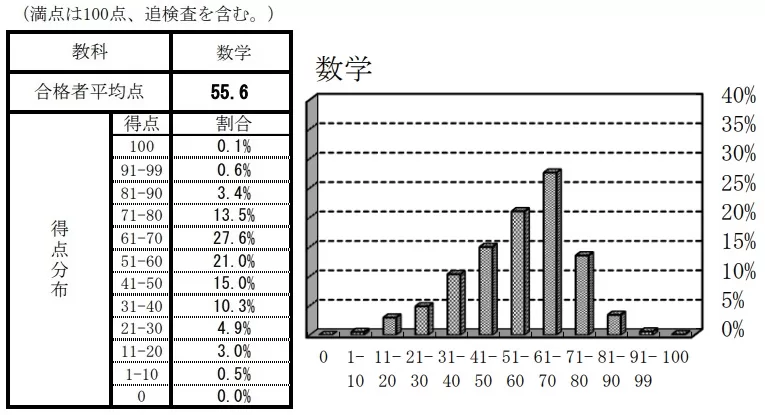
平均55.6点（前年比；＋2.6点）
問題はコチラ→ＰＤＦファイル
大問１（計算）
（ア） 98.0％
２－８
＝－６ 【２】
（イ） 97.7％
－４/５＋１/４
＝－11/20 【２】
（ウ） 89.2％
（３ｘ－ｙ）/４－（５ｘ＋２ｙ）/９
＝｛９（３ｘ－ｙ）－４（５ｘ＋２ｙ）｝/36
＝（27ｘ－９ｙ－20ｘ－８ｙ）/36
＝（７ｘ－17ｙ）/36 【１】
（エ） 94.8％
10/√５＋√80
＝２√５＋４√５
＝６√５ 【３】
（オ） 91.9％
（ｘ－２）2－（ｘ＋３）（ｘ－８）
＝ｘ2－４ｘ＋４－（ｘ2－５ｘ－24）
＝ｘ2－４ｘ＋４－ｘ2＋５ｘ＋24
＝ｘ＋28 【４】
大問２（小問集合）
（ア） 89.6％
ｘ＝３、ｙ＝２を代入。
３ａ－２ｂ＝－10 …①
２ａ＋３ｂ＝－11 …②
①×２－②×３をすると、－13ｂ＝13
ｂ＝－１
①に代入。３ａ－２×（－１）＝－10
３ａ＝－12
ａ＝－４ 【２】
（イ） 90.9％
３ｘ2－５ｘ－１＝０
解の公式を適用すると、ｘ＝（５±√37）/６ 【４】
（ウ） 69.8％
０≦ｙ≦６→ａ＞０（グラフは下に凸のグラフ）
ｘ＝－３のとき、最大値ｙ＝６
これらをｙ＝ａｘ2に代入すると、
６＝９ａ
ａ＝２/３ 【１】
（エ） 76.5％
ペンの合計…150ｘ円、ノートの合計…200ｙ円
これらの和が3000円以下だから、150ｘ＋200ｙ≦3000 【３】
（オ） 55.8％
【球の体積Ｖ＝４/３πｒ3】
４/３π×６3＝288πｃｍ3 【４】
（カ） 86.2％
ｘ2－９ｙ2 ←平方の差
＝（ｘ＋３ｙ）（ｘ－３ｙ）
＝（143＋３×47）（143－３×47）
＝（143＋141）（143－141）
＝284×２＝568 【３】
大問３（小問集合２）
（ア）ⅰ ａ…92.6％、ｂ…90.7％
△ＡＣＧ∽△ＡＤＨの証明。
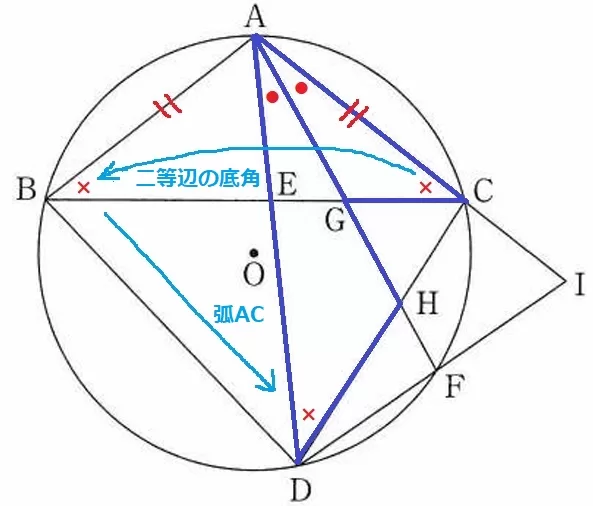
仮定の二等分線より、∠ＣＡＧ＝∠ＤＡＨ
ＡＢ＝ＡＣより△ＡＢＣは二等辺三角形。
２つの底角は等しいから、∠ＡＢＣ＝∠ＡＣＢ
弧ＡＣに対する円周角で、∠ＡＢＣ＝∠ＡＤＣ
よって、∠ＡＣＧ＝∠ＡＤＨ
２角が等しいので∽。
ａ…【１】、ｂ…【４】
ⅱ 12.8％！
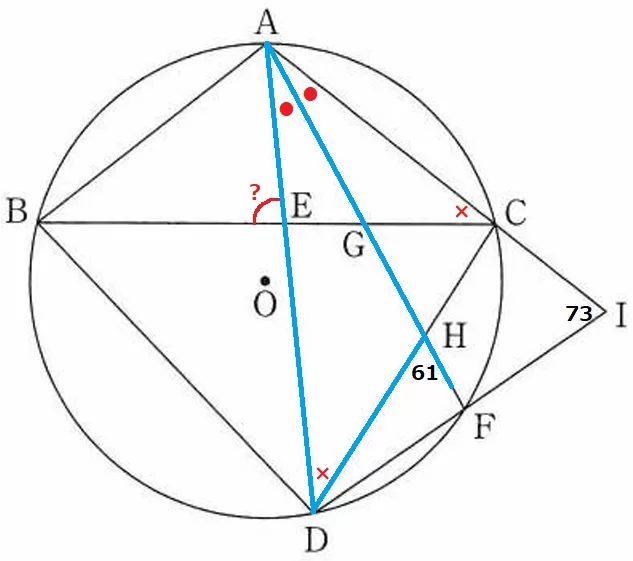
先ほどの等角を足掛かりにする。
△ＡＤＨで外角定理より、●＋×＝61°
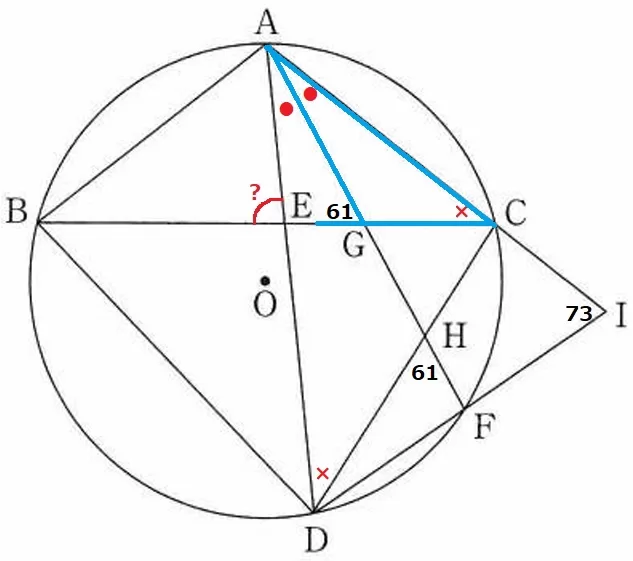
△ＡＧＣの外角定理から、∠ＡＧＥ＝●＋×＝61°
同様に△ＡＥＧの外角定理で、∠ＡＥＢ＝●＋61°である。
●が知りたい。
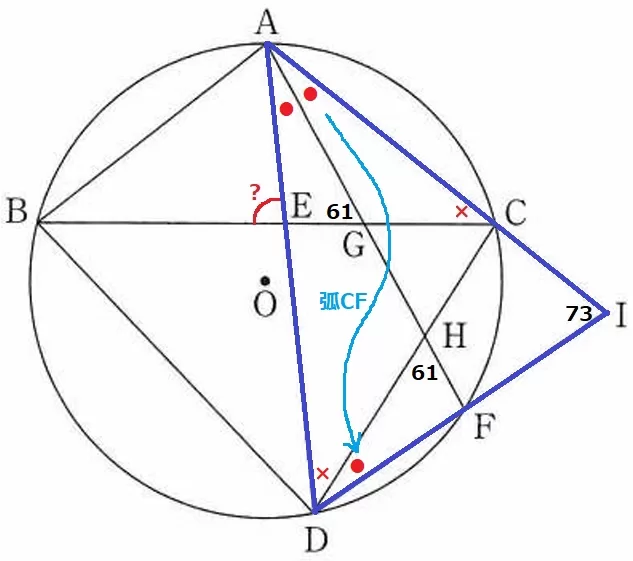
弧ＣＦの円周角より、∠ＣＤＦ＝●
△ＡＤＩの内角に着目する。
●＋●＋（●×）＋73＝●＋●＋61＋73＝180
●●＝46°
●＝23°
したがって、∠ＡＥＢ＝23＋61＝84°
＠別解＠
0ystarさんから素敵な別解をいただきました。
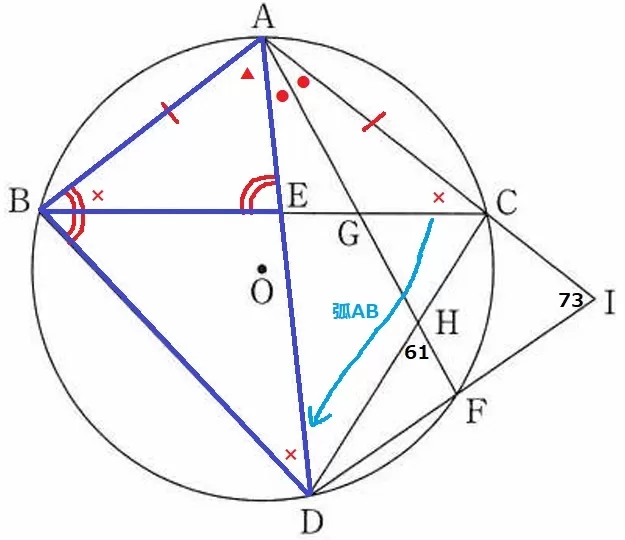
∠ＡＢＥ＝∠ＡＤＢ（×）、共通角（▲）より△ＢＡＥ∽△ＤＡＢです。
対応する角から、∠ＡＥＢ＝∠ＡＢＤ
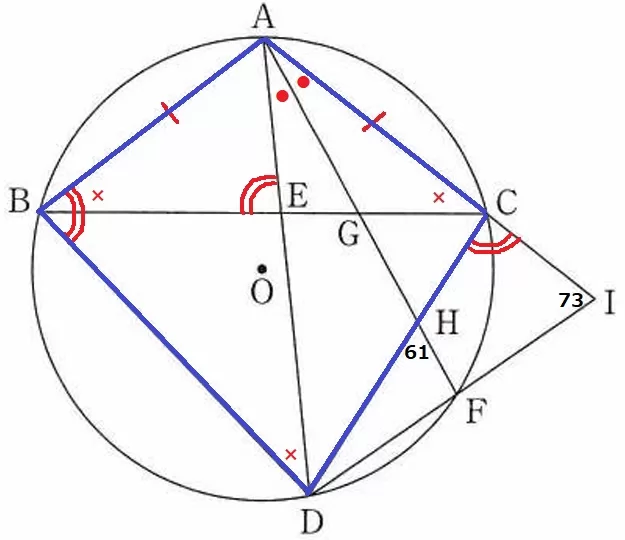
円に内接する四角形の内角は、その対角の外角に等しいので、
∠ＡＢＤ＝∠ＩＣＤ
求めるべき角を右側に移動できました。
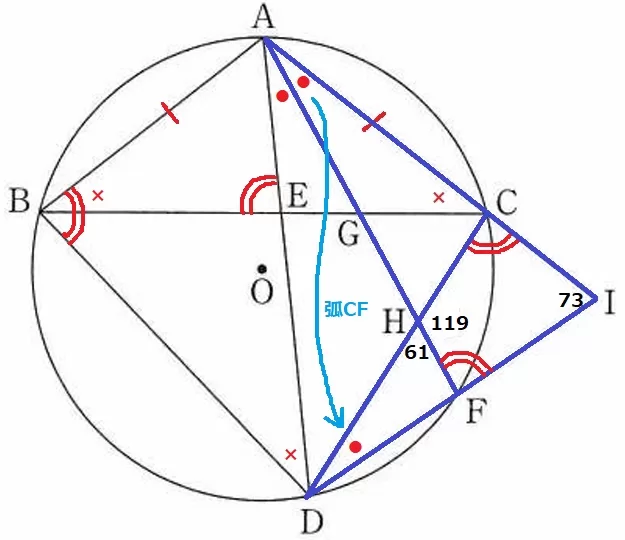
∠ＣＡＦ＝∠ＣＤＦ（●）と共通角73°より△ＡＩＦ∽ＤＩＣ。
対応する角で、∠ＩＣＤ＝∠ＩＦＡ
∠ＣＨＦ＝180－61＝119°
四角形ＣＩＦＨの内角より、∠ＡＥＢ＝（360－119－73）÷２＝84°
（イ）ⅰ 57.8％
ＡＢは50人。
中央値（Q2）…25番目と26番目の平均。
第３四分位数（Q3）…上位25人の真ん中、上から13番目。
第１四分位数（Q1）…下位25人の真ん中、下から13番目。
Ｃは60人。
Q2は30番目と31番目の平均。
Q3は上から15番目と16番目、Q1は下から15番目と16番目の平均。
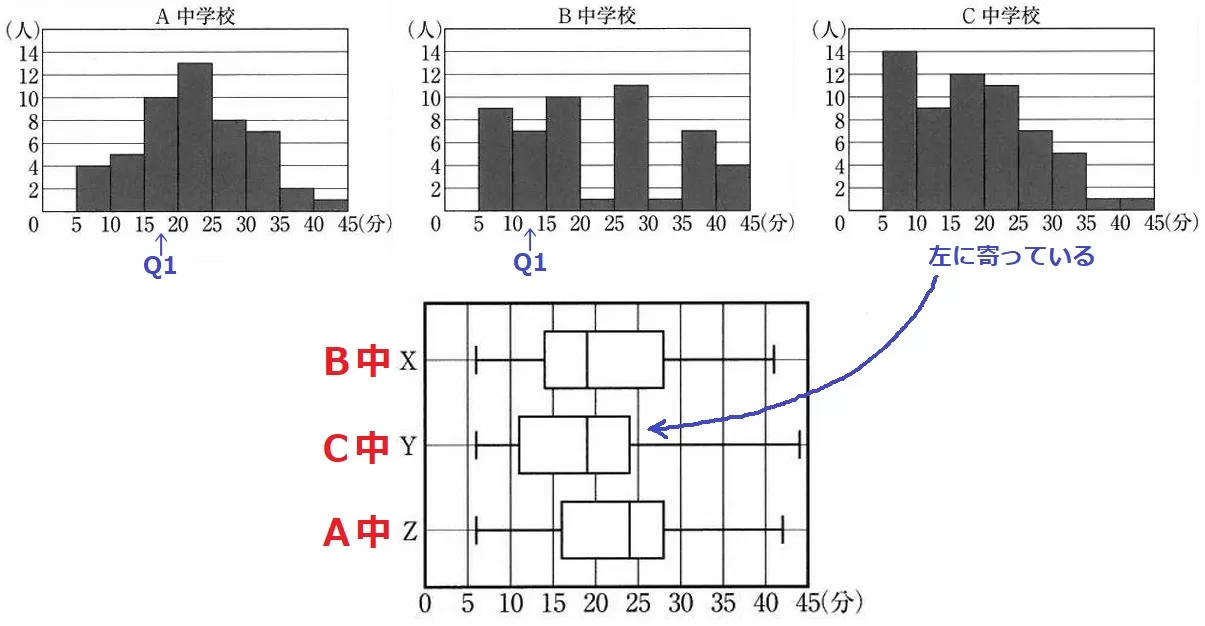
最も見当がつきやすいのはＣ中。
ヒストグラム全体が左に寄っているので、真ん中付近の50％である箱も左に寄るはず。
Ｃ中のＱ3を調べてみると、唯一20～25分の階級に含まれる。
残りはQ1の違いから判断して、ＡとＢの下から13番目を調べるとすべて決まる。【４】
ⅱ 33.4％
ヒストグラムから判断する。
Ⅰ：30分以上はＢ中の１＋７＋４＝12人が最多。×
Ⅱ：Ａ中…５/50、Ｂ中…７/50、Ｃ中…９/60
通分で比較すると、７/50＜９/60だからＣ中が最も大きい。×
Ⅲ：Ａ中…10/50、Ｂ中…10/50、Ｃ中…12/60→いずれも１/５で等しい。〇
Ⅳ：25分の境をつくると、Ａ中とＣ中は左が多いので均すと25分未満になる。
Ｂ中はいったん27.5分の境で判断すると、20～35分までは左右対称で平均値27.5分。
残りの青枠を考慮すると、平均値は－2.5分を超える（＝25分未満）と判断できる。〇【６】
（ウ） 3.4％!!
面白い問題です。
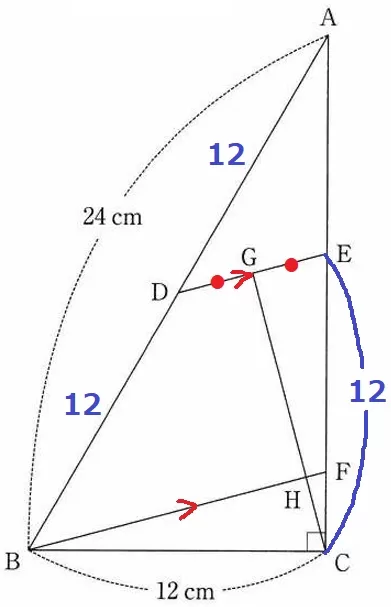
取っ掛かりがつかみにくい。
一番奇妙な情報はどこかといえば、ＥＣ＝12ｃｍ
12ｃｍが目につくので、これをどうにか活用したい。
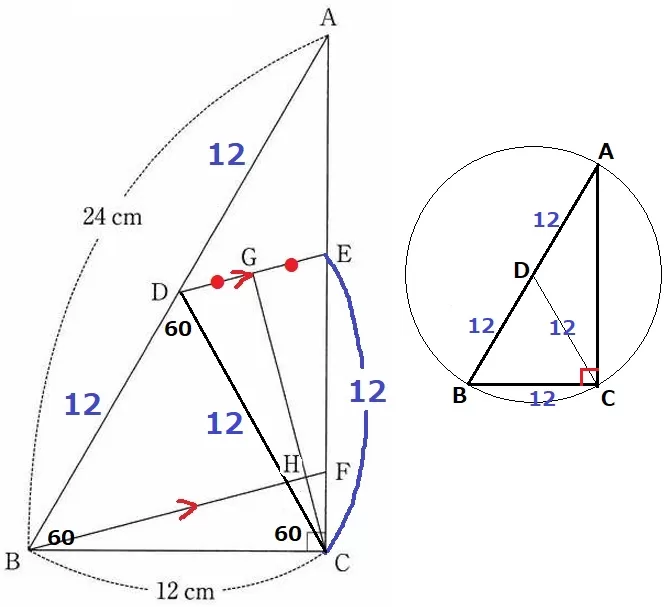
直角三角形の斜辺の中点Ｄを中心とする円を想像する。
直径ＡＢに対する円周角∠ＡＣＢ＝90°→半径よりＤＣ＝12ｃｍ
△ＢＣＤは３辺が等しい正三角形である。
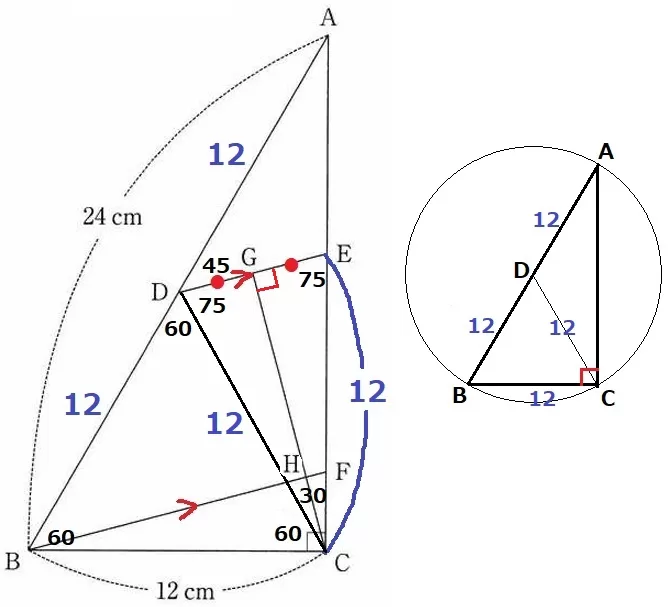
角度を調べていく。
∠ＤＣＥ＝90－60＝30°
△ＣＥＤは二等辺三角形なので、∠ＣＤＥ＝（180－30）÷２＝75°
ＣＧは底辺ＤＥの中点を通る→ＣＧ⊥ＤＥ
∠ＡＤＥ＝180－（60＋75）＝45°
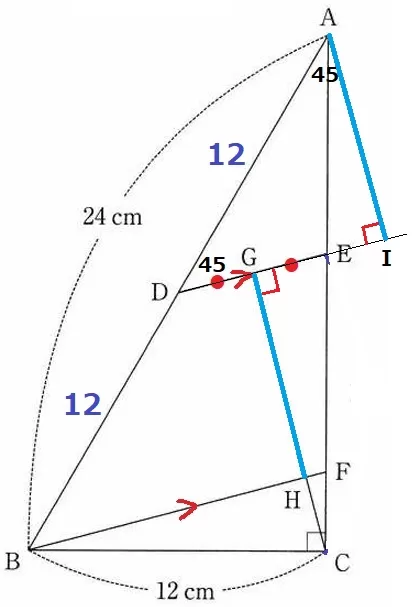
求めたいのはＧＨの長さ。
ＤＥ//ＢＦに注目すると、ＧＨは平行線の距離に相当する。
ＤＥを延長して、Ａからおろした垂線の足をＩとする。
ＡＤ：ＤＢ＝１：１より、ＡＩ＝ＧＨ
△ＡＤＩの内角は45°―45°―90°の直角二等辺三角形。
辺の比は１：１：√２だから、ＡＩ＝ＧＨ＝12×１/√２＝６√２ｃｍ
（エ） 18.6％！
最初の塩は、300×４％＝12ｇ
ａｇの食塩水を取り出して、ａｇの食塩を入れたから、食塩水全体は300ｇで変わらない。
最後の塩は、300×12％＝36ｇ
つまり、塩は24ｇ増えている。
取り除いた食塩水ａｇの濃度は４％。ａを【100】とすると、これに含まれる塩の量は【４】。
入れたａｇの塩は濃度100％だから【100】。
増加した塩の量で等式を立てると、－【４】＋【100】＝【96】＝24ｇ
ａ＝24×【100】/【96】＝25ｇ 【５】
大問４（関数）
（ア） 89.1％
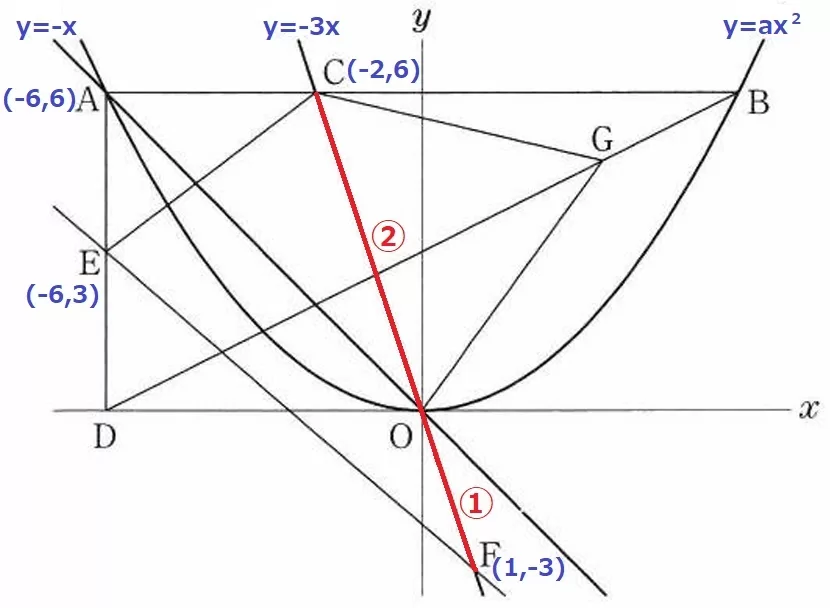
ｙ＝－ｘにｘ＝－６を代入→Ａ（－６、６）
これをｙ＝ａｘ2に代入すると、
６＝36ａ
ａ＝１/６ 【２】
（イ） 69.1％
Ｃのｙ座標はＡと同じ６。
ｙ＝－３ｘにｙ＝６を代入→Ｃ（－２、６）
ＣＯ：ＯＦ＝②：①より、Ｆ（１、－３）
Ｅ（－６、３）→Ｆ（１、－３）
右に７、下に６なので、傾きｍは－６/７
Ｆ（１、－３）から左に１、上に６/７移動して、切片ｎは－３＋６/７＝－15/７
ⅰ…【５】、ⅱ…【３】
（ウ） 6.0％!!
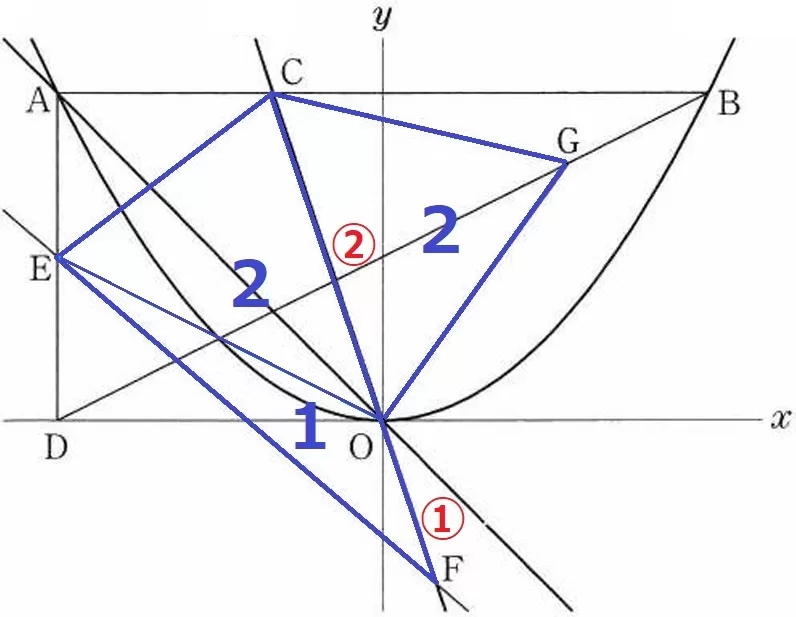
△ＣＥＦ：△ＣＯＧ＝３：２
ＣＯ：ＯＦ＝②：①に着目して△ＣＥＦをＥＯで分割すると、
△ＣＥＯと△ＣＯＧは面積２で等積。
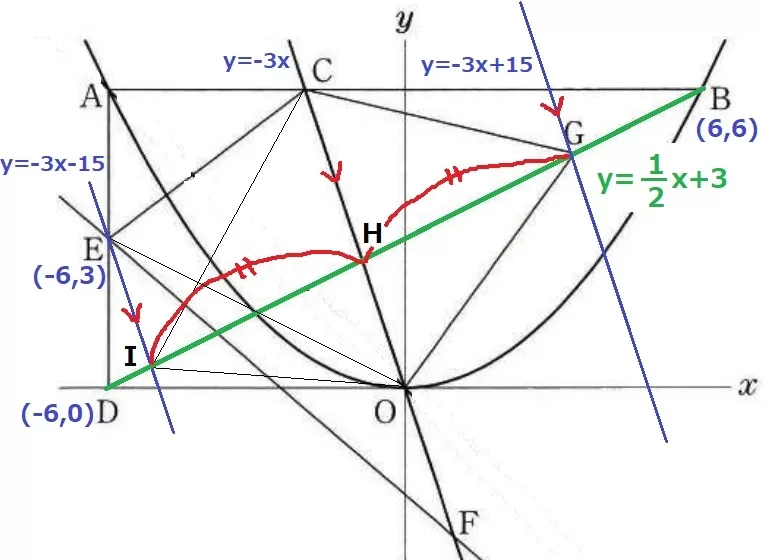
ＤＢ；ｙ＝１/２ｘ＋３
ＤＢとＣＦの交点をＨとする。
Ｅを通るＣＦに平行な線を引き、ＤＢとの交点をＩとする。
等積変形で△ＣＥＯ＝△ＣＩＯ
ｙ＝－３ｘ＋ｂにＥ（－６、３）を代入→ＥＩ；ｙ＝－３ｘ－15
△ＣＩＯ＝△ＣＯＧ→ＩＨ＝ＧＨ
Ｇを通るＣＦに平行な直線の式→ｙ＝－３ｘを対称の軸としてｙ＝－３ｘ－15を対称移動させた直線。
→ｙ＝－３ｘ＋15（ｙ＝－３ｘ－15の切片が＋15に変わる）
Ｇはｙ＝１/２ｘ＋３とｙ＝－３ｘ＋15の交点だから、
１/２ｘ＋３＝－３ｘ＋15
ｘ＝24/７
大問５（確率）
（ア） 49.5％
カード【４】だけを残す→カード５枚を取り除く。
操作２は結局１枚しか取り除かないので、操作１で４枚取り除く必要がある。
⇒約数が４個ある６を取る→ａ＝６が確定する。
ａ＝６のとき、残りは【４】【５】。
【４】だけを残すには４以外であればいい→ｂは５通り。
全体は６×６＝36通りで５通りしかないから、確率は５/36。
（イ） 48.0％
●約数を整理●
１→１
２→１・２
３→１・３
４→１・２・４
５→１・５
６→１・２・３・６
〔全体－６が取り除かれる＝６が残る〕余事象で攻める。
●ａ＝６
６は取り除かれたので、ｂは何でもいい。６通り
●ａ＝５
ｂは取り除かれた１・５、もしくは６を出す。３通り
●ｂ＝４
ｂは取り除かれた１・２・４、もしくは６を出す。
つまり、ｂは約数の個数＋１をすればいい。３＋１＝４通り
●ｂ＝３
２＋１＝３通り
●ｂ＝２
２＋１＝３通り
●ｂ＝１
１＋１＝２通り
６＋３＋４＋３＋３＋２＝21通り
６を含むのは36－21＝15通りだから、確率は15/36＝５/12
大問６（空間図形）
（ア） 51.3％
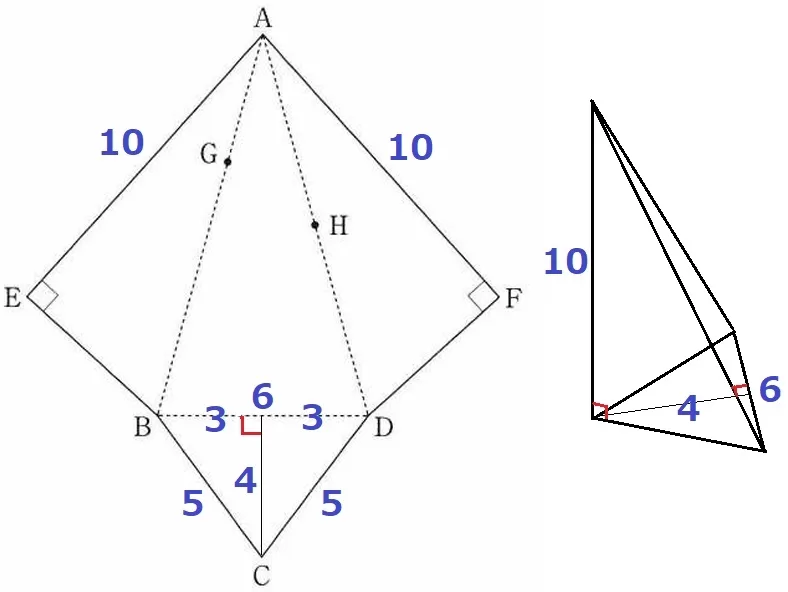
△ＢＣＤは直角二等辺ではないことに注意！
二等分すると３：４：５の直角三角形になる。
三角錐の体積は、６×４÷２×10÷３＝40ｃｍ3 【２】
（イ） 4.8％!!
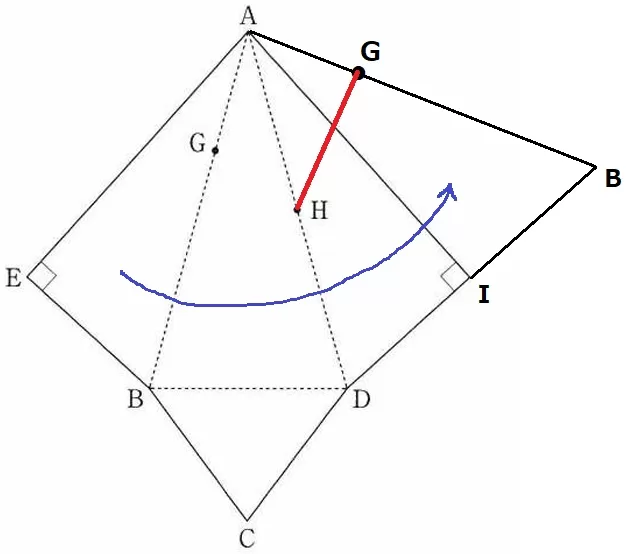
△ＡＥＢを右側に移す。
ＧＨを一直線で表すとこのようになる。
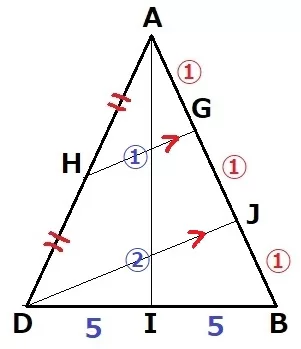
Ｄを通るＨＧに平行な線をひき、ＡＢとの交点をＪとする。
ＡＨ：ＨＤ＝ＡＧ：ＧＪ＝１：１
中点連結定理より、ＤＪ＝ＨＧ×２＝②
ＪはＧＢの中点である。
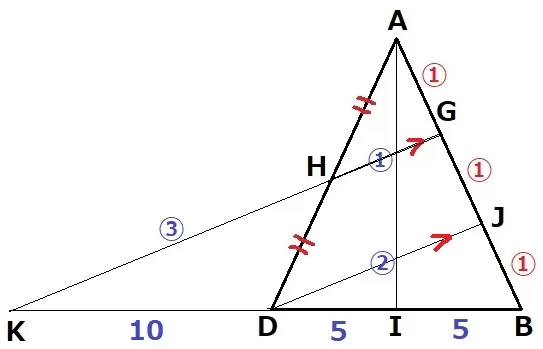
ＧＨとＢＤを延長、交点をＫとする。
ＧＪ：ＪＢ＝１：１より、ＫＤ＝ＤＢ＝10ｃｍ
中点連結定理より、ＫＧ＝ＤＪ×２＝④
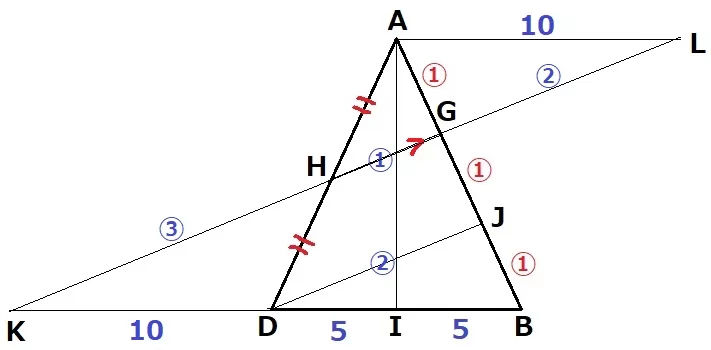
ＫＧを延長、Ａから真横に引いた線との交点をＬとする。
△ＫＤＨ∽△ＬＡＨより、ＡＬ＝10ｃｍ
△ＫＢＧ∽△ＬＡＧより、ＬＧ＝ＫＧ÷２＝②
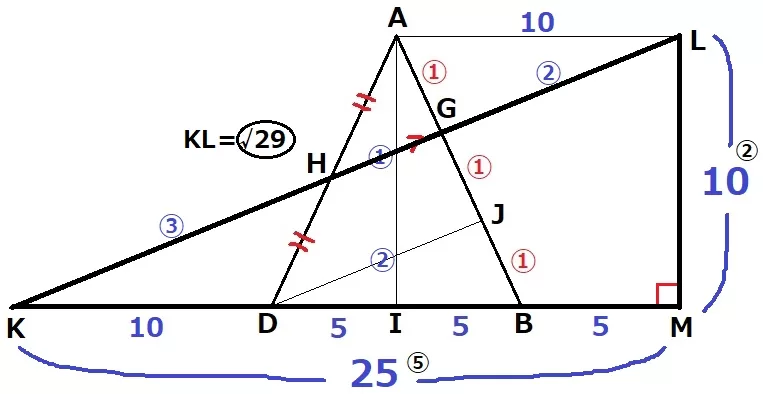
ＫＢを延長、Ｌからの垂線の足をＭとする。
ＬＭ＝10ｃｍ、ＫＭ＝25ｃｍ
辺の比はＬＭ：ＫＭ＝10：25＝②：⑤
△ＬＫＭで三平方→ＬＫ＝〇√29＝10×〇√29/②＝５√29ｃｍ
ＧＨ＝５√29×①/⑥＝５√29/６ｃｍ
昨年並みの難易度であった。８割を超えるには幾何の攻略を要する。
大問１
例年通り。15点とろう。
大問２
（ア）神奈川は係数が互いに素なのが多い印象。
（ウ）初手はｙ変域からグラフが上向きなのか、下向きなのかを判断する。
大問３
（ア）ⅰ：誘導に従って正解したい。
ⅱ：迷子になりやすい。ⅰの等角を使う。
外側にある73°をどう巻き込むか。
決め手は弧ＣＦの円周角、∠ＣＡＦ＝∠ＣＤＦ
（イ）ⅰ：ABとＣで人数が異なる。
不幸にも最小値と最大値がどれも同じ階級…Ｑ１～Ｑ３が何番目の値かを調べておく。
Ｃ中＝Ｙと決めたら、ＸとＺは何が違うのか。Ｑ２よりＱ１が判断しやすい。
ⅱ：25分を仮の平均として、ヒストグラムの形から判断する。
左右対称であれば真ん中が平均値になる。
（ウ）意表を突いた構図で、ちょっと考えてダメだったら後回し。
12ｃｍが多く、ＥＣ＝12が浮いている。他にも12ｃｍはないか。
直角三角形の中点Ｄを中心とする円を描けるかがポイントであった。
角度調査→∠ＡＤＥ＝45°、ＧＨはどんな線分かを分析する。
（エ）中受では食塩水の濃度操作は頻出分野だが、高受はめずらしい。
減ったａｇは４％、増えたａｇは100％。
大問４
（ウ）面積比３：２、底辺の比が３：２から、高さが１：１だと見やすい。
傾き－３の３本の直線で、真ん中のｙ＝－３ｘは原点Ｏを通過する。
ということは、左右の直線の切片は絶対値が同じ。
大問５
（１）個別で調べるのではなく、方針を立てたい。
５枚取り除くにはどうするか？操作２では分岐があるが１枚しか取らない。
以上から、操作１で出すべき出目が決まる。
（２）操作２では最大値６が取られやすい。
余事象を使うと、ｂは約数の個数＋１で整理ができる。
大問６
（イ）ＧＨを作図する。
斜線なので、どこかで三平方を使う。ＡＩ⊥ＤＢからＡＩ＝10ｃｍを利用する。
数値が汚いので計算力で乗り切るか、整数値の辺→辺の比を使って処理を簡略化する。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
初コメ失礼します。
大問３(ア)iiですが、別解を思いついたので書かせていただきます。(誘導は生かせてないですが)
∠ABC=∠ACB(仮定)、∠ACB=∠ADB(弧AB)から∠ABE=∠ADBで、∠BAE=∠DABが共通なので△BAE∽△DAB
よって、求める角∠AEBは∠ABDと等しい。
円に内接する四角形の性質から、∠ABDは∠ICDと等しい。
∠CAF=∠CDF(弧CF)、∠AIF=∠DIC(共通)より△AIF∽△DICだから、∠ICDは∠IFAと等しい。
四角形CIFHの内角の和で、73+(180-61)+2∠ICD=360、これを解いて∠ICD=∠84°より∠AEB=84°
いい別解なのかは分かりませんが、個人的には計算量が減るのでこっちの方が楽だと思います。
コメントありがとうございます。
図形の特徴を紐解いた面白い解法で素晴らしいです！
図形の右側に情報が寄っているので、サボは∠ＡＢＤに注意を払わなかったです。
せっかくですし、匿名さんがよろしければ記事に別解として掲載したいのですが大丈夫でしょうか？
可能であれば掲載するハンドルネームかリンク先等があれば教えてください。
サボ
ありがとうございます。掲載していただいて大丈夫です。
ハンドルネームはこれでお願いします。
こちらこそありがとうございます。
掲載させていただきました。ご査収くださいませ。
また何かございましたら、気兼ねなくコメントしてください。
サボ
今年結構簡単でしたね。大問3の(ウ)もムズそうに見えて、15度、75度、90度の辺の比を覚えていれば秒で解けるし。知っているかどうかで解く時間が大きく変わってしまう問題はやめてほしいですね。
コメントありがとうございます。
その辺の比は中学数学では許容範囲かなと(;^ω^)消された線分を適切に付け足すところが面白いと思いました。
神奈川は３月中に検査結果を公表しますので、正答率がどうなのかちょっと楽しみです。