平均33.5点（前年比；＋4.6点）
問題はコチラ→ＰＤＦファイル
大問１（計算）
（１）
－７＋５＝－２
（２）
６÷（－２/３）
＝６×（－３/２）＝－９
（３）
１－0.39＝0.61
（４）
√２＋√18
＝√２＋３√２＝４√２
（５）
４ａ×（－３ａ）2
＝４ａ×９ａ2＝36ａ3
（６）
３（２ｘ＋ｙ）－２（ｘ－ｙ）
＝６ｘ＋３ｙ－２ｘ＋２ｙ
＝４ｘ＋５ｙ
大問２（小問集合）
（１）
３ｘ－５＝ｘ＋３
２ｘ＝８
ｘ＝４
（２）
２ｘ＋ｙ＝11 …①
ｘ＋３ｙ＝３ …②
６ｘ＋３ｙ＝33 …①×３
－) ｘ＋３ｙ＝３ …②
５ｘ ＝30
ｘ＝６
②に代入。
６＋３ｙ＝３
ｙ＝－１
ｘ＝６、ｙ＝－１
（３）
（ｘ－６）（ｘ＋３）
＝ｘ2－３ｘ－18
（４）
ｘ2－36＝（ｘ＋６）（ｘ－６）
（５）
ｘ2＋５ｘ－１＝０
因数分解ができないので解の公式を適用。
ｘ＝（－５±√29）/２
（６）
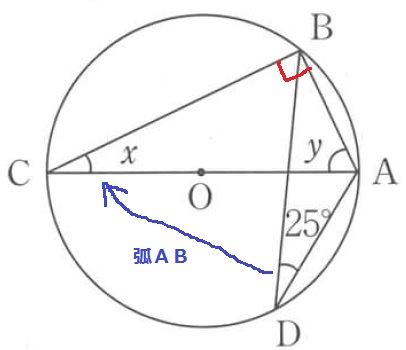
弧ＡＢの円周角より、∠ＡＣＢ＝∠ＡＤＢ
ｘ＝25°
半円の弧に対する円周角は直角→∠ＡＢＣ＝90°
△ＡＢＣの内角より、ｙ＝180－（25＋90）＝65°
（７）
４月の観光客数を【100】とすると５月は【105】
8400×100/105＝8000人
（８）
ありがたいことにデータが昇順に並んでいる。
平均値…（２＋４＋６＋７＋８＋８＋９＋９＋10）÷９＝63÷９＝７点
中央値（メジアン）…９人の中央値は５番目の値で８点
（９）
標本調査を行うのが適当な調査を選ぶ。
全部を調べるのが全数調査、一部の標本を調べて全体（母集団）を推定するのが標本調査。
ア：製造されたすべての蛍光灯の寿命を調査するのは困難。
工業製品は品質がほぼ均一なので、無作為に抽出した一部を調査すれば足りる。
イ：健康状態は１人１人異なるから、全員を検査しなければ意味がない。
ウ：世論調査は世間の人々がどう考えているか、その動向を調査するもの。
おおよその傾向がわかれば良いので標本調査で足りる。
総務省統計局が実施する国勢調査は国の基本となるデータを収集するので全数調査。
エ：野生動物をすべて調査するのは困難なので標本調査を行う。
標識再捕獲法といい、無作為に捕獲した個体に標識（しるし）をつけ、
再度、無作為に捕獲して標識のついた個体数から母集団を推定する。
ア・ウ・エ（完全解答）
＠テレビの視聴率＠
標本（サンプル）の大きさはどの程度求められるか。
大学レベルの統計学の知識が必要だと思うのでサボにはわかりませんが、
テレビの視聴率を計測する機器が設置されている台数の割合は、全体の0.01％もないそうです。
視聴率調査に協力している人を全く見掛けない理由（ねとらぼ）
↑この記事によると、2017年10月時点で調査対象世帯は全体の0.00005％以下となっている…。
それだけで残りの99.999…％以上を推し量って良いものなのか疑問に思われますが、
統計学的には十分信頼するに足りるサンプル数なんだとか。
どうやら母集団が大きくなるほど、標本の大きさは思ったより小さくても間に合うようです。
反対に母集団が小さいと（例えば１クラス内の動向とか）多くの標本をとらないといけない。
大問３（確率）
（１）
１枚目を戻さずに２枚目を取る。
５×４＝20通り
（２）
偶数になるには、一の位が２か４であればいい。
一の位は２通り。十の位はそれ以外で４通り。
偶数のケース…２×４＝８通り
前問より全体で20通りだから、確率は８/20＝２/５
（３）
偶数は一の位が２通りしかないが、奇数は３通りある。
ということは、奇数の方が作りやすい。
ア
*整数は偶数か奇数しかないので、奇数の確率は１－２/５＝３/５
大問４（作図）
（１）
作図問題。
線対称でＡに対応するＰを作図する。
わかりやすいのは左。
Ａを通るℓの垂線を引く。対応するＰはこの線上にある。
ℓとの交点をＯする。対応する辺は等しいのでＡＯ＝ＰＯ
Ｏに針を合わせ、Ａの逆側の点がＰとなる。
別解１は、まずＡに針を合わせて弧を描き、ℓとの交点をＱ、Ｒとする。
次にＡＱ（ＡＲ）の長さを維持したまま、ＱＲの垂直二等分線のやり方で反対側の点がＰとなる。
四角形ＡＱＰＲは４辺が等しい正方形。対角線ＱＲを対称の軸として左右対称。
別解２はℓ上の点Ｓを中心に、Ａを通る弧（円）を作成。
Ａに鉛筆を合わせたまま針を上に持っていき、ＡＳと長さが等しいℓ上の点Ｔを中心に円をつくる。
反対側で交わった点がＰとなる。
（２）
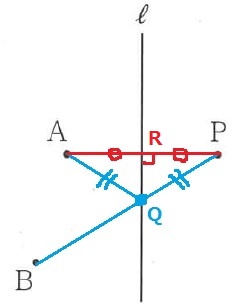
ＡＱ＋ＱＢが最短距離となるＱの位置は、線分ＢＰと直線ℓとの交点である。
すなわち、ＡＱ＋ＱＢ＝ＢＰ
ＡＰと直線ℓとの交点をＲとすると、△ＡＱＲと△ＰＱＲは線対称から、
ＡＲ＝ＰＲ、共通辺ＱＲ、直角より２辺とあいだの角が等しい合同図形。
ＡＱ＝ＰＱとなり、ＡＱ＋ＱＢ＝ＢＰが導ける。
イ
大問５（整数）
（１）
実際にカレンダーに囲ってみよう。
ａ＝４
（２）
ｂ＝ａ＋７、ｃ＝ａ＋８、ｄ＝ａ＋９
ｅ＝ｄ＋７＝（ａ＋９）＋７＝ａ＋16
ａ＋ｂ＋ｃ＋ｄ＋ｅ
＝ａ＋（ａ＋７）＋（ａ＋８）＋（ａ＋９）＋（ａ＋16）
＝５ａ＋40＝５（ａ＋８）
ａ＋８が自然数だから、５（ａ＋８）は５の倍数。
したがって、ａ＋ｂ＋ｃ＋ｄ＋ｅは５の倍数。
①７②８③９④16⑤８（完全解答）
（３）
実際に具体的な数値を入れて確かめればいいが、
沖縄は大問が10個もあるので時間がない。
ポイントは対称性。
中央の値ｃにすべてを集めると、平均の要領で均すことができる。
たとえば、ｂ・ｃ・ｄは連続する３つの整数だから、
３・４・５の場合は３＋５＝４×２と、真ん中の倍数に変形して４で均せる。
同様に、ａ・ｃ・ｅもａ・ｂ・ｃ・ｄ・ｅも中央をｃとして対称性があるが、
ウのａ・ｂ・ｃ・ｄの並びには対称性がない。
よって、ウ。
大問６（数量変化）
（１）
迷ったら図示してみよう。
底辺ＡＰ＝４ｃｍ、高さＢＣ＝８ｃｍ
ｙ＝４×８÷２＝16
（２）
底辺ＡＰ＝ｘｃｍ、高さＢＣ＝８ｃｍ
ｙ＝ｘ×８÷２＝４ｘ
（３）
△ＡＰＣの面積の変化をとらえる。
ＡがＢに到着する12秒後までは増えるが、それを境に減少し、Ｃに着くと０ｃｍ2になる。
イ
（４）
ＰがＢにつく12秒後の前後で２通りある。
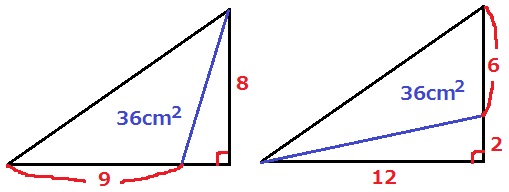
36×２÷８＝９ｃｍ
36×２÷12＝６ｃｍ、Ｐが動いた距離は12＋（８－６）＝14ｃｍ
Ｐは毎秒１ｃｍ動くので９秒後と14秒後。
＠別解＠
高校受験の正攻法は方程式を立てる。
０≦ｘ≦12のとき、（２）よりｙ＝４ｘ
ｙ＝36を代入してｘ＝９→９秒後
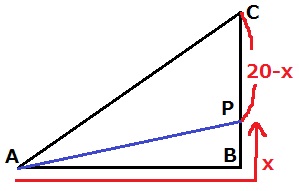
12≦ｘ≦20のとき、Ｐはｘ秒後にｘｃｍ動くから、ＰＣ＝20－ｘｃｍ
ｙ＝（20－ｘ）×12÷２＝－６ｘ＋120
ｙ＝36を代入してｘ＝14→14秒後
大問７（関数）
（１）
ｙ＝４/ｘにｘ＝－４を放り込む。
ｙ＝－１
（２）
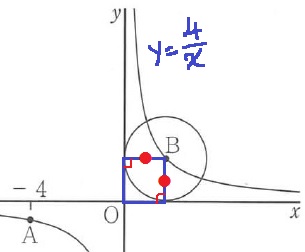
円の半径から●の部分が等しい。（青い四角形は正方形）
反比例はｘ座標とｙ座標の積が一定→●×●＝４
●＞０で●＝２
Ｂ（２、２）
（３）
Ａ（－４、－１）→Ｂ（２、２）
右に６、上に３なので、傾きは３/６＝１/２
Ｂから左に２、下に１移動して、切片は１。
ｙ＝１/２ｘ＋１
（４）
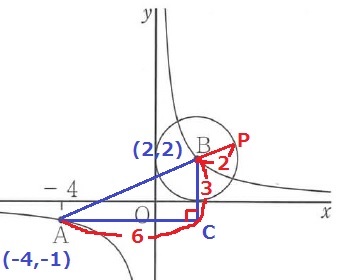
ＰはＡＢの延長線と円との交点。
半径からＢＰ＝２ｃｍ
直角三角形ＡＢＣで三平方→ＡＢ＝３√５ｃｍ
ＡＰ＝３√５＋２ｃｍ
大問８（平面図形）
（１）
△ＡＯＥ≡△ＣＯＦの証明。誘導に従って空欄を補充する。
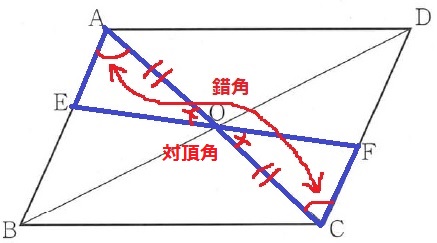
平行四辺形の対角線は各々の中点で交わる→ＡＯ＝ＣＯ
ＡＥ//ＤＣの平行線→錯角で∠ＯＡＥ＝∠ＯＣＦ
対頂角で∠ＡＯＥ＝∠ＣＯＦ
１組と両端角が等しいから合同。
【錯角は等しい】
【対頂角は等しいから∠ＡＯＥ＝∠ＣＯＦ】
【１組の辺とその両端角が等しい】
（２）
Ｏを挟んでＥの反対側がＦで、前問の△ＡＯＥ≡△ＣＯＦは維持される。（ア〇）
となると、対応する角が等しいので∠ＡＥＯ＝∠ＣＦＯ（イ〇）
対応する辺も等しくＯＥ＝ＯＦ（ウ〇）
よって、誤りはエ。ＯＥの長さは変動する。
（３）
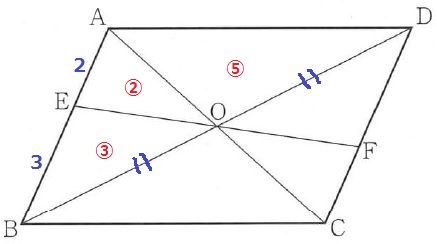
△ＡＯＥ：△ＥＯＢ＝ＡＥ：ＥＢ＝②：③
平行四辺形の対角線はおのおのの中点で交わる→ＢＯ＝ＤＯ
△ＡＤＯ＝△ＡＯＢ＝⑤
△ＡＯＥ：△ＡＢＤ＝②：⑩＝１：５
大問９（空間図形）
（１）
側面の扇形の弧＝底面の円の円周
√３×２×π＝２√３πｃｍ
（２）
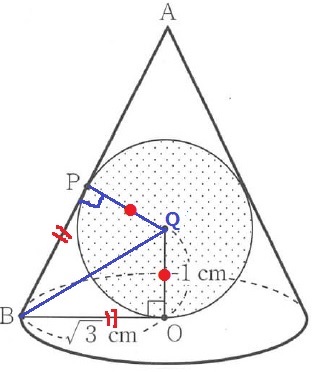
断面で考える。
【円外の１点からひいた２本の接線の長さは等しい】
ＢＰ＝ＢＯ＝√３ｃｍ
*なぜそうなるのか。
球（円）の中心をＱとすると、△ＢＯＱと△ＢＰＱにおいて、
半径でＱＯ＝ＱＰ、半径と接線は垂直で∠ＱＯＢ＝∠ＱＰＢ＝90°
共通辺ＢＱより、斜辺と他の１辺が等しい直角三角形で合同。
対応する辺からＢＰ＝ＢＯとなる。
（３）
差が開きやすい。
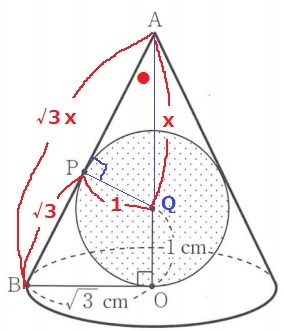
△ＡＰＱと△ＡＯＢは２角が等しく∽
ＡＱ：ＡＢ＝ＰＱ：ＯＢ＝１：√３
ＡＱ＝ｘｃｍとおくと、ＡＰ＝√３ｘｃｍ
△ＡＢＯで三平方。
（√３ｘ）2＝（ｘ＋１）2＋（√３）2
３ｘ2＝ｘ2＋２ｘ＋１＋３
２ｘ2－２ｘ－４＝０ ←両辺を÷２
ｘ2－ｘ－２＝（ｘ＋１）（ｘ－２）＝０
ｘ＞０ゆえ、ｘ＝２
ＡＱ＝２ｃｍ
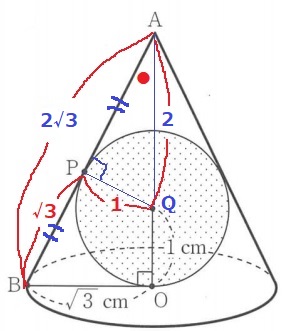
ＡＢ＝２√３ｃｍとなり、ＰはＡＢの中点である。
体積比は辺の比の３乗だから、円錐：円錐台＝２3：２3－１3＝８：７
求積すべき円錐台の体積は円錐の体積の７/８倍となる。
√３×√３×π×３÷３×７/８＝21π/８ｃｍ3
大問10（文章題）
（１）
ルールの確認。
Ｐ：表示（そのまま）、Ｑ：＋５、Ｒ：÷３した余り
Ｑ：１＋５＝６
Ｑ：６＋５＝11
Ｒ：11÷３＝３…２→２
Ｐ：２（表示）
（２）
Ｑは増える、Ｒは減る。
１から０に減らすには、Ｒで０にする。
Ｒの前は３の倍数になるまでＱで増やす。
Ｑ：１＋５＝６
Ｒ：６÷２＝３→０
Ｐ：０（表示）
Ｑ：０＋５＝５
Ｑ：５＋５＝10
Ｒ：10÷３＝３…１→１
Ｐ：１（表示）
以上の命令で０と１が繰り返し表示される。
ＱＲＱＱＲ
（３）
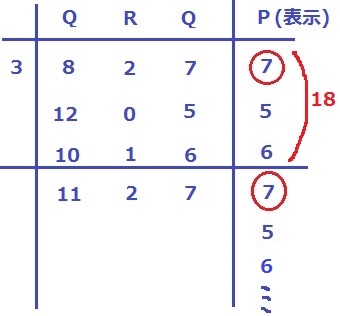
実際にやってみる。
留意点は最初の３は含まないこと。カウントすべきはＰで表示された数だけ。
すると、表示される数は〔７・５・６〕を１ループとする繰り返しが見つかる。
１ループの和は７＋５＋６＝18
32÷３＝10ループ…２個
18×10＋７＋５＝192
（４）
ラストに推論要素を含む設問が登場した。
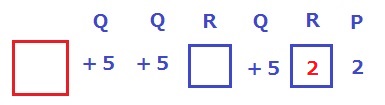
情報整理。
最後は２だから直前のＲは２。
手前にさかのぼっていく。
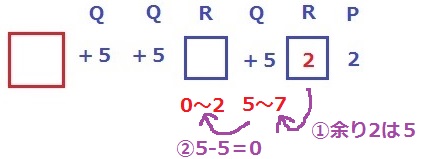
Ｒは３で割ったときの余りだから０～２の範囲。
Ｑで＋５されて５～７の範囲。
２番目のＲが２なので、５～７のなかで３で割って余りが２なのは５しかない。
手前のＱは５となる。
１番目のＲは５－５＝０
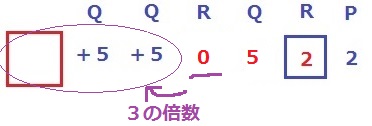
１番目のＲは０→□＋５＋５が３の倍数
□＝２を入れると、12は３で割り切れるので条件に適合。
２に３を足した５、さらに３を足した８も条件に適合する。
２、５、８（完全解答）
時間との勝負なので、簡単な問いでつまづかないこと！
大問１
全問死守。（３）は小学生でも解ける。
大問２
ここも全問正解を狙いたいが、他県で（７）の類題は正答率が良くなかった。
（９）４つ中３つ選ぶので、少し勇気がいる。
大問５
カレンダー問題は頻出。
（３）真ん中がちょうど平均になる。この発想で秒殺できる。
大問６
（４）実際に２パターンの三角形をつくり、底辺や高さを出したほうが早い。
大問８
標準レベル。複雑な図形ではない。
大問９
（３）∽が見えるかどうか。
前半でモタモタしているとここらへんで体力が切れそう。
大問10
条件をサッと理解しないとタイムアップ。
高得点をとるには取捨選択も決め手になる。
公立高校入試解説ページに戻る
コメント
沖縄県で塾講師のバイトをしている大学生です。
サボさんの解答は非常にスッキリしていて、自分自身の解答作成の参考にさせてもらっています。
特に何が出来るという訳では無いのですが、これからもサボさんのブログで勉強させて頂きます！
コメントありがとうございます(*’ω’*)
お役に立てて何よりです(^^ゞ
私は理数系の人間ではないので不安もあるのですが、とても励みになります。
いろいろアップする予定ですので、また遊びにきてくださいませ^^