2023年度　三重県公立高校入試問題・前期過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
（－６）²＋24÷（－３）
＝36－８
＝28

（２）
４（２ｘ－１）－６ｘ
＝８ｘ－４－６ｘ
＝２ｘ－４

（３）
30ａｂ÷６/５ｂ
＝25ａ

（４）
√18－４/√８
＝３√２－４/(２√２)
＝３√２－√２
＝２√２

（５）
（ｘ－６）（ｘ＋３）＝３（ｘ－９）
ｘ²－３ｘ－18＝３ｘ－27
ｘ²－６ｘ＋９
＝（ｘ－３）²＝０
ｘ＝３

（６）
全体のミカンはｘ個。
配る予定のミカンは５ｙ個。
ミカンが不足したということは、５ｙの方が大きかった。
ｘ＜５ｙ

（７）
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加したときの変化の割合はａ（ｐ＋ｑ）
（２＋６）ａ＝４
ａ＝１/２

（８）
【球の表面積Ｓ＝４πｒ²】
４×π×５²＝100πｃｍ²

（９）

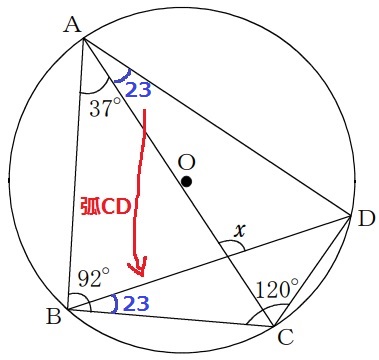
円に内接する四角形の対角の和は180°→∠ＢＡＤ＋∠ＢＣＤ＝180°
∠ＣＡＤ＝180－（120＋37）＝23°
弧ＣＤの円周角より、∠ＤＢＣ＝23°

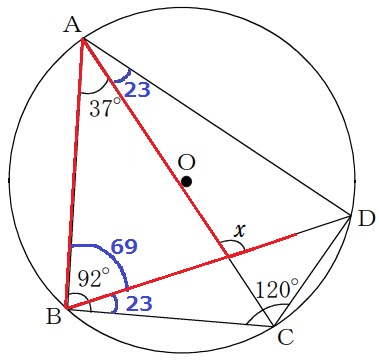
∠ＡＢＤ＝92－23＝69°
最後に赤線で外角定理を適用→ｘ＝37＋69＝106°

（10）

①線分ＯＸとＯＹから等距離→∠ＸＯＹの二等分線
②∠ＯＰＡ＝90°→①の二等分線とＡを通る垂線の交点がＰ。
公式解答の例２では、半円の弧に対する円周角から∠ＯＰＡ＝90°を導いている。

大問２（データの活用）

（１）
35人の中央値は、（35＋１）÷２＝18番目
これは20分以上30分未満の階級に含まれる。
たろうの30分は30分以上40未満の階級に含まれるから、遅いグループのＢ。
①…20、②…30、③…Ｂ

（２）
１年生の30～40分の階級の相対度数は、７/35＝１/５
２年生の30～40分の階級（ア）を①とおくと、合計の（イ）は⑤にあたる。
残りの階級の和の４＋８＋10＋２＋０＝24人が④なので、
ア…24×①/④＝６人
イ…24＋６＝30人
ア…６、イ…30

大問３（確率）

（１）
平面ＡＢＣＤ上に線分ができる→Ｂ・Ｃ・Ｄのどれかを取ればいい。
７枚中３枚だから、確率は３/７。

（２）

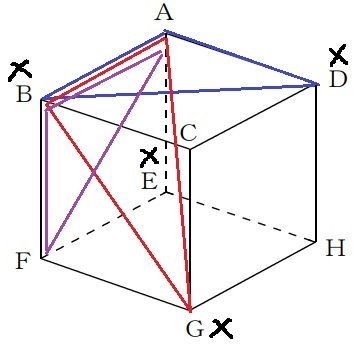
正三角形はどこで現れるか。
試しにＡＢで調べてみると正三角形を作れない。
Ｂがダメなら、同じくＡと隣接しているＤ・Ｅもダメ！
ＡＧは直方体の対角線で、同じく正三角形が作れない。

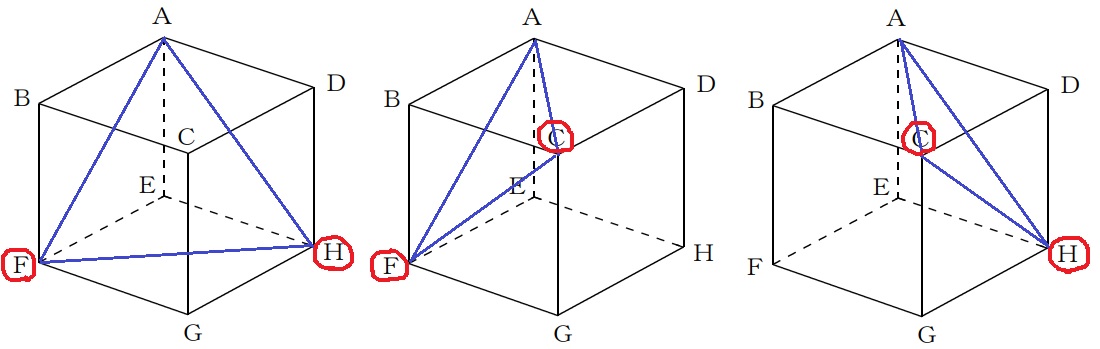
正方形の対角線を１辺とする、この３つしかない。
すなわち、Ｃ・Ｆ・Ｈから２つ選べばいい。
₃Ｃ₂＝３通り
７つから２つを選ぶ組み合わせは、₇Ｃ₂＝21通り
確率は、３/21＝１/７

大問４（平面図形）

（１）
△ＥＡＦ≡△ＣＧＨの証明。

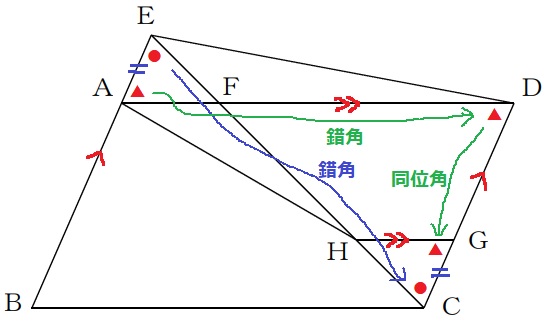
仮定より、ＥＡ＝ＣＧ
ＢＥ//ＣＤより、錯角で∠ＡＥＦ＝∠ＧＣＨ（●）
同じく錯角で、∠ＥＡＦ＝∠ＦＤＧ（▲）
ＡＤ//ＨＧの同位角で、∠ＣＧＨ＝（▲）
１辺と両端角が等しいので合同。

（２）

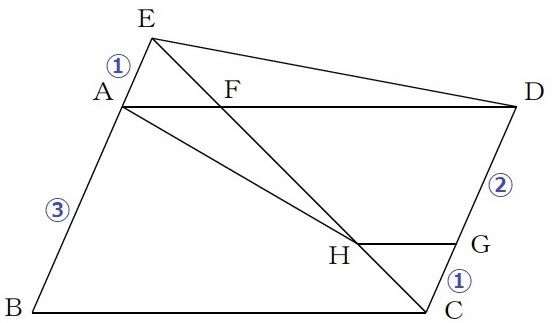
ＡＥ＝①とすると、ＡＢ＝③
前問の合同から、ＧＣ＝ＡＥ＝①
平行四辺形の対辺は等しいので、ＤＣ＝③
ＤＧ＝③－①＝②

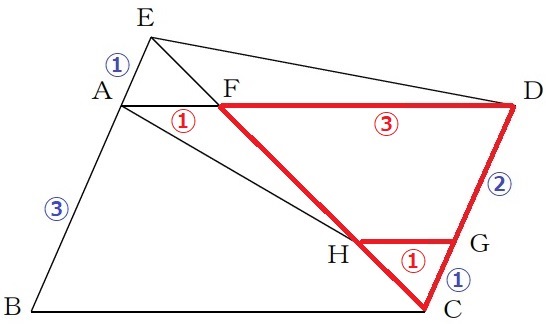
ＨＧ＝①とする。
△ＣＧＨ∽△ＣＤＦより、相似比は①：③だからＦＤ＝③
また、合同からＦＡ＝ＨＧ＝①
ＡＤ＝ａ＝④なので、ＨＧ＝ａ×①/④＝１/４ａｃｍ

（３）

面積が最も小さい△ＥＡＦの面積を【１】とする。
ＡＦ：ＦＤ＝①：③から、△ＥＦＤ＝【３】
合同で△ＣＧＨ＝【１】
面積比は相似比の２乗。
△ＣＧＨ：△ＣＤＦ＝【１】：【９】→四角形ＦＨＧＤ＝【８】

ＦＤ//ＨＧから、ＦＨ：ＨＣ＝ＤＧ：ＧＣ＝２：１
合同の対応する辺から、ＥＦ＝ＣＨ＝１
ＥＦ：ＦＨ＝１：２より、△ＡＨＦ＝【２】
したがって、△ＥＦＤ：四角形ＡＨＧＤ＝３：10

大問５（空間図形）

（１）
４×４÷２×６＝48ｃｍ³

（２）

立面図は正面、平面図は真上から見た図。
正四角柱と円柱はＯＫ。

正三角柱は底面が正三角形なので平面図が×。
正五角柱にいたっては立面図も平面図も×。
正しく描くと上図のようになる。
イ・エ

＠余談＠

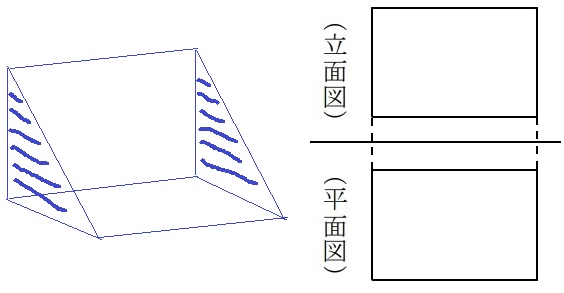
三角柱でも底面が直角三角形（か鈍角三角形）であれば条件を満たす。

大問６（数量変化）

（１）
パンフレット１部をｘｇ、箱をｙｇとする。
14ｘ＋ｙ＝275　…①
31ｘ＋ｙ＝530　…②
②－①で、17ｘ＝255
ｘ＝15
①に代入してｙ＝65
パンフレット１部…15ｇ、箱…65ｇ

（２）①
４×30＋16＝136ｇ
グラフの横軸の１目盛りは50ｇ。
136ｇは210円。

②
封筒２枚のとき、全体の重さは４×140＋16×２＝592ｇ

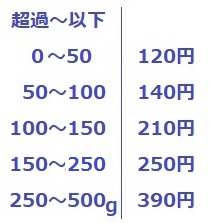
重さと料金を表でまとめるとこうなる。
592ｇを２つに分けて、料金を安く抑えたい。

２枚の封筒を平均すると、592÷２＝296ｇ
→必ず１枚は296ｇ以上になってしまう。（390円の支払いは確定）
１枚を500ｇに偏らせると、他方は592－500＝92ｇ（140円）
料金は、140＋390＝530円

大問７（関数）

（１）①
ｙ＝－２ｘ－２にｘ＝－２を代入。
Ｐ（－２、２）
これをｙ＝１/２ｘ＋ｂに代入。
２＝１/２×（－２）＋ｂ
ｂ＝３

②
Ｒはｙ＝１/２ｘ＋３とｙ＝ｘ－２の交点である。
１/２ｘ＋３＝ｘ－２
１/２ｘ＝５
ｘ＝10
ｙ＝ｘ－２にｘ＝10を放り込んで、ｙ＝８
Ｒ（10、８）

③

ＰＲの中点をＴとする。
ＰＴ：ＴＲ＝１：１から、△ＰＱＴは△ＰＱＲの半分である。
Ｔのｘ座標は、ＰとＲのｘ座標の平均→（－２＋10）÷２＝４

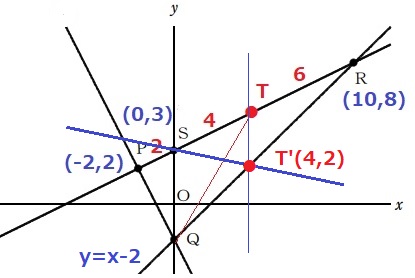
△ＰＱＴ＝△ＰＱＳ＋△ＳＱＴ
Ｔを通るｙ軸に平行な線をひき、ＱＲとの交点をＴ’とする。
等積変形で△ＳＱＴ＝△ＳＱＴ’だから、四角形ＰＱＴ’Ｓは△ＰＱＴと等積。
四角形ＰＱＴ’Ｓは△ＰＱＲの半分で、ＳＴ’が△ＰＱＲを２等分する。

ｙ＝ｘ－２にｘ＝４を代入して、Ｔ’のｙ座標は２。
Ｓ（０、３）→Ｔ’（４、２）
右に４、下に１だから傾きは－１/４。切片はＳのｙ座標の３。
ｙ＝－１/４ｘ＋３

（２）

切片ｂを操作する。
→ｙ＝１/２ｘを上下に平行移動させて△ＳＱＲ＝11ｃｍ²となるタイミングを探す。

ＳＯの長さがｂにあたる。
ＳＯはＳＱ上にある線分で、ＳＱがわかればＯＱ＝２ｃｍだからＳＯもわかる。
△ＳＱＲと相似な図形をつくってＳＱを求めてみる。

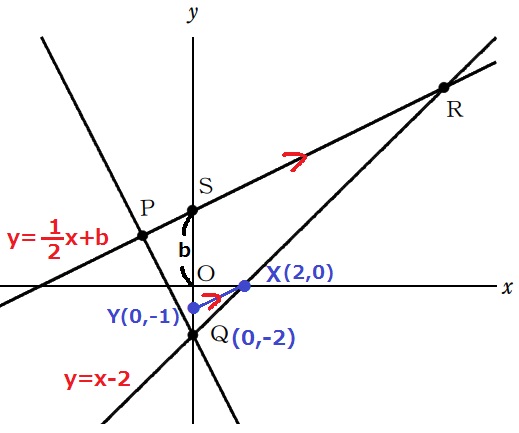
ｙ＝ｘ－２とｘ軸との交点をＸとする。Ｘ（２、０）
Ｘを通るＳＲに平行な線をひき、ｙ軸との交点をＹとする。
この直線の傾きは１/２なので、Ｘから左に２、下に１進んだところがＹ。
Ｙ（０、－１）

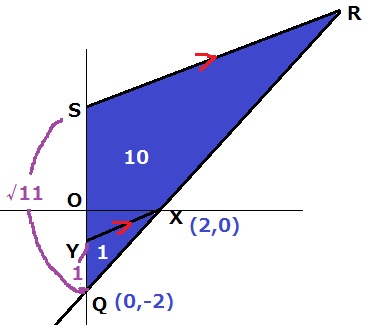
△ＹＱＸの面積は、１×２÷２＝１ｃｍ²
△ＳＱＲ∽△ＹＱＸの面積比は11：１→相似比は√11：１。
ＹＱ＝１ｃｍなので、ＳＱ＝√11ｃｍ
ｂ＝ＳＱ－ＯＱ＝√11－２（－２＋√11）