問題PDF
さまざまな形をしたマス目に、以下のルールにしたがって、整数を書きます。
・1からマス目の数までの整数を、各マスに1つずつ書く。
・どの行を横に見ても、右のマスほど数が大きくなっている。
・どの列を縦に見ても、下のマスほど数が大きくなっている。
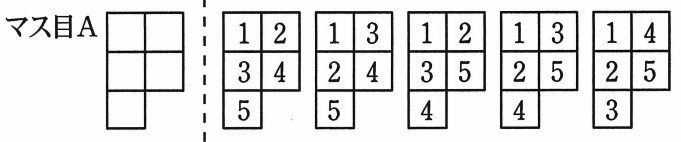
例えば、上のようなマス目Aは、5個のマスからなるマス目なので、1から5までの整数を書きます。
このとき、整数の書き方は5通りです。
次のマス目B、C、Dに整数を書くとき、その書き方はそれぞれ何通りですか。
なお、下のマス目に書きこんで考えてもかまいません。



@解説@
甲陽学院の入試問題は大問6まであります。1個ずつ調べあげるのはNG!
(1)
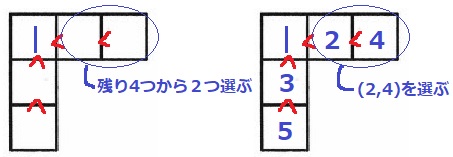
最小値1の場所が確定する。1の右2マスを考える。
残りの4つから2つの数を選ぶと、すべての数字の位置が確定する。
たとえば、(2、4)を埋めると上図のように1通りに決まる。
4C2=6通り
(2)

この手のタイプの問題は最小値か最大値で攻める。
最大値6は不等号の閉じた場所には置けない→上の3通りが考えられる。

6が右上にある場合、残りの5マスに注目すると問題文のマス目Aと同じである。
6が左下にある場合も同様だから、5×2=10通り
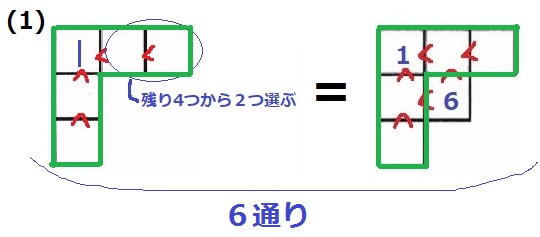
もう1つのパターンも残りの5マスに注目すると(1)と同じ→6通り
よって、10+6=16通り
(3)
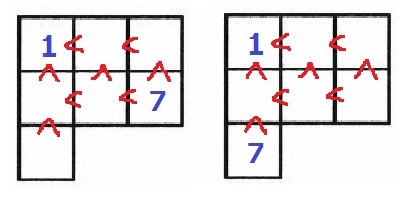
ここも最大数7の配置から考える。
不等号が開いている場所は上の2ヶ所。

残り6マスに注目すると(2)の16通りと同じ。

もう1つのパターンでは6の位置を確定する。
残りの5マスに注目するとマス目Aと同じ!
よって、16+5=21通り



コメント