合格者平均11.7点（前年比；－0.8点）
問題はコチラ→ＰＤＦファイル
2022年度、愛知Ｂ問題（数学）の解説はコチラ。
大問１（小問集合）
（１）
８＋（－３）×２
＝８－６
＝２
（２）
（２ｘ－３）/６－（３ｘ－２）/９
＝｛３（２ｘ－３）－２（３ｘ－２）｝/18
＝（６ｘ－９－６ｘ＋４）/18
＝－５/18
（３）
５ｘ2÷（－４ｘｙ）2×32ｘｙ2
＝５ｘ2÷16ｘ2ｙ2×32ｙ2
＝10ｘ
（４）
（√５－√３）（√20＋√12）
＝√100＋√60－√60－√36
＝10－６
＝４
（５）
５（２－ｘ）＝（ｘ－４）（ｘ＋２）
10－５ｘ＝ｘ2－２ｘ－８
ｘ2＋３ｘ－18
＝（ｘ＋６）（ｘ－３）＝０
ｘ＝－６、３
（６）
反比例はｘとｙの積が比例定数ａで一定。
ア：ｙ＝ｘ3
イ：ｙ＝35/ｘ
ウ：ｙ＝４ｘ
エ：ｙ＝15/ｘ
反比例はイ・エ。
（７）
平均値は、（１＋３＋５＋ａ＋10＋12）÷６＝（31＋ａ）/６
６個の中央値は３番目と４番目の平均だから（５＋ａ）/２。
これらを等式で結ぶ。
（31＋ａ）/６＝（５＋ａ）/２ ←両辺を６倍
31＋ａ＝３（５＋ａ）
ａ＝８
（８）
Ａ（－３、９）⇒Ｂ（６、36）
右に９、上に27だから、傾きは27/９＝３
原点を通るので、ｙ＝３ｘ
（９）
底面の円の半径の比がＰ：Ｑ＝３：５
底面積の比は、Ｐ：Ｑ＝９：25
ＰとＱは体積が等しいから、高さの比は底面積の逆比でＰ：Ｑ＝25：９
Ｑの高さはＰの９/25倍。
（10）
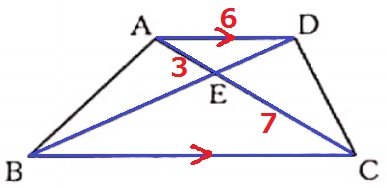
△ＡＤＥ∽△ＣＢＥより、ＢＣ＝６×７/３＝14ｃｍ
大問２（小問集合２）
（１）
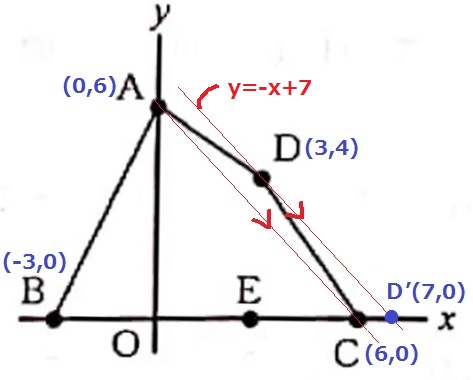
ＡＣの傾きが－１。
Ｄを通る傾き－１の直線をひく。
Ｄから下に４、右に４移動して、直線とｘ軸との交点Ｄ’（７、０）
等積変形で四角形ＡＢＣＤは△ＡＢＤ’に置き換えることができる。
△ＡＢＤ’の底辺はＢとＤ’の距離で10。
底辺を５にすれば、面積が半分になる。
ｘ軸上でＢから距離５の２点は（－８、０）と（２、０）。
（２）
最大数は、100ａ＋10ｂ＋ｃ。
最小数は、100ｃ＋10ｂ＋ａ。
（100ａ＋10ｂ＋ｃ）－（100ｃ＋10ｂ＋ａ）
＝99ａ－99ｃ
＝99（ａ－ｃ）＝396
ａ－ｃ＝４
９≧ａ＞ｃ≧１の条件を加味すると、
（ａ、ｃ）＝（９、５）（８、４）（７、３）（６、２）（５、１）
ｂはａとｃのあいだの数字で、各々３通りずつある。
*例えば、ａ＝９、ｃ＝５であれば、ｂ＝６～８の３通り。
３×５＝15通り
Ⅰ…99（ａ－ｃ）、Ⅱ…15
（３）①
タクシーに乗っていた時間は、15÷36＝５/12時間＝25分
残り３ｋｍを歩いた時間は、３÷４＝３/４時間＝45分
到着時刻は、25＋45＝70分
原点→（25、15）→（70、18）を結ぶ。
②
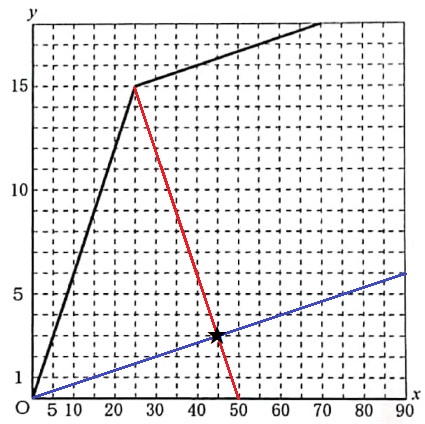
徒歩の傾きは右に３、上に１（１/３）。
タクシーの傾きは右に１、上に３だったので、帰りは右に１、下に３（－３）。
交点を読み取ると45分後。
大問３（図形）
（１）
弧ＡＢの円周角より、∠ＡＤＢ＝65°
△ＡＤＥで外角定理→∠ＤＡＥ＝86－21＝65°
△ＡＢＤの内角から、∠ＡＢＥ＝180－（65×２＋21）＝29°
（２）①
△ＡＢＥと△ＤＥＣを等積変形させると、和が長方形の半分である。
△ＤＥＣの面積は、80÷２－10＝30ｃｍ2
長方形を似たような形で４分割した問題です。
高度な視点の切り替えが要求されています。
②
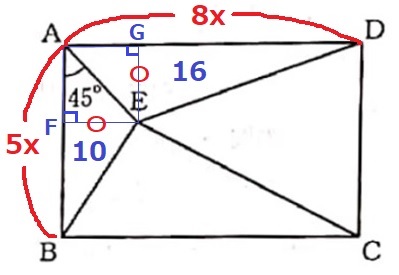
45°を活用する。
ＡＥを対角線とする長方形ＡＦＥＧを作成する。
△ＡＦＥも△ＡＧＥも内角が45°—45°—90°の直角二等辺。
隣り合う辺の長さが等しく、この四角形は正方形である。
△ＡＢＥと△ＡＥＤは高さがＥＦ＝ＥＧで共通なので、
底辺の比であるＡＢ：ＡＤが面積比となる。
ＡＢ：ＡＤ＝10：16＝５：８
ＡＢを５ｘ、ＡＤを８ｘとすると、
５ｘ×８ｘ＝40ｘ2＝80
ｘ＞０より、ｘ＝√２
ＡＢの長さ５ｘ＝５√２ｃｍ。
（３）①
最短距離なので展開図を作成。
１辺が同じ長さの正三角形を組み合わせた図形でＡＤ//ＢＣ。
△ＥＡＨ∽ＥＢＦより、ＥＡ：ＥＢ＝１：２だからＡＨ＝２÷２＝１ｃｍ
△ＡＧＨ∽ＣＧＦより、ＡＧ：ＧＣ＝１：２
ＡＣ＝４ｃｍだから、ＡＧ＝４×１/３＝４/３ｃｍ
②
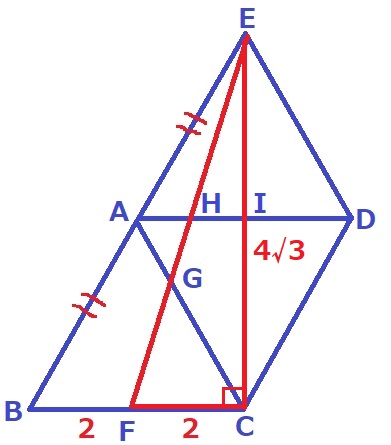
２つの正三角形を組み合わせた四角形ＡＣＤＥは菱形。
Ｅの真下にＣがある。
ＥＣとＡＤの交点をＩとする。菱形の対角線は直交するのでＡＤ⊥ＥＣ。
１辺４ｃｍの正三角形の高さは１：２：√３を利用して、ＥＩ＝ＩＣ＝２√３ｃｍ
ＥＣ＝４√３ｃｍ
△ＥＦＣで三平方→ＥＦ＝２√13ｃｍ
大問１
配点16点
（４）先にａ√ｂの形に変えても良い。
（６）すべて選べだが、やりやすかった。歯車の歯数と回転数も反比例。
（７）ａを使って平均値と中央値を出してみる。
（８）体積＝底面積×高さだから、底面積の比と高さの比が逆比。
大問２
（１）（０、６）（６、０）が気になる。傾き－１から、Ｄをｘ軸に移しやすい。
高さ共通⇒底辺半分。
（２）正答率は高くないと思う。
文字の条件とｂの存在を忘れずに。
（３）愛知はグラフをうまく使うとシャっと解ける問題がでてくるイメージ。
大問３
（２）①中学受験でよく出てくる。
②発想力が問われた。おそらく一番難しい。
45°線は∠ＢＡＤの二等分線で２直線ＡＢ・ＡＤからの距離が等しい。
⇒２つの三角形の高さが等しい、と説明しても良い。
面積比がそのまま長方形の縦：横になるとわかれば、方程式で決着がつく。
（３）①３つの正三角形の作図をうまく描けるか。
雑で下手な絵を描くと真相が見えず、たぶん失敗する。
合同な２つの正三角形をくっつけると菱形になる。
ＡＧはチョウチョ型の相似。ＡＨを別の角度から眺めてみる。
②菱形の対角線が見えたら答えはすぐそこ。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント