平均22.4点（前年比；－0.2点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）（ア）
－４－７
＝－11
（イ）
－２（ｘ＋３ｙ）＋（ｘ－３ｙ）
＝－２ｘ－６ｙ＋ｘ－３ｙ
＝－ｘ－９ｙ
（ウ）
８ｘｙ2÷（－２ｘ）
＝－４ｙ2
（エ）
（√５＋１）2
＝５＋２√５＋１
＝６＋２√５
（２）
ｘ2－９ｙ2
＝（ｘ＋３ｙ）（ｘ－３ｙ）
（３）
２ｘ2－ｘ－２＝０
解の公式を適用して、ｘ＝（１±√17）/４
（４）
側面の扇形の弧と、底面の円の円周の長さは同じ。
中心角の比は、扇形：円＝180：360＝１：２
半径は逆比で、扇形（母線）：円（半径）＝②：①
半径は、４×①/②＝２ｃｍ
（５）
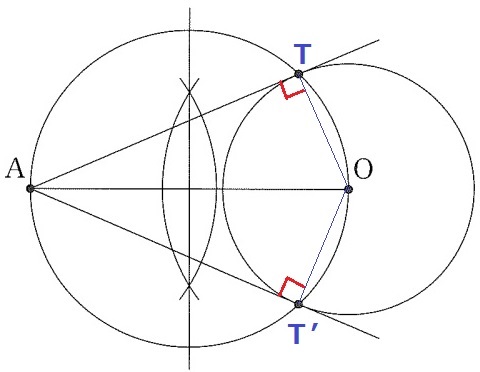
接線と半径は垂直に交わる。
接点をＴ、Ｔ’とすると、∠ＡＴＯ＝∠ＡＴ’Ｏ＝90°
直径に対する円周角は90°。
直径をＡＯとする円を描き、その円と円Ｏが交わる２点がＴ、Ｔ’となる。
①ＡＯの垂直二等分線
②ＡＯの中点からグルっと円を描く。
③Ａから接点に向けて２本の接線をひく。
（６）
Ｂを通る平行線をひく。錯角でｘと44°を移動させる。
△ＡＢＣは二等辺だから、∠ＡＢＣ＝∠ＡＣＢ＝ｘ＋44°
△ＡＢＣの内角より、２（ｘ＋44）＋54＝180
ｘ＝19°
（７）
①：第３四分位数（Q3）が最も大きいのは2012年。×
②：四分位範囲＝Q3－Q1、箱の横の長さで2012年が最も大きい。〇
③：2021年の最小値は18℃だが、第１四分位数（Q1）は23℃。
下から25％のデータ（３か月）の中で20℃以下は複数月あるかもしれない。×
④：2012年のQ3は34℃を超えている。上位25％は34℃以上。〇
⑤：×印などで平均値を示す箱ひげ図もあるが、この図にはない。×
②、④
大問２（方程式＆数量変化）
（１）（ア）
単位を書くと…
ｘ＋ｙ＝1640ｍ
ｘ/(分速60ｍ)＋ｙ/(分速100ｍ)＝22分
ｘは歩いた道のり、ｙは走った道のり（①）。
歩いた速さは分速60ｍ（②）。
別の方程式をつくる。
先ほどは道のりを文字においた。速さは分速60ｍと分速100ｍと決まっている。
残りの要素は時間しかない（③）。
ア
（イ）
歩いた時間をｘ、走った時間をｙとする。
道のりの合計で等式→60ｘ＋100ｙ＝1640
時間の合計で等式→ｘ＋ｙ＝22
④…60ｘ＋100ｙ ⑤…ｘ＋ｙ
（ウ）
前問の連立を解く。
60ｘ＋100ｙ＝1640
ｘ＋ｙ＝22
これを解くと、ｘ＝14、ｙ＝８
ｘは歩いた時間、歩いた道のりは60ｘ＝60×14＝840ｍ
（*最初にユウがつくった連立方程式を解いても良い。
ｘの値がそのまま歩いた道のりになる）
（２）（ア）
３秒後はＰＡ＝３ｃｍ、ＱＡ＝12－２×３＝６ｃｍ
三角錘ＰーＡＢＱ＝６×９÷２×３÷３＝27ｃｍ3
（イ）
Ｑの速さは毎秒２ｃｍ→ＤＱ＝２ｘｃｍ
ＱＡ＝ＤＡ－ＤＱ＝12－２ｘｃｍ
（ウ）
答案ではｘについての方程式をつくり、求める過程を記述する。
ＰＡ＝ｘ、ＱＡ＝12－２ｘを使って三角錘Ｐ－ＡＢＱの体積を求めると、
（12－２ｘ）×９×１/２×ｘ×１/３
＝18ｘ－３ｘ2＝24
３ｘ2－18ｘ＋24＝０ ←÷３
ｘ2－６ｘ＋８
＝（ｘ－２）（ｘ－４）＝０
仮定より０≦ｘ≦６だから、ｘ＝２、４
２秒後と４秒後
大問３（関数）
（１）
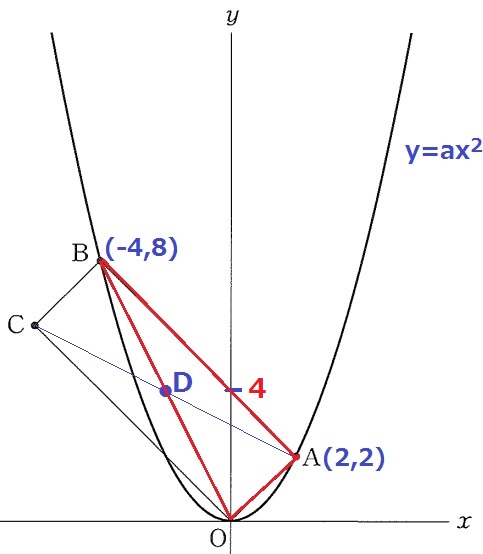
ｙ＝ａｘ2にＡ（２、２）を代入する。
２＝４ａ
ａ＝１/２
（２）
Ｂ（－４、８）→Ａ（２、２）
右に６、下に６だから、傾きは－６/６＝－１
切片はＡから左に２、上に２→２＋２＝４
ｙ＝－ｘ＋４
（３）
平行四辺形の対辺は平行かつ、長さが等しい。
Ａ→Ｏは左に２、下に２。
Ｂ→Ｃも左に２、下に２移動してＣ（－６、６）
（４）（ア）
平行四辺形の対角線はおのおのの中点で交わる。
ＤはＯＢの中点だから、ＯＤ：ＤＢ＝１：１
（イ）
先に△ＯＡＢを求める。
底辺は切片４。高さの合計はＡとＢのｘ座標の差６。
４×６÷２＝12
前問よりＯＤ：ＤＢ＝１：１だから、
△ＯＡＤ＝△ＯＡＢ÷２＝12÷２＝６
（ウ）
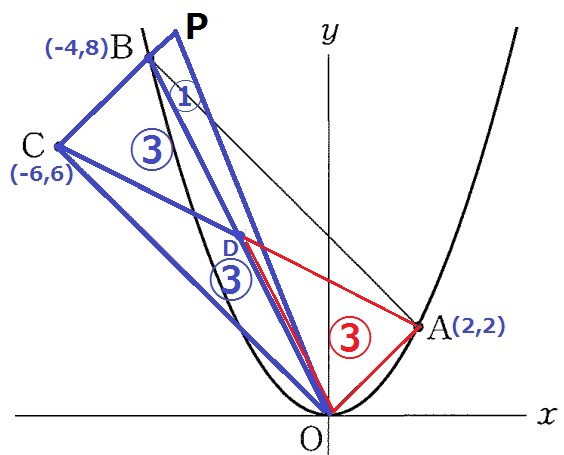
△ＯＡＤと△ＯＰＣの面積をそれぞれ③、⑦とする。
平行四辺形の対角線はその面積を４等分する。
△ＯＤＣ＝△ＤＢＣ＝③→△ＯＢＣ＝⑥
Ｂの右側にＰをおく。
△ＯＰＢ＝△ＯＰＣ－△ＯＢＣ＝①
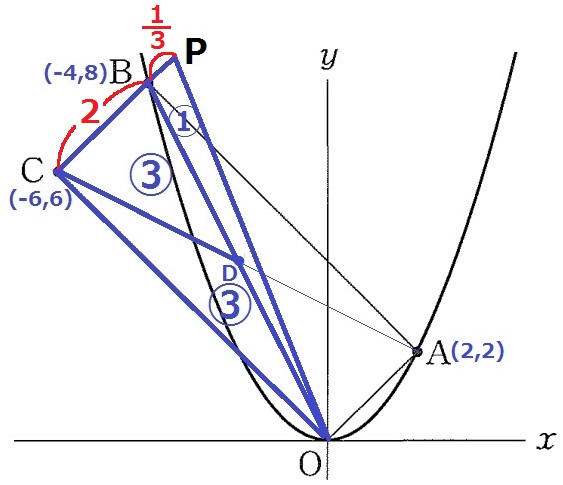
ＣＢ：ＢＰ＝△ＯＢＣ：△ＯＰＢ＝６：１
ＢＣのｘ座標の差は２、ＢＰの差は２×１/６＝１/３
Ｐのｘ座標はＢから右に１/３⇒－４＋１/３＝－11/３
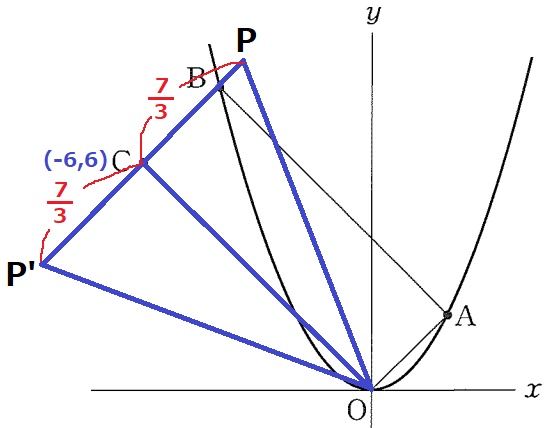
今度はＣの左側にＰ’を置く。
Ｐ’はＣについてＰと対称的な位置関係にある。
Ｐ’のｘ座標は、－６－７/３＝－25/３
－11/３、－25/３
大問４（平面図形）
（１）
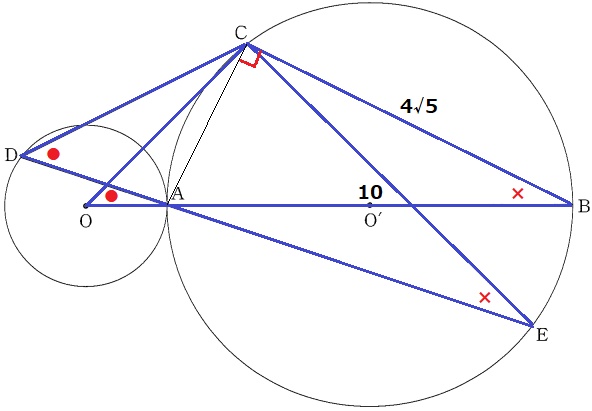
直径ＡＢに対する円周角は90°→∠ＡＣＢ＝90°
△ＡＢＣで三平方、ＡＣ＝２√５ｃｍ
（２）
△ＯＢＣ∽△ＤＥＣの証明。
仮定より、∠ＣＯＡ＝∠ＣＤＡから、∠ＣＯＢ＝∠ＣＤＥ
弧ＡＣに対する円周角で、∠ＣＢＯ＝∠ＣＥＤ
２角相等で∽。
（３）（ア）
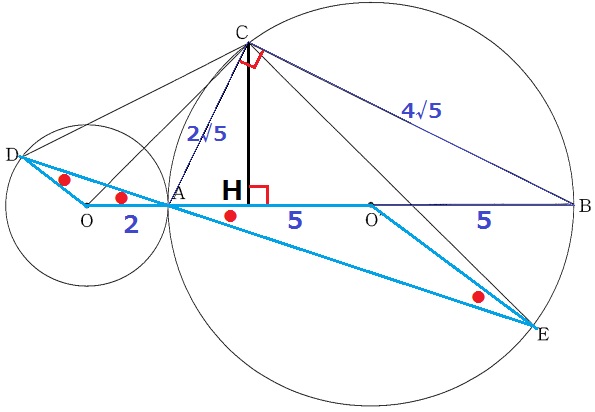
ＣＨは△ＡＢＣの高さにあたる。
△ＡＢＣの面積を２通りで表すと、【ＡＢ×ＣＨ÷２＝ＡＣ×ＣＢ÷２】
ＣＨ＝ＡＣ×ＣＢ÷ＡＢ＝２√５×４√５÷10＝４ｃｍ
（イ）
対頂角で、∠ＤＡＯ＝∠ＥＡＯ’（●）
半径から△ＯＡＤと△Ｏ’ＡＥは二等辺三角形で底角が●で等しい。
２角相等で、△ＯＡＤ（Ｓ）∽△Ｏ’ＡＥ（Ｔ）。
面積比は相似比の２乗。
Ｓ：Ｔ＝２2：５2＝４：25
（ウ）
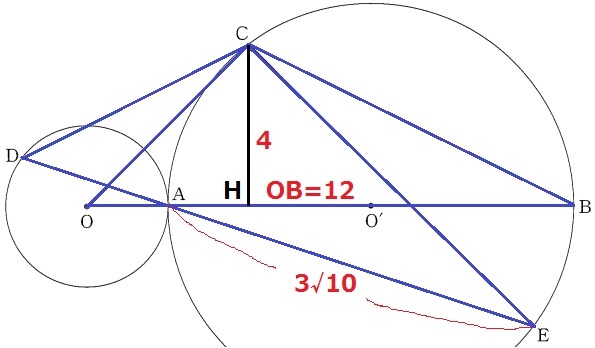
△ＯＢＣの面積は、12×４÷２＝24ｃｍ2
（２）より△ＯＢＣ∽△ＤＥＣだから、相似比がわかれば面積比がでる。
ＯＢに対応する辺であるＤＥの長さをＡＥ＝３√10ｃｍから求められないか。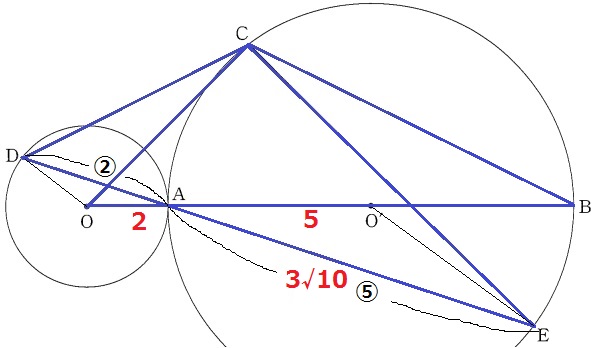
前問より、△ＯＡＤ∽△Ｏ’ＡＥの相似比は②：⑤
ＤＥ＝３√10×⑦/⑤＝21√10/５ｃｍ
△ＯＢＣ：△ＤＥＣの相似比は、ＯＢ：ＤＥ＝12：21√10/５＝60：21√10＝20：７√10
面積比は、202：（７√10）2＝400：490＝40：49
△ＤＥＣの面積は、24×49/40＝147/５ｃｍ2
大問５（確率＆規則）
（１）（ア）
スタートから11マス進む。
Ｄ
（イ）
最大の６＋６＝12マスでも折り返してＣ。
Ａまでは戻れないから、あり得ない。
確率は０！
（ウ）
全体は、６×６＝36通り
Ｆに止まるには５マスか９マスのいずれか。
●和が５
（１、４）（２、３）とこれらの逆で４通り。
●和が９
（３、６）（４、５）とこれらの逆で４通り。
計８通りで、確率は８/36＝２/９
（エ）
Ｈマスに止まらない方が多いので余事象から攻める。
Ｈに止まるには和が７→（１、６）（２、５）（３、４）と逆を含めた６通り
確率は６/36＝１/６
Ｈに止まらない確率は、１－１/６＝５/６
（２）（ア）
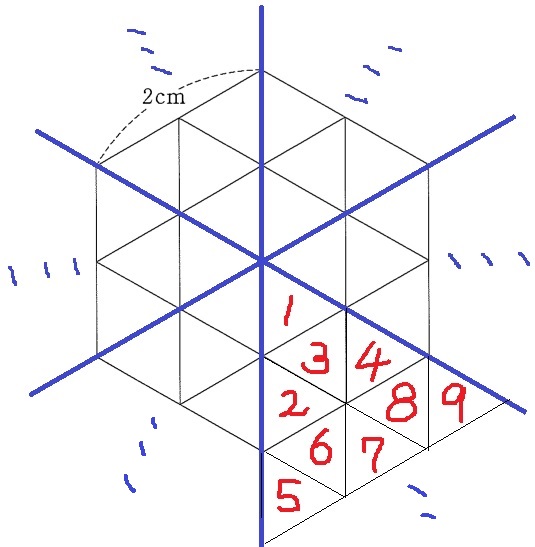
正六角形は対称性がある。
うえのように正六角形を６ピースに区切って考えると、
１ピースは１枚、４枚、９枚…と平方数で増えていく。
１辺３ｃｍの場合、３2×６＝54枚
（イ）
１辺６ｃｍの場合は、６2×６＝216枚
（ウ）
2023÷６＝337…１
１ピースのあたりの枚数は、337以下の最大の平方数。
18×18＝324が最大の平方数だから18ｃｍ。
（*20×20＝400までの平方数は覚えておこう）
前問の利用が多い印象。前半の基本問題は確実にあてる。
大問１
（４）側面の扇形の中心角＝360×半径/母線も覚えておきたい。
中心角が共通→半径に応じて弧は長くなる。
半径が共通→中心角に応じて弧は長くなる。
弧（円周）が共通→半径と中心角の比は逆比
（６）描きやすい作図だが、やり方を知らないと難しいかも。
大問２
（１）道のり・速さ・時間の３要素のうち速さはわかっている。
道のりか時間に文字を割り当てる。
（２）毎秒２ｃｍ→２ｘｃｍになる！某県で正答率が悪かった。
（ウ）辺の長さをｘで表して三角錐の体積を求める。
大問３
（３）このタイプは公立入試でたびたび見かける。
（４）（イ）前問の誘導を用いて、ここまでは取りたい。
（ウ）差がつく。面積比をうまく使う。
大問４
（３）（ア）差がつきそうな予感。
ＣＨは三平方ではなく、△ＡＢＣの高さから算出する。
（ウ）相似から面積比の利用。
使っていない３√10からＤＥが求められないかと発想する。
比の計算も慎重に！
大問５
３・４より解きやすい。
（１）（イ）確率ゼロもあるよ！
（２）６分割が見えれば全問正解を狙える。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント