2023年度　宮崎県公立高校入試問題過去問【数学】解説

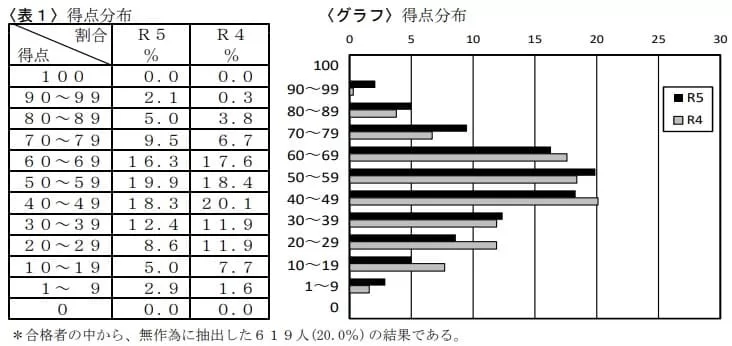
平均52.1点（前年比；＋3.6点）
最高点―100点、最低点―０点

問題ＰＤＦ

大問１（小問集合）－70.3％

（１）　97.4％
－２＋７
＝５

（２）　93.2％
－３/４×２/15
＝－１/10

（３）　87.1％
√50＋√８－√18
＝５√２＋２√２－３√２
＝４√２

（４）　72.7％
－ａ＋３ｂ＝１
３ｂ＝ａ＋１
ｂ＝（ａ＋１）/３

（５）　86.6％
ｙ＝ｘ－６　…①
３ｘ＋４ｙ＝11　…②

①を②に代入すると、３ｘ＋４（ｘ－６）＝11
７ｘ＝35
ｘ＝５
①に代入、ｙ＝５－６＝－１
（ｘ、ｙ）＝（５、－１）

（６）　31.0％！
９ｘ²＝５ｘ
９ｘ²－５ｘ
＝ｘ（９ｘ－５）＝０
ｘ＝０、９ｘ－５＝０→ｘ＝５/９
ｘ＝０、５/９

（７）　68.7％
ア：半分以上が30℃以上なのは、中央値が30℃である2021年。×
イ：×印などで平均値を表す箱ひげ図もあるが、本問にはない。×
ウ：２つとも第１四分位数が25℃を超えている。
（これは下位15日の真ん中、下から８番目の値が25℃超）
最小値よりどちらも25℃以下が１日ずつあるのは確定だが、それ以外の情報は不明。×
エ：散らばりの程度→範囲（レンジ）＝最大値－最小値、2021年の方が小さい。〇
エ

（８）　25.8％！
回転の中心の作図。

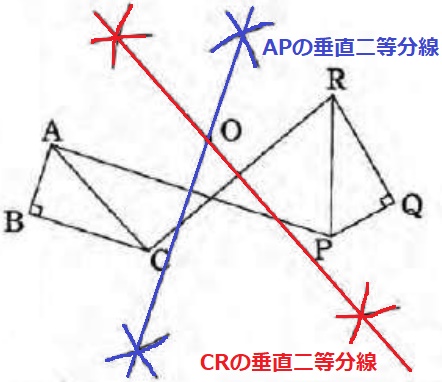
ＡとＰ、ＣとＲが対応する点。
これらを結んだ線分の垂直二等分線の交点が回転の中心Ｏ。
（*ＢＱでもＯＫ）

大問２（確率・方程式）－59.4％

【１】（１）　85.7％
１回目に”何か”を出す。
２回目にその”何か”を再び出す確率は５枚中１枚。
１/５

（２）　52.2％
答案では確率を使って説明を書く。
全体は５×５＝25通り
数の重複が許される点に注意！
ア：４の倍数→12、16、24、44、64、92、96の７通り。
イ：６の倍数→12、24、42、66、96の５通り。
確率を比較すると７/25＞５/25だから、アの方が起こりやすい。

【２】（１）　68.3％
カレーは２人分、肉じゃがは５人分。
１人あたりのｇに直すと、
カレー：100÷２＝50ｇ
肉じゃが：600÷５＝120ｇ
50ｘ＋120ｙ

（２）①…46.0％、②…49.3％
●じゃがいも
50ｘ＋120ｙ＝1120　…【1】
●玉ねぎ
同様に１人あたりに直すと、65ｘ＋50ｙ＝820　…【2】

この連立を解けばいいが係数が面倒くさい(;`ω´)
【1】÷10で、５ｘ＋12ｙ＝112　…【3】
【2】÷５で、13ｘ＋10ｙ＝164　…【4】

【4】×６－【3】×５をすると、53ｘ＝424
ｘ＝８
【3】に代入して、ｙ＝６
①…８、②…６

大問３（関数）－42.9％

【１】　84.3％
ｙ＝１/４ｘ²にｘ＝－６を代入。
ｙ＝１/４×（－６）²＝９

【２】　59.5％
Ａ（－６、９）→Ｂ（４、４）
右に10、下に５だから、傾きは－５/10＝－１/２
切片はＢから左に４、上に２移動して、４＋２＝６
ｙ＝－１/２ｘ＋６

【３】（１）　22.0％！

ＣとＤのｘ座標はｔ。
Ｃは直線ℓ上の点→ｙ座標は－１/２ｔ＋６
Ｄは放物線上の点→ｙ座標は１/４ｔ²
ＣＤ＝（－１/２ｔ＋６）－１/４ｔ²
＝－１/４ｔ²－１/２ｔ＋６

（２）　13.2％！
長方形から正方形になる→隣り合う辺の長さが等しくなる。
ＥＤはｘ軸と平行→放物線上のＥとＤはｙ軸について対称な点→Ｅのｘ座標は－ｔ
ＥＤ＝２ｔ

ＣＤ＝ＥＤ
－１/４ｔ²－１/２ｔ＋６＝２ｔ　←４倍
－ｔ²－２ｔ＋24＝８ｔ
ｔ²＋10ｔ－24
＝（ｔ＋12）（ｔ－２）＝０
０＜ｔ＜４だから、ｔ＝２

Ｃのｘ座標は２、これをｙ＝－１/２ｘ＋６に代入するとｙ＝５
Ｃ（２、５）

大問４（平面図形）－29.1％

【１】　68.8％

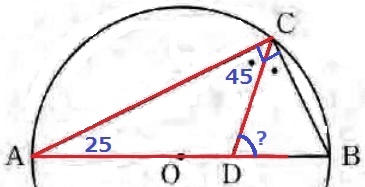
半円の弧に対する円周角は90°→∠ＡＣＤ＝90÷２＝45°
△ＣＡＤで外角定理→∠ＣＤＢ＝45＋25＝70°

【２】（１）　32.1％！
△ＢＣＤ∽△ＤＢＦの証明。

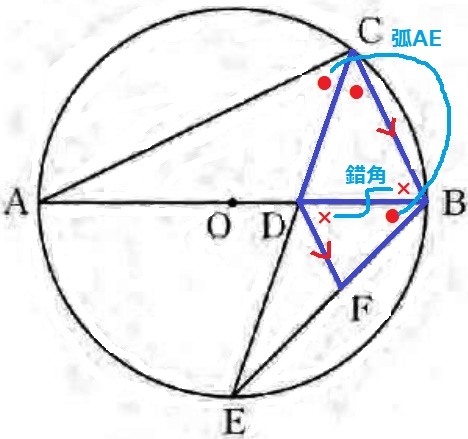
ＣＢ//ＤＦの錯角より、∠ＣＢＤ＝∠ＢＤＦ（●）
仮定よりＣＤは∠Ｃの二等分線＋弧ＡＥに対する円周角で、
∠ＢＣＤ＝∠ＤＢＦ（×）
２角相等で∽。

（２）　19.8％！

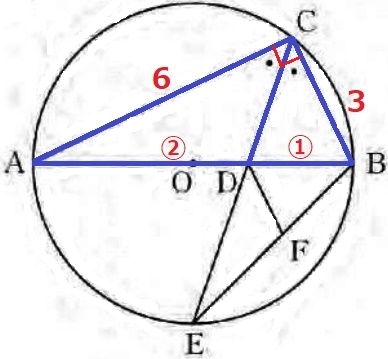
公立入試でも角の二等分線の定理はおさえておきたい。
ＣＡ：ＣＢ＝ＡＤ：ＢＤ＝②：①
△ＡＢＣで三平方→ＡＢ＝３√５ｃｍ
ＤＢ＝３√５×①/③＝√５ｃｍ

（３）　1.7％!!

△ＤＥＦは下にある。
ＣＢ//ＤＦ→△ＣＥＢ∽△ＤＥＦを足掛かりにする。
相似比を知るために、ＣＢに対応するＤＦの長さが知りたい。

ここで、（１）の相似を使う。
△ＢＣＤ∽△ＤＢＦより、ＣＢ：ＢＤ＝ＢＤ：ＤＦ＝３：√５
ＤＦ＝√５×√５/３＝５/３ｃｍ

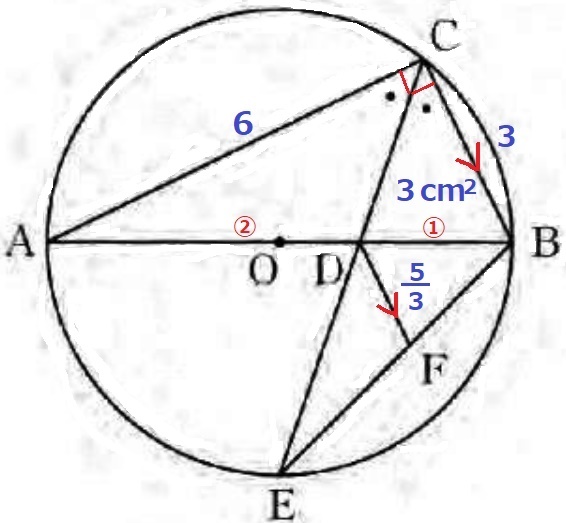
面積がすぐ出るのは△ＡＢＣ。
（２）よりＡＤ：ＤＢ＝△ＡＤＣ：△ＢＤＣ＝②：①だから、
△ＢＤＣの面積は、６×３÷２×①/③＝３ｃｍ²

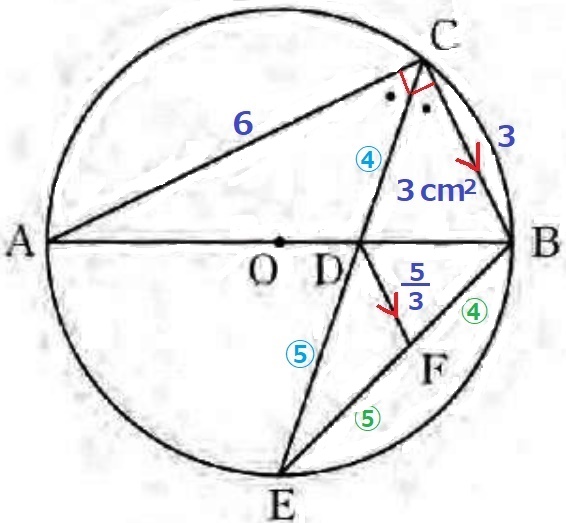
△ＣＥＢ∽△ＤＥＦの相似比は、ＣＢ：ＤＦ＝３：５/３＝９：５
ＣＤ：ＤＥ＝△ＢＤＣ：△ＢＤＥ＝④：⑤
（△ＢＤＣ×⑤/④＝△ＢＤＥ）
ＢＥ：ＦＥ＝△ＢＤＥ：△ＤＥＦ＝⑨：⑤
（△ＢＤＥ×⑤/⑨＝△ＤＥＦ）
△ＤＥＦの面積は、３×⑤/④×⑤/⑨＝25/12ｃｍ²

大問５（空間図形）－31.4％

【１】　82.9％

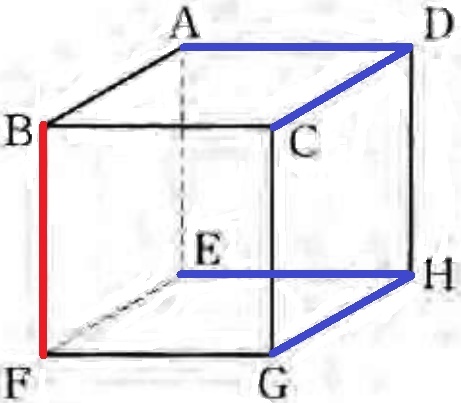
ネジレ→平行ではない、かつ延長しても交わらない（同一平面上にない）
ＢＦとネジレはＡＤ、ＥＨ、ＣＤ、ＧＨの４本。

【２】　29.0％！

△ＣＦＨの各辺は立方体の面である正方形の対角線。
３辺の長さは等しく、△ＣＦＨは正三角形。
△ＦＧＨは直角二等辺、辺の比は１：１：√２→ＦＨ＝６√２ｃｍ
１辺が６√２ｃｍの正三角形の高さ→１：２：√３を使って、３√２×√３＝３√６ｃｍ
面積は、６√２×３√６÷２＝18√３ｃｍ²

【３】　11.5％！

ＰはＡ→Ｂ、ＱはＧ→Ｈを同じ速さで移動する。
線分ＰＱのスタート時はＡＧ（青）、ゴール時はＢＨ（赤）、真ん中は水色で、
いずれも面ＡＢＧＨ上にある線分である。

ＡＢ⊥面ＢＦＧＣ⊥ＨＧ→∠ＡＢＧ＝∠ＨＧＢ＝90°
四角形ＡＢＧＨはＡＢ＝６ｃｍ、ＢＧ＝６√２ｃｍの長方形。

対角線ＡＧとＢＨの交点Ｏは長方形の中心で、求積すべき図形は△ＯＡＢ＋△ＯＧＨ。
長方形の対角線は面積を４等分するので、長方形の半分に当たる。
６×６√２÷２＝18√２ｃｍ²

【４】　2.3％!!

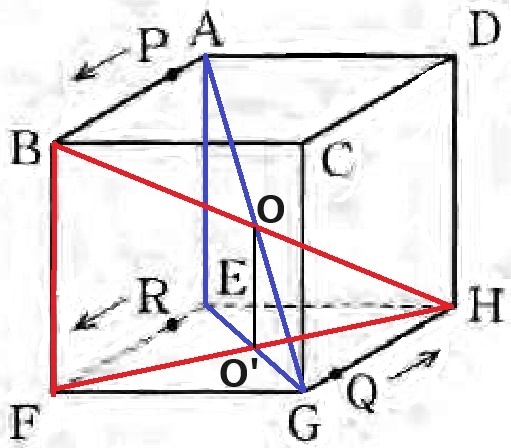
線分ＰＲと点Ｑを移動させる。
スタート時は△ＡＥＧ（青）、ゴール時は△ＢＦＨ（赤）
立方体の対角線ＡＧとＢＨの交点Ｏは立方体の中心である。
Ｏの真下をＯ’とすると、求積すべき立体は三角錘Ｏ―Ｏ’ＧＨ＋立体ＯＯ’―ＡＢＦＥ。

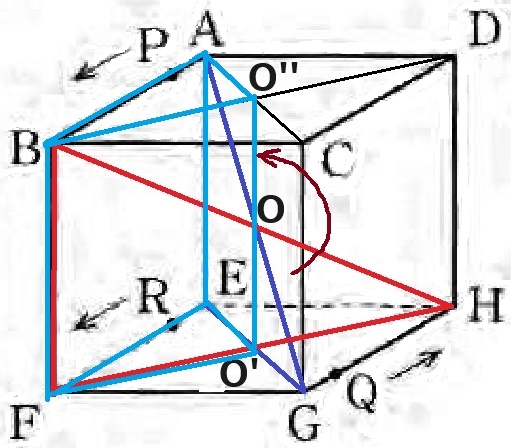
Oの真上をO”とする。
ＯはＡＧ、ＢＨ、Ｏ’’Ｏ’の中点で、Ｏに対してＡとＧ、ＢとＨ、Ｏ’’とＯ’は対称である。
ということは、三角錐Ｏ―Ｏ’ＧＨをひっくり返して三角錐Ｏ―Ｏ’’ＡＢにはめ込むと、
求積すべき体積は三角柱Ｏ’’ＡＢ―Ｏ’ＥＦに変形することができる。

△Ｏ’’ＡＢの面積は正方形ＡＢＣＤの４分の１⇒三角柱の体積は立方体の４分の１。
したがって、６³÷４＝54ｃｍ³