2019年度　福岡県公立高校過去問【数学】解説

平均；53.1％
問題はコチラから→ＰＤＦファイル

大問１（小問集合）－86.1％

（１）　97.2％
７＋３×（－４）
＝７－１２＝－５

（２）　90.9％
４（２ａ－３ｂ）－（ａ＋２ｂ）
＝８ａ－１２ｂ－ａ－２ｂ
＝７ａ－１４ｂ

（３）　92.2％
√４５－２５/√５
＝３√５－５√５＝－２√５

（４）　91.7％
５ｘ－２＝２（４ｘ－７）
３ｘ＝１２
ｘ＝４

（５）　89.2％
ｘ（ｘ－１）＝３（ｘ＋４）
ｘ²－４ｘ＋１２＝０
（ｘ－６）（ｘ＋２）＝０
ｘ＝－２、６

（６）　87.1％
ａ＝ｘｙ＝３×８＝２４
ｙ＝２４/ｘ＝２４/（－２）＝－１２

（７）　64.8％
傾きが負なので上に凸のグラフ。
原点、（２、－１）、（４、－４）が通るように放物線を描く。

（８）　72.8％
◆１年生
100人の中央値は、50人目と51人目の平均
下から計算していくと、50人目と51人目はともに〔10以上～15未満〕がある。

◆３年生
105人の中央値は、（105＋１）÷２＝53人目
53人目は〔５以上～10未満〕。
したがって、中央値が大きいのは１年生で、階級は〔10以上～15未満〕

（９）　88.6％
50人中、関心のある生徒は35人。
400人では、35×400/50＝280人

大問２（確率）－58.5％

（１）　54.0％
全て選べ式だが、落ち着いて解けば大丈夫。
完全な予知はできないので、絶対にこうと断言しているものは×。
あくまでもこのような可能性があるとしか言えない。
イ・エ

（２）　60.3％
説明問題。
どちらが当たるか比べるので、ＡとＢの確率をそれぞれ求めて比較する。
Ａは１回目の玉を袋に戻すが、Ｂは戻さないことに注意！
◆くじ引きＡ◆
〔赤→白で出す〕
２/３×１/３＝２/９
〔白→赤で出す〕
１/３×２/３＝２/９
項をひっくり返しただけで一緒。
２/９×２＝４/９
◆くじ引きＢ◆
３個のうち、２つの赤をとるので、２/３

大小関係を比較。
４/９＜２/３なので、くじ引きＢの方が当たりやすい。
公式解答では樹形図で丁寧に調べている。

大問３（文字式）－40.3％

（１）　82.3％
３ａ－１のａに１２を放り込む。
３×１２－１＝３５

（２）　29.4％！
説明問題。
〔最初に決めた数〕→ａ
〔手順通りに求めた数〕→３ａ－１
本問は、３ａ－１の値がわかっている場合、そこからａを求める。
３ａ－１＝□
ａ＝（□＋１）÷３
１を足して、３で割ればａがでる。

（３）　23.1％！
変化球があって困惑する(;´Д｀)
ある数で割るだけでａがでるということは、定数項がない。
④4ａ－４　→　⑤Ａ　→　⑥＋ａ＋１

１つ目は、÷４をする。
－４を÷４すると－１となり、＋１で定数項がなくなる。
（４ａ－４）÷４＋（ａ＋１）＝２ａ
解答…Ａ＝④の数を４で割る、Ｂ＝２

２つ目は、＋３をする。
－４＋３＋１＝０となる。
（４ａ－４）＋３＋（ａ＋１）＝５ａ
解答２…Ａ＝④の数に３を足す、Ｂ＝５

大問４（数量変化）－45.4％

（１）　73.2％
表から、Ａは１分間に80ｍ進む。
９分間で、80×9＝720ｍ進むので、
2100－720＝1380ｍ

（２）　66.1％
９～23分でＡは分速60ｍだから、これより速く歩くＢは傾きが急になる→アは×
14分間でＢは、75×14＝1050ｍ進む。
学校までの距離は、1700－1050＝650ｍ→イ

（３）　25.9％！
説明問題。

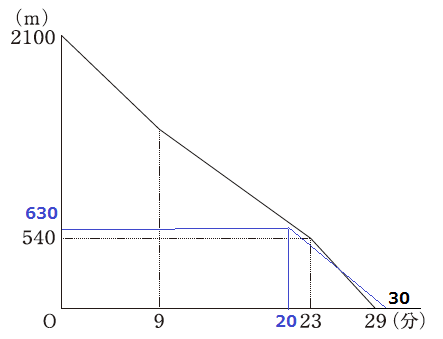
↑Ｃをグラフで表すとこんな感じ。
ＡとＣのグラフが重なる時刻を求める。
23～29分のＡは分速90ｍより、傾きが－90で（29、0）と通る。
一次方程式の一般式ｙ＝ａｘ＋ｂに代入して、切片を頑張って求める。
ｙ＝－90ｘ＋2610…①

Ｃは10分間で630ｍ進む→傾き－63ｍ
（20、630）（30、0）の点を通り、同様に式を求める。
ｙ＝－63ｘ＋1890…②

①と②を連立。ｘ＝80/３、ｙ＝210
80/３分＝26・２/３分＝26分40秒
スタートが7：30なので、ＣがＡに追いつかれた時刻は7：56：40となる。

＠余談＠
本問は条件指定があるので使えませんが…
グラフを求めて連立で解くという高校入試テッパンの解法は切片と連立の処理が面倒くさい…。
追いついた時間だけを求めるのであれば中学受験のやり方をオススメします。

↑グラフ上で相似を活用。
23分のＣ（青線）の場所を求める。
相似比から、△７＝630×７/１０＝441ｍ
23分のとき、ＡとＣの距離は、540－441＝99ｍ離れている。
Ａは分速90ｍ、Ｃは分速63ｍで同じ方向に歩くので、
１分あたり、90－63＝27ｍずつ近づいていく。
99÷27＝３・２/３＝３分40秒
23分＋３分40秒＝26分40秒
こちらの方が計算しやすいのでミスも少なくなるかと。

大問５（平面図形）－36.1％

（１）　58.5％
ＡＤ、ＡＥを１辺として、合同っぽい三角形を見つける。
△ＡＤＢ≡△ＡＥＣ

（２）　46.2％
△ＡＤＥ∽△ＡＢＣの証明。

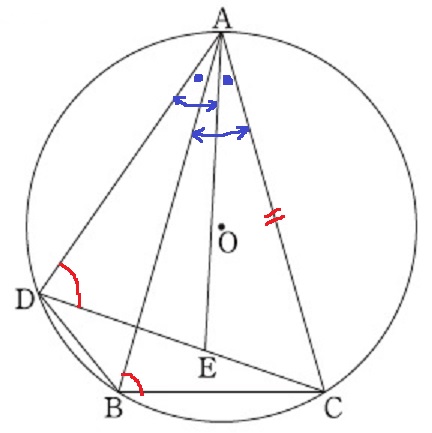
∠ＡＢＥをはさんで、∠ＤＡＥ＝ＢＡＣ
孤ＡＣの円周角より、∠ＡＤＥ＝∠ＡＢＣ
２角が等しい→∽

（３）　4.3％!!
円の中心Ｏが図形の線上にない。
→半径４ｃｍは正三角形ＡＢＣの一辺の長さを求めるうえで活用する。

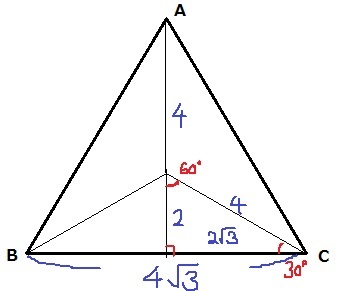
Ｏは正三角形ＡＢＣの重心にある。
上のように補助線をひくと、30°－60°－90°の直角三角形が表れる。
ＢＣ＝４√３

前問より、ＡＤ＝ＡＥ

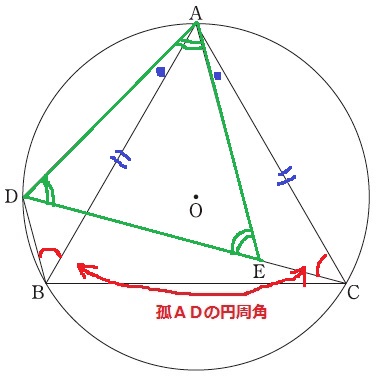
∠ＢＡＣ＝60°で、
∠ＢＡＣ＝∠ＢＡＥ＋●＝∠ＤＡＥだから、
∠ＤＡＥ＝60°→△ＡＤＥは正三角形

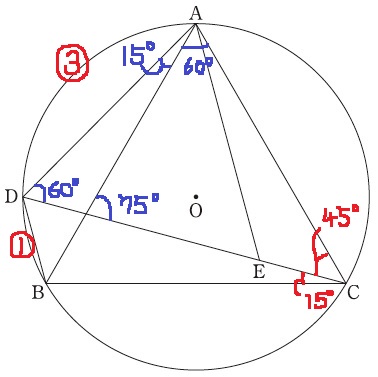
弧ＡＤ：弧ＤＢ＝３：１
円周角である∠ＡＣＤ：∠ＤＣＢも３：１
∠ＡＣＤ＝60×３/４＝４５°
△ＡＤＣ内部の角度を調査していくと、上のようになる。
△ＡＤＣは75°－60°－45°の三角形。

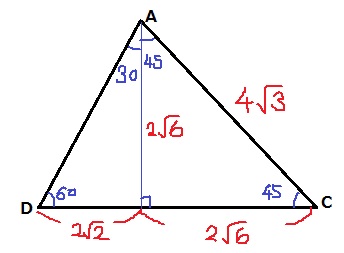
Ａから垂線を下すと、左が30°－60°－90°、右が45°－45°－90°の三角形。
ＡＣ＝４√３から、１：１：√２より、２√６
左の三角形で１：２：√３を用いて、△ＡＤＣの底辺と高さがでる。
△ＡＤＣ＝（２√２＋２√６）×２√２÷２
＝１２＋４√３ｃｍ²
有名な角度の活用方法は覚えておきたい。

大問６（空間図形）－17.3％

（１）　41.5％
６×６×π×５＋６×６×π×４×１/３
＝180π＋４８π
＝228πｃｍ³

（２）　24.3％！
△ＡＢＧ∽△ＡＣＦで、ＡＢ：ＡＣ＝４：９
面積比は辺の比の２乗だから、
△ＡＢＧ：△ＡＣＦ＝16：81
→16/81倍

（３）　1.6％!!

ＭＦを図示。ＭＦを１辺とする、手頃な図形を探す。
ＭＦを対角線とする直方体をみる。
*直方体（ａ×ｂ×ｃ）の対角線→√（ａ²＋ｂ²＋ｃ²）

∠ＤＢＥ＝120°をうまく使うこと！△ＤＢＥに着目。

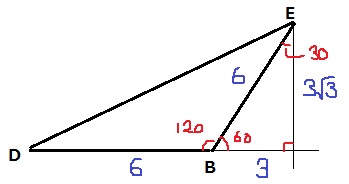
Ｅから垂線を下ろし、ＢＥを斜辺とする直角三角形を作図する。
１：２：√３から、３と３√３がでる。

ここさえ乗り切れば、各辺の長さが求められる。
ＭがＡＤの中点なので、上方の高さ（ＭＨ）は、４（ＡＢ）÷２＝２
高さ･･･２＋５＝７ｃｍ

横の左側（ＭＩ）は、６（ＤＢ）÷２＝３
右側（ＢＪ）は先ほど求めた３なので、
横･･･３＋３＝６ｃｍ
奥行きＪＥは３√３ｃｍ

従って、√{７²＋６²＋（３√３）²}
＝√112＝４√７ｃｍ
公立高校入試解説ページに戻る