2019年度　京都府立高校過去問【前期】数学解説

問題はコチラ→リセマムさん
京都中期はコチラ。

大問１（小問集合）

（１）
{５－（－２²）}÷（３/４）²
＝{５－（－４）}÷９/１６
＝９×１６/９＝１６

（２）
（７ｘ－１）/５－ｘ＋２
＝（７ｘ－１－５ｘ＋１０）/５
＝（２ｘ＋９）/５

（３）
（３－√５）²＋１０/√５
＝９－６√５＋５＋２√５
＝－４√５＋１４

（４）
式を整理したあとに代入。
（ａ－２ｂ）²－２（ａ－２ｂ）－２４　←（ａ－２ｂ）をラージエックスと置く
＝Ｘ²－２Ｘ－２４
＝（Ｘ－６）（Ｘ＋４）　←元に戻す
＝（ａ－２ｂ－６）（ａ－２ｂ＋４）
＝｛３０－２×（－２３）－６｝｛３０－２×（－２３）＋４｝
＝７０×８０＝5600

（５）
解の公式
ｘ＝〔３±√{（－３）²－４・３・（－２）}〕/2・３
＝（３±√３３）/６

（６）
面積比がＡ：Ｂ＝９：１
辺（半径）の比は、Ａ：Ｂ＝３：１
４×３/１＝１２ｃｍ

（７）
実際に描いてみよう。グラフは上に凸になる。

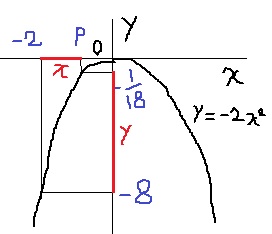
原点を通ってしまうと、ｙの最大値が０になってしまうので、
上のようになる。
ｘ＝－２のとき、ｙ＝－８（ｙ＝－２ｘ²に代入して確認）
ｘ＝ｐのとき、ｙ＝－１/１８となる。
－１/１８＝－２ｐ²
ｐ²＝１/３６
ｐ＝±１/６
ｐ＜０なので、ｐ＝－１/６

（８）
小数第２位を四捨五入したとき、3.1になる範囲。
3.０５≦ａ＜３．１５
3.15は含まないことに注意！
Ａ…ア　Ｂ…ク

（９）

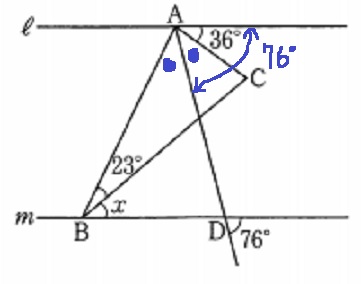
同位角から76°を上に移動。
●＝７６－３６＝４０

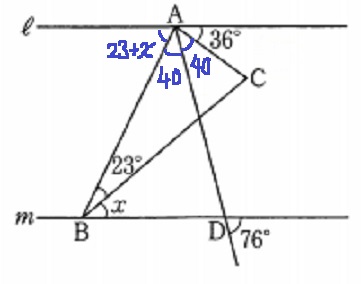
錯角から23とｘをまとめて上に移動させる。
ｘ＝１８０－２３－４０×２－３６
＝４１°

大問２（確率）

（１）
＠ルール確認＠
２つのサイコロを振り。、同数だと１個だけ入れる。
異なる数は２個入れて、間の箱にも入れる。
「６個の箱すべてに玉」→１と６を出す。
（１、６）と（６、１）の２通りあるので、
１/６×１/６×２＝１/１８

（２）
４の箱に入れる方より、入れない方が組み合わせが少ないので、
素直に４に入れない組み合わせを考える。
〔１～３〕の世界と〔５・６〕の世界で場合分け。
・異なる数がでる。
　〔１～３〕
（１、３）（１、２）（２、３）
（１）と同様に各々１/１８だから、１/１８×３＝１/６
　〔５・６〕
（１）と同様、１/１８
計…１/６＋１/１８＝２/９
・同じ数がでる。
４以外で同数が５通り。
１/６×１/６×５＝５/３６
よって、２/９＋５/３６＝１３/３６

大問３（関数）

（１）
ｙ＝ａｘ²より、Ｂの座標は（６、３６ａ）
これが、ＯＢ；y＝３/２ｘを通る。
３６ａ＝３/２×６
３６ａ＝９
ａ＝１/４

（２）
ｙ＝１/４ｘ²に代入。
Ａ（－３、９/４）　Ｂ（６、９）
この２点を通る直線の式が答え。
ｙ＝ａｘ＋ｂに代入。
９/４＝－３ａ＋ｂ　…①
９＝６ａ＋ｂ　…②
連立方程式を解いて、ａ＝３/４　ｂ＝９/２
ｙ＝３/４ｘ＋９/２

（３）
まずは△ＯＥＤの作図。

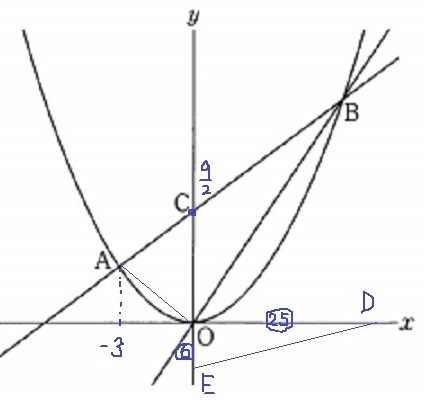
第４象限（右下）に△ＯＥＤができる。
傾きが６/２５なので、ＯＤ＝㉕＝25ｋ、ＯＥ＝⑥＝6ｋとする。
△ＯＣＡ＝△ＯＥＤから、
３×９/２÷２＝25ｋ×６ｋ÷２
150ｋ²＝２７/２
ｋ²＝９/100
ｋ＞０より、ｋ＝３/１０
㉕…２５×３/１０＝１５/２
⑥…６×３/１０＝９/５
Ｄ（１５/２、０）Ｅ（０、－９/５）

大問４（空間図形）

（１）
三角柱じゃないよ！求めるのは三角錐ＡＢＣＥ。
６√２×６√２×１/２×６×１/３＝７２ｃｍ³

（２）
△ＡＢＣは直角二等辺なので、１：１：√２からＡＢ＝１２ｃｍ

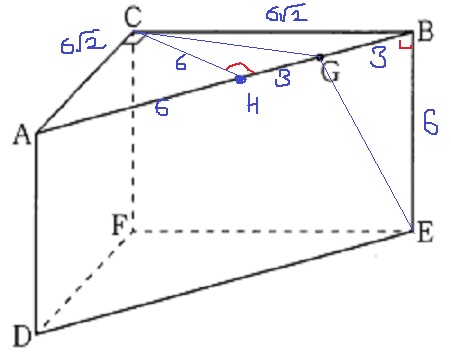
ポイントはＡＢの中点ＨとＣを結ぶ。
ＧＥ＝√（６²＋３²）
＝√４５＝３√５ｃｍ

上の図で△ＣＨＧと△ＥＢＧが合同（二辺と間の角が同じ）なので、
ＣＧ＝ＥＧ＝３√５ｃｍ

△ＣＥＧは二等辺になる。
ＣＥは△ＢＣＥで三平方→６√３
Ｇから垂線を下ろし、二等辺の高さを三平方で出すと３√２
６√３×３√２×１/２＝９√６ｃｍ²

（３）
求める場所がどこかを把握するのが第一関門(;`ω´)

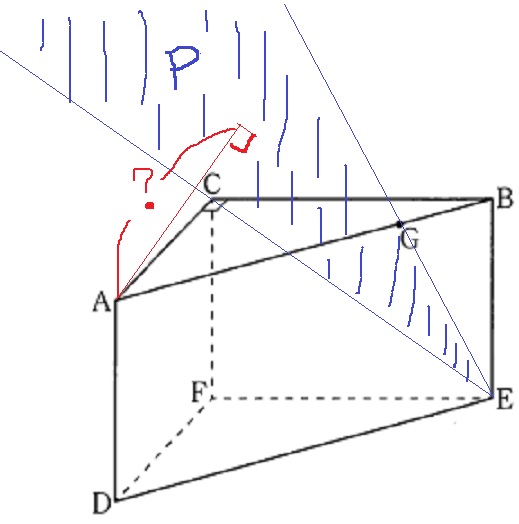
わかりやすいように半直線ＥＣ・ＥＧをひき、間に青い斜線をひいて面Ｐと書きましたが、
Ｃ・Ｅ・Ｇを通る平面Ｐはこれに限らず、青い斜線の面とペタっと接する面すべてが面Ｐです。
（すべての面Ｐをヴィジュアル化するのができなかったので、便宜上三角形の形にしました…）
求める場所は、この面ＰとＡの距離。？のところ。

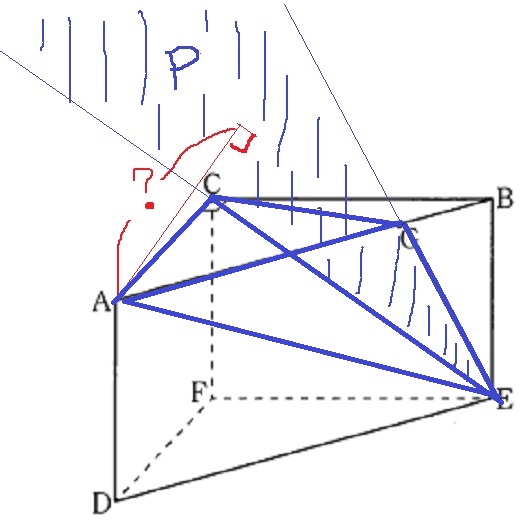
三角柱の中の図形に引きなおして考える。
すると、？は三角錐Ａ－ＣＥＧで底面を△ＣＥＧにしたときの高さに相当する。
△ＣＥＧの面積は前問で求めているので、三角錐Ａ－ＣＥＧの体積がわかればいい。

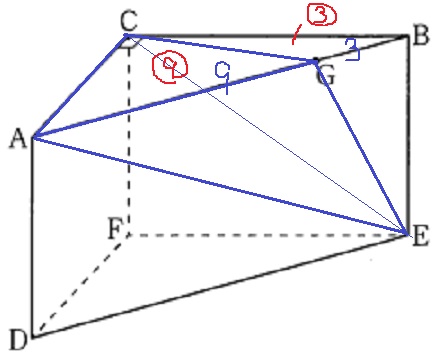
ここで（１）を使う。
今度は、三角錐Ａ－ＣＥＧの底面を△ＡＧＣで捉える。
三角錐Ｅ－ＡＢＣが７２ｃｍ³。
Ｅ－ＡＢＣ：Ｅ－ＡＧＣ（Ａ－ＣＥＧ）の体積比は、
△ＡＢＣ：△ＡＧＣの面積比に相当し、
これはＡＢ：ＡＧ＝１２：９＝４：３と同じである。
よって、Ｅ－ＡＧＣ（Ａ－ＣＥＧ）＝７２×３/４＝５４ｃｍ³
５４×３÷９√６＝３√６ｃｍ
求める場所は与えられた図形のなかの何にあたるか。立体の底面は途中で視点を変える。

大問５（平面図形）

（１）
△ＡＢＤと△ＡＣＦの合同証明。

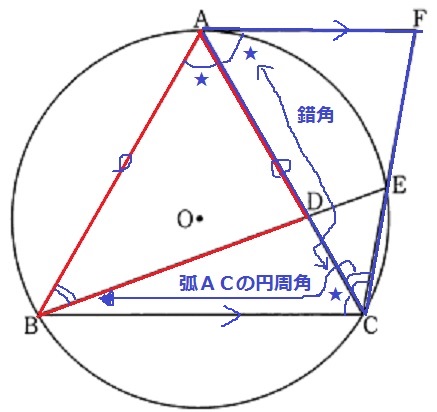
正三角形の１辺＋円周角＋正三角形の１つの角と錯角
＝二辺と間の角が等しい。

（２）
円Ｏは正三角形ＡＢＣの重心。

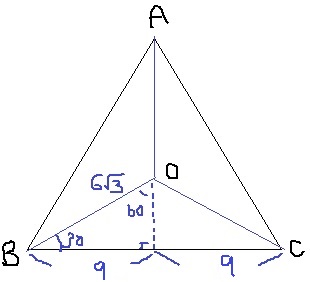
30－60－90〔１：２：√３〕の直角三角形から、
正三角形の１辺は１８ｃｍ。
高さも求めておこう。
〔１：２：√３〕から、１８×√３/２＝９√３
また、重心は中線を２：１に内分することから、６√３×３/２＝９√３と出してもＯＫ。

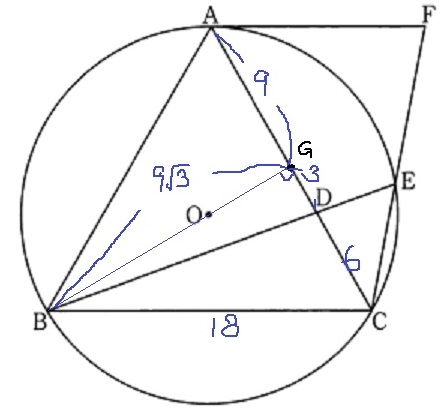
ＡＣの中点をＧとおく。
△ＢＤＧで三平方。ＢＤ＝√{（９√３）²＋３²}＝√252＝６√７ｃｍ

（３）

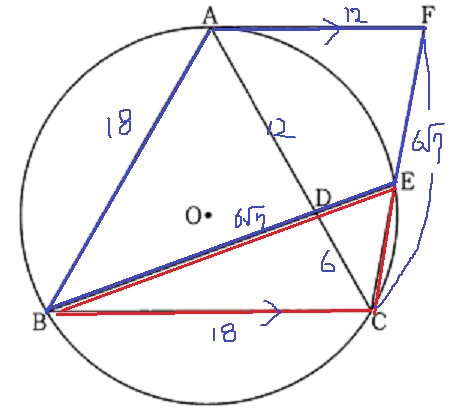
（１）の合同を手がかりに、わかるところを書いていく。
青と赤の面積比なので、中途半端なところにあるＥの場所を特定したい。

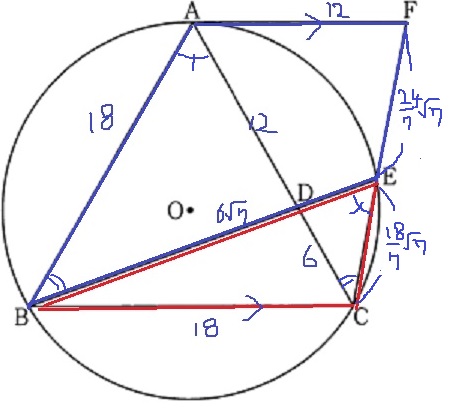
△ＡＢＤ∽△ＥＣＤ（円周角やら対頂角やら）
ＥＣ＝１８×６/６√７＝１８/７・√７
ＥＦ＝６√７－１８/７・√７＝２４/７・√７
比にすると、ＣＥ：ＥＦ＝１８/７・√７：２４/７・√７＝３：４

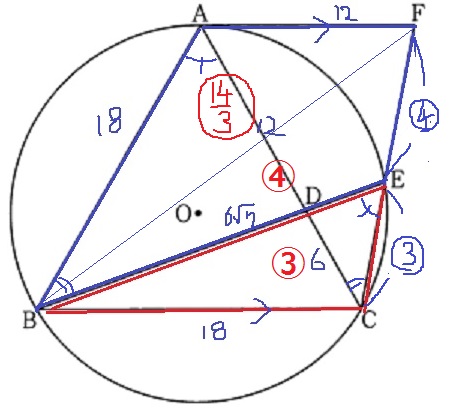
△ＢＣＥ＝③、△ＢＥＦ＝④。
ＡＦ：ＢＣ＝１２：１８＝２：３を利用。
△ＡＢＦ＝△ＢＣＦ×２/３＝⑦×２/３＝○１４/３
したがって、四角形ＡＢＥＦ：△ＢＣＥ
＝１４/３＋４：３
＝２６/３：３
＝２６：９

＠別解＠

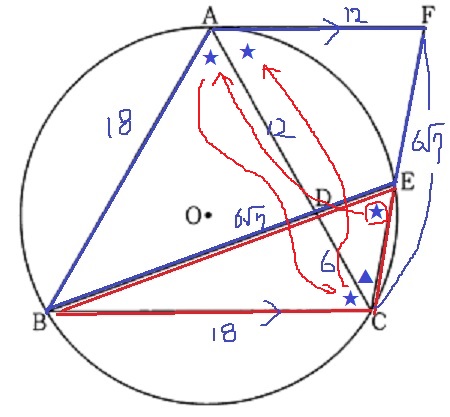
★は全て60°（∠ＣＥＢ→円周角∠ＣＡＢ→正三角形∠ＡＣＢ→錯角∠ＣＡＦ）。
△ＣＤＥ∽△ＣＦＡから、ＣＥ＝１８/７・√７と算出できる。

＠別解２＠

△ＡＢＤ∽△ＥＣＤ
辺の比は、ＢＤ：ＣＤ＝６√7：6＝√７：１
面積比は２乗なので、△ＡＢＤ＝⑦、△ＥＣＤ＝①
（１）の合同から△ＡＣＦ＝⑦
四角形ＡＤＥＦ＝⑦－①＝⑥
ＡＤ：ＤＣ＝２：１より、
△ＢＣＤ＝⑦÷２＝○3.5
したがって、四角形ＡＢＥＦ：△ＢＣＥ
＝⑦＋⑥：○3.5＋①＝２６：９

大問６（規則）

（１）
一番上をとって、２枚目を一番下にする。
問題で聞かれるのは一番上か一番下のカードなので、中は考えない。
Ⅱ図を一番上をみると、１・３・５・７…と奇数の数列となっている。
つまり、最初は奇数だけを取っていき、偶数を残す。

「ｍ＝８」＝８枚のカード。
カードは４枚残すので、４枚取ることになる。
奇数を順番に取ると、４枚目は７。
７を取って、次の８を一番下におく。
すると、一番上に２が現れる。
一番上…２、一番下…８

（２）
３１枚で１６枚を残すから、カードは１５枚取る。

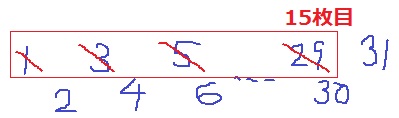
１５枚目は２９のカードになる。
理由は〔１・２〕〔３・４〕…と組で考え、
３０÷２＝１５→〔２９・３０〕の組合せは１５組目となるから。
２９をとって３０を一番下に持ってくると、３１が表れる。
一番上…３１、一番下…３０

（３）
２９４枚で７３枚を残すから、カードは２２１枚を取る。

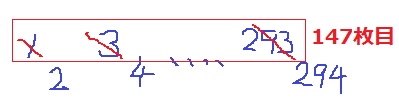
同じように、奇数だけ除外。
奇数&偶数の組は、２９４÷２＝１４７
残り、２２１－１４７＝７４枚のカードを取る。

２からスタートして、最後は２９４。
偶数だらけのなかで、４の倍数でないものを控除する。
気を付けるべき点は、２９４は４の倍数ではないということ。
〔２、４〕〔６、８〕･･･〔290、292〕
うしろの数字を÷４すれば、何組目かがでてくる。
２９２÷４＝７３組目
２９０が７３枚目のカード。７４枚目は２９４。
現れた４を最後にまわす。その次の８が一番上になる。
一番上…８、一番下…４
丁寧な思考過程が求められる。
公立高校入試解説ページに戻る