2018年度　東京都立高校入試【数学】解説

平均６６．５点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）-87.8％

（１）　94.6％
５－１/３×（－９）
＝５＋３＝８

（２）　92.3％
８（ａ＋ｂ）－（４ａ－ｂ）
＝８ａ＋８ｂ－４ａ＋ｂ＝４ａ＋９ｂ

（３）　80.2％
（√７＋２√３）（√７－２√３）　←（ａ＋ｂ）（ａ－ｂ）＝ａ²－ｂ²を利用
＝（√７）²－（２√３）²
＝７－１２＝－５

（４）　88.4％
一次方程式
４ｘ－５＝ｘ－６
３ｘ＝－１　　ｘ＝－１/３

（５）　92.4％
連立方程式
７ｘ－ｙ＝８・・①　　－９ｘ＋４ｙ＝６・・②
①より、ｙ＝７ｘ－８
②に放り込み（ここでは代入法）
－９ｘ＋４（７ｘ－８）＝６
１９ｘ＝３８　　ｘ＝２
①に放り込み。ｙ＝７×２－８＝６
ｘ＝２、ｙ＝６

（６）　91.3％
二次方程式
ｘ²＋１２ｘ＋３５＝０
（ｘ＋７）（ｘ＋５）＝０
ｘ＝－７、－５

（７）　80.1％
１８℃以上の日数は、５＋９＋４＝１８日
１８/４０→４５/１００→４５％

（８）　87.2％
真ん中に３本目の平行線をひいて錯角。

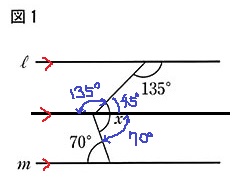
１８０－１３５＝４５°
ｘ＝４５＋７０＝１１５°

（９）　83.2％
*折り返して点が重なるということは、点からの距離が等しい線で折る。
つまり、線分ＰＱの垂直二等分線。

大問２（整数の証明）-35.8％

（１）イ　35.7％
*Ｍは正六角形の中心。Ｎはその１辺の中点。
ａ、ｂ、ｈを使って、正六角柱の表面積を求める。
底面積（上下）・・〔ａ×ｂ×１/２×６×２〕（正六角形の面積は△ＡＢＭ×６）
側面積・・〔ａ×ｈ×６〕
Ｐ＝ａ×ｂ×１/２×６×２＋ａ×ｈ×６
＝６ａ（ｂ＋ｈ）　←６ａでまとめる。
よって、イ：ｂ＋ｈ
（ＭＮさえわかれば、簡単に表面積が求められますね）

（２）公式解答参照　35.9％
*まずはℓをつかわず、ｒとｈだけで表面積Ｑを出してみる。
その後、ℓ＝２πｒを指摘し、ℓ（ｈ＋ｒ）に２πｒ代入。
２つの式がともに２πｒｈ＋２πｒ²で同じ値なので、
Ｑ＝ℓ（ｈ＋ｒ）が導かれる。
(1)六角柱も（２）円柱も、底面積の周り×（中心からの距離＋高さ）ですね。

大問３（関数）-56.1％

（１）ウ　85.3％
*Ｐはｙ＝１/２x²のグラフ上でＡとＢの間。
すなわち、－４≦ｘ≦６のときのｙ変域を考えればいい。
ｘ＝０のとき　最小値ｙ＝０
ｘ＝６のとき　最大値ｙ＝１８
よって、ウ：０≦ｂ≦１８

（２）①ア　74.9％
*点Ｐは原点にある。
ＭはＰ（０、０）とＱ（０、１２）との中点なので、Ｍ（０、６）
Ｍ（０、６）→Ｂ（６、１８）は、右に６いって上に１２なので、傾きは１２/６＝２
切片は６だから、ア：ｙ＝２ｘ＋６

②（４、８）　8.2％!!
*おなじみのやり方。
求める点Ｐのｘ座標をｔとおく→Ｐ（ｔ、１/２t²）
ＱとＭのｘ座標もｔ。これらのｙ座標もｔで表す。
直線ＡＢ。Ａ→Ｂで、右に１０、上に１０だから傾き１。
切片は１２（ＡとＢを定規で結んでもＯＫ）
ｙ＝ｘ＋１２　　→　Ｑ（ｔ、ｔ＋１２）
直線ＯＢ。Ｏ→Ｂで、右に６、上に１８だから、
ｙ＝３ｘ　→　Ｍ（ｔ、３ｔ）

ＱＭＰのｙ座標で、Ｑ－Ｍ＝Ｍ－Ｐとなるから、
ｔ＋１２－３ｔ＝３ｔ－１/２t²
１/２t²－５ｔ＋１２＝０
（ｔ－４）（ｔ－６）＝０
問題文より、－４＜ｔ＜６なので、
ｔ＝４　→ＰＭＱのｘ座標は４
これをｙ＝１/２x²の式に代入して、Ｐ（４、８）

大問４（平面図形）-52.6％

（１）エ　62.6％
ＢＣに補助線。
円周角定理により、半円の弧に対する円周角は直角なので、∠ＡＣＢ＝９０°
弧ＡＣ＝弧ＢＣだから、ＡＣ＝ＣＢ（弦も等しい）
すると、△ＡＣＢは直角二等辺三角形であり、∠ＣＡＢ＝４５°
△ＡＣＱで外角定理→∠ＡＱＰ＝ａ＋４５

（２）①公式解答参照　76.1％
△ＡＢＰと△ＡＲＰにおいて、
ＢＰ＝ＲＰ
ＡＰは共通辺
円周角定理により、∠ＡＰＢ＝９０°
∠ＡＰＲも９０°
２辺とあいだの角が等しい→合同！

②２/３倍　19.2％！
相似図形がいっぱいあって迷いやすい。

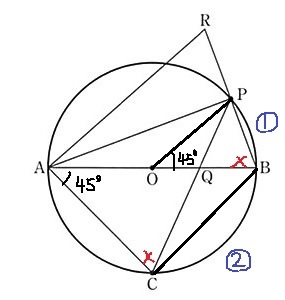
初期図。
四角形ＡＯＰＲなので、ＯＰに線をひいて形をつくる。

ついでにＣＢにも線をひく。
△ＡＣＢは直角二等辺三角形なので、∠ＣＡＱ（ＣＡＢ）＝４５°
弧BCの中心角である∠COBが垂直なので、弧PBの中心角∠BOP＝４５°
∠CAQ＝∠BOP（＝４５°）

また、弧ＡＰに対する円周角より、∠ＡＣＱ＝∠ＯＢＰ
２角が等しいことから、△ＡＣＱ∽△ＯＢＰ

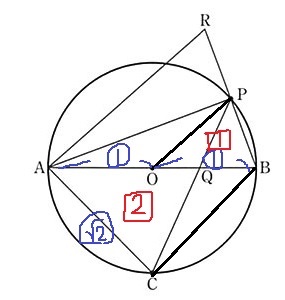
半径をＯＢを①とおき、辺の比から△ACQと△OBPの面積比を調べる。
△ＡＣＢは直角二等辺三角形だから、三平方からＡＣ＝○√２とわかる。
面積比は辺の比の２乗
△ＡＣＱ＝□２　△ＯＢＰ＝□１

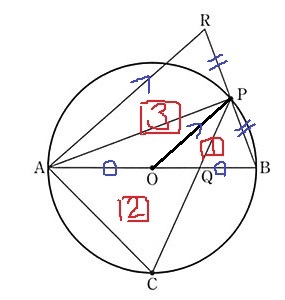
△ＡＢＲ内で中点連結定理。
△OBP＝□１より、四角形ＡＯＰＲ＝□３となり、２/３倍

ACBの直角三角形を利用して、△ＡＣＱ∽△ＯＢＰをみつけたい。
そこまでたどり着ければ、BCはいらない。
△ACQと△OBPの面積比がでて、
△OBPから中点連結定理より四角形AOPRの面積比もでる。

大問５（空間図形）-17.6％

（１）６０°　20.6％！
*立体内部の図形の角度は、その図形がどんな形か着目してみよう。
ＰがＣにあるので、△ＢＤＣに注目！
どの辺も９ｃｍ×９ｃｍの正方形の対角線。
つまり、３辺が等しいので正三角形→∠ＢＰＤ＝６０°

（２）８１ｃｍ³　14.6％！
*底辺を△ABDにして考える。
高さを求めればおしまい。

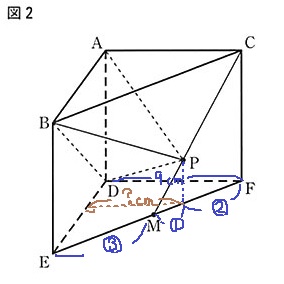
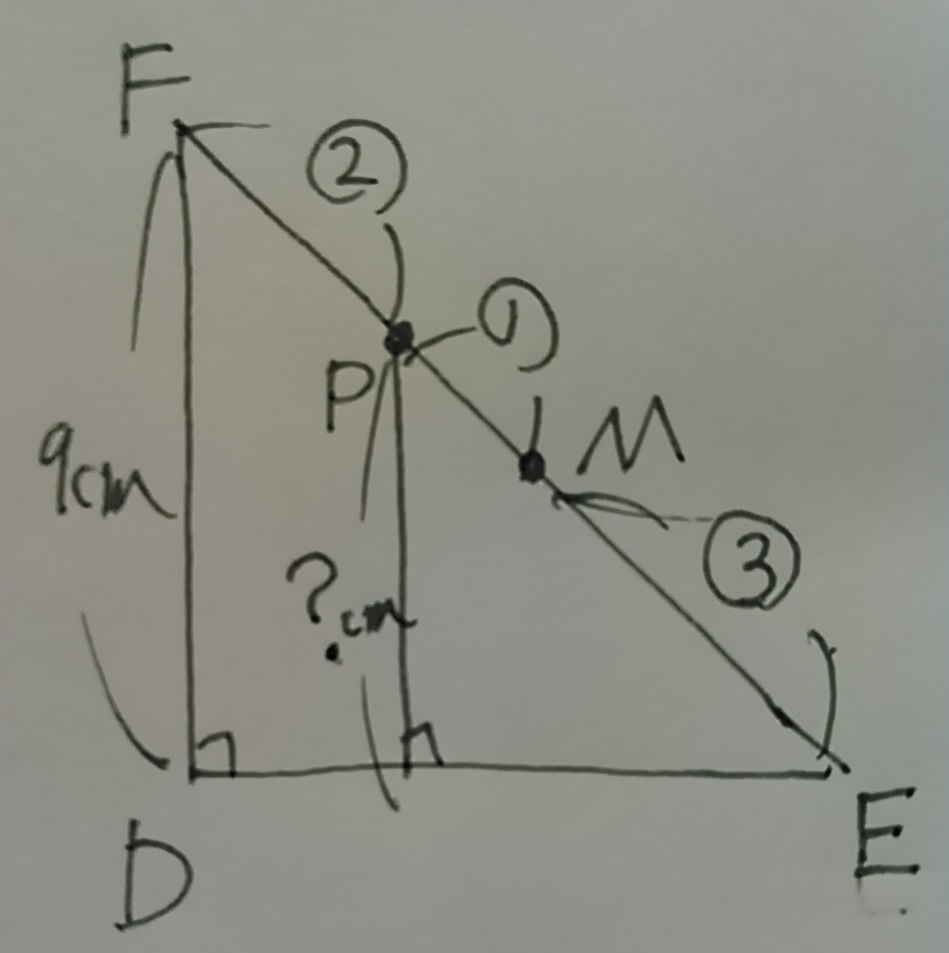
高さは△FDE方向。（Ｐは辺ＥＦ上へ垂直におろす）
FE上の辺の比から、
？＝９×４/６＝６ｃｍ
したがって、９×９×１/２×６×１/３＝８１ｃｍ³
公立高校入試解説ページに戻る