平均23.1点（前年比；－3.4点）
問題はコチラ→ＰＤＦファイル
大問１（計算）
（１）
３－（－４）
＝３＋４
＝７
（２）
４（ｘ－２ｙ）＋３（ｘ＋３ｙ－１）
＝４ｘ－８ｙ＋３ｘ＋９ｙ－３
＝７ｘ＋ｙ－３
（３）
15/８ｘ2ｙ÷（－５/６ｘ）
＝－９/４ｘｙ
（４）
（√６－２）（√６＋３）－４√３/√２
＝（６＋√６－６）－４√６/２
＝√６－２√６
＝－√６
（５）
（３ｘ＋１）（ｘ－４）－（ｘ－３）2
＝３ｘ2－11ｘ－４－（ｘ2－６ｘ＋９）
＝３ｘ2－11ｘ－４－ｘ2＋６ｘ－９
＝２ｘ2－５ｘ－13
大問２（小問集合）
（１）
４ｘ2－９ｙ2
＝（２ｘ＋３ｙ）（２ｘ－３ｙ）
（２）
Ｖ＝１/３Ｓｈ ←両辺３倍で左右入れ替え
Ｓｈ＝３Ｖ ←÷Ｓ
ｈ＝３Ｖ/Ｓ
（３）
ア：絶対値とは数直線上で原点０からの距離。３の絶対値は±３。×
イ：自然数は１、２、３、４…といった正の整数。
ｍ≦ｎのとき、ｍ－ｎは０か負の数だから自然数ではない。×
ウ：√25＝√５×
25の平方根は±５（２乗して25になる数）
エ：有理数とは整数の分数で表せる数。〇
エ
（４）
全体は６×６＝36通り
●和が５→（１、４）（２、３）と逆を含めた４通り
●和が10→（４、６）（５、５）（６、４）の３通り
計７通りだから、確率は７/36。
（５）
体積比は相似比の３乗。
Ａ：Ｂ＝２3：５3＝８：125
体積８のＡを使い、体積125のＢを満水にする。
125÷８＝15回…５
16回目で満水に達する。
（６）
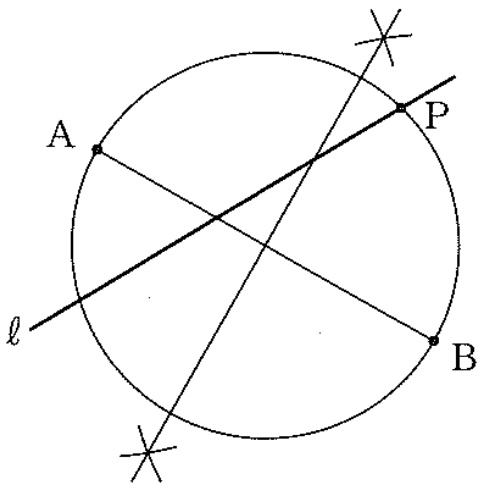
ＡＢを直径とする円を描くと、直径に対する円周角で∠ＡＰＢ＝90°
①ＡＢの垂直二等分線
②ＡＢの中点に針を合わせ、Ａまでの距離（半径）をとって円を描く。
③直線ℓとの２つの交点のうち、１つにＰを記す。
（７）
答案では文字が何を表すか最初に書いてから方程式をつくり、答えを求める過程も記述する。
最も小さい自然数をｘとすると、連続する３つの自然数はｘ、ｘ＋１、ｘ＋２。
ｘ2＋（ｘ＋１）2＝10（ｘ＋２）＋５
ｘ2＋ｘ2＋２ｘ＋１＝10ｘ＋20＋５
２ｘ2－８ｘ－24＝０ ←÷２
ｘ2－４ｘ－12
＝（ｘ＋２）（ｘ－６）＝０
ｘ＝－２、６
ｘは自然数なのでｘ＝６
連続する３つの自然数は６、７、８。
大問３（データの活用＆数量変化）
（１）①
最小値は30～40点→ウ×
最大値は90～100点。
30人の第２四分位数は15番目と16番目の平均で60～70点。
第１四分位数は下位15人のうち下から８番目で50～60点→エ×
第３四分位数は上位15人のうち上から８番目で70～80点→ア×
イ
②
１：四分位範囲＝第３四分位数－第１四分位数
箱の横の長さで３組の方が大きい。×
２：45点はいずれの組も第１四分位数より下。
最小値から45点以下が１人ずついるのは確定だが、それ以上はわからない。△
１…イ ２…ウ
（２）①
学校～公園までの時間は、1200÷80＝15分
午前９時15分
②
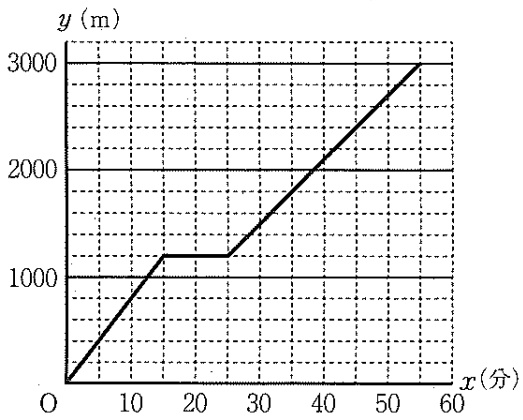
スタートから15分後に公園へ到着。10分間休憩。
公園～図書館は、1800÷60＝30分
９時55分に図書館へ到着する。
③
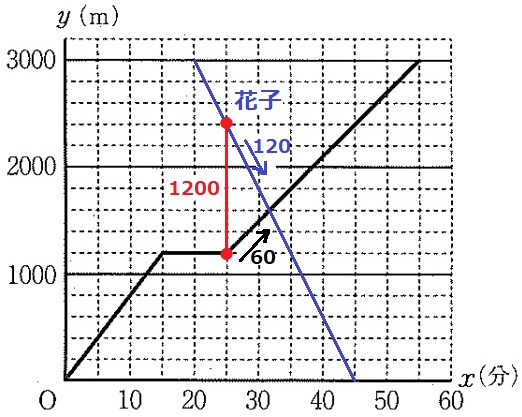
花子のグラフを記入。
太郎の速さは分速60ｍ、花子の速さは3000÷25＝分速120ｍ
格子点に着目すると太郎が公園を出発したｘ＝25のとき、花子との距離は1200ｍ。
１分ごとに120＋60＝180ｍずつ近づくので、1200÷180＝６・２/３分＝６分40秒後に出会う。
９時25分から６分40秒後の午前９時31分40秒。
大問４（関数）
（１）
ｙ＝１/２ｘ＋３にｘの値を代入する。
ｘ＝－２のとき、ｙ＝２
ｘ＝３のとき、ｙ＝９/２
２≦ｙ≦９/２
（２）
Ａ（－２、２）をｙ＝ａｘ2に代入。
２＝４ａ
ａ＝１/２
（３）①
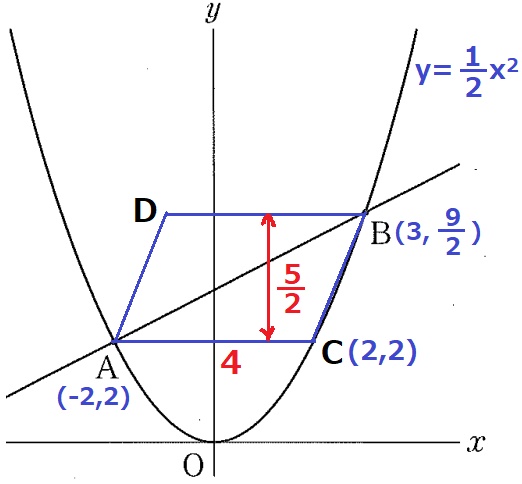
ＡＣとｘ軸が平行→放物線上にあるＡとＣはｙ軸について対称→Ｃ（２、２）
平行四辺形ＡＢＣＤの底辺ＡＣ＝４、高さは９/２－２＝５/２
平行四辺形の面積は、４×５/２＝10
②
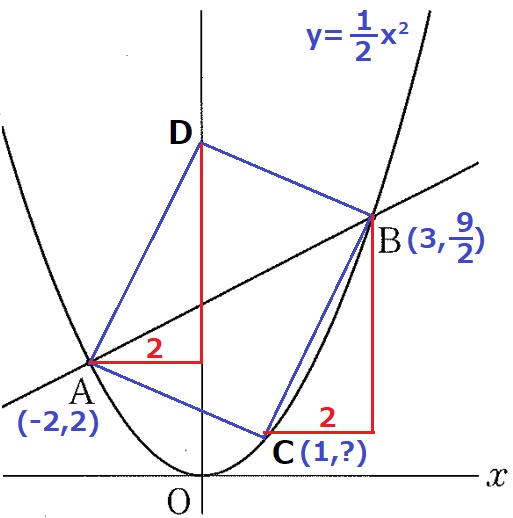
ＡとＤのｘ座標の差は２→ＣとＢのｘ座標の差も２。
Ｃのｘ座標は、３－２＝１
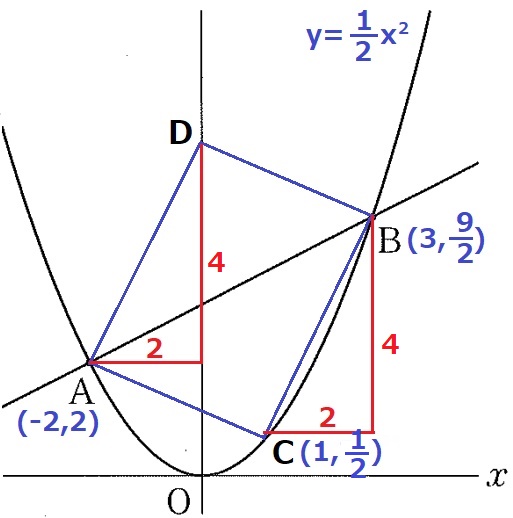
ｙ＝１/２ｘ2にｘ＝１を代入して、Ｃのｙ座標は１/２。
ＢとＣのｙ座標の差は、９/２－１/２＝４
ＤとＡのｙ座標の差も４だから、Ｄのｙ座標は２＋４＝６
大問５（平面図形）
（１）
△ＡＣＧ≡△ＡＤＥの証明。
仮定のＡＢ＝ＡＣ、ＡＢ＝ＡＤから、ＡＣ＝ＡＤ
共通角で∠ＣＡＧ＝∠ＤＡＥ
弧ＡＦの円周角＋二等辺ＡＢＤの底角で∠ＡＣＧ＝∠ＡＤＥ
１辺と両端角が等しいから△ＡＣＧ≡△ＡＤＥ
（２）①
前問の合同より、対応する辺は等しいのでＡＧ＝ＡＥ＝４ｃｍ
ＥＣ＝６－４＝２ｃｍ
ＡＤ//ＢＣ→２角相等で△ＡＥＤ∽ＣＥＢ。
ＢＣ＝６×２/４＝３ｃｍ
②
面積を出すにはどこかで直角をつくる必要がある。
△ＡＢＣは二等辺三角形。ＡからＢＣに垂線をひいた足をＨとするとＡＨ⊥ＢＣ。
△ＡＨＣで三平方→ＡＨ＝３√15/２ｃｍ
Ｆを通る直線ℓに平行な線をひき、ＡＨとの交点をＩとする。
ＡＩが△ＤＧＦの高さにあたる。
２角相等で△ＤＧＦ∽ＢＣＦより、ＧＦ：ＦＣ＝２：３
→ＡＧ//ＩＦ//ＢＣから、ＡＩ：ＩＨ＝②：③
△ＤＧＦの面積は、２×（３√15/２×②/⑤）÷２＝３√15/５ｃｍ2
平均は下がったが、全体的に難しくはない。
大問１
完答を目指したい。
大問２
ここも完答を目指したい。
（３）ウ：√25という数の根号を外す問題と、25の平方根を問う問題は別。
（６）条件を満たす点は２つあるが１つで良かった。
（７）最も小さい数をｘとすると、連続する３つの自然数はｘ、ｘ＋１、ｘ＋２。
問題文通りに立式できれば、あとは計算するのみ。
大問３
（２）算数の範囲で解ける。正解したい。
大問４
（３）①図１に作図してみよう。Ｃ座標がわかれば平行四辺形の底辺と高さがわかる。
②公立入試の世界でよく見かける。対辺が平行で長さが等しい平方四辺形の特徴を使う。
大問５
（２）①ＢＣを１辺とする三角形と相似にある三角形を探す。
ＡＤ//ＢＣが見つけやすい。
②底辺はＧＤ＝２ｃｍ、高さを求めるには垂直をどこで使うか。
円の中心Ｏは通らない→円周角は使えない。
二等辺三角形ＡＢＣを二つに割る垂線に着目する。
ＡＤとＢＣの距離が出る。ＡＤからＦまでの距離に分けるにはどこの比を見るべきか。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント