平均41.7点(前年比;-2.3点)
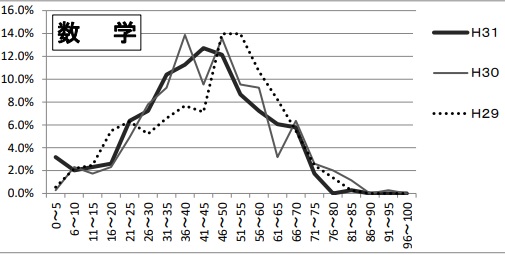
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 95.4%
-2a+5a
=3a
(2) 93.1%
(-8)÷(-4)-1
=2-1
=1
(3) 67.9%
3x2÷(-y2)×2xy3
=-63y
(4) 85.5%
10/√5-√45
=2√5-3√5
=-√5
(5) 89.9%
x2+6x-27
=(x+9)(x-3)
(6) 85.3%
連立方程式。①の式を②に代入すると、
x-2(5-3x)=4
x-10+6x=4
7x=14
x=2
①に代入、y=5-3×2=-1
(7) 80.6%
因数分解ができないので解の公式を適用。
x={-(-3)±√(-3)2-4・2・(-1)]/(2・2)
=(3±√17)/4
(8) 53.8%
傾きは、右に6、上に3→1/2
あとは、y=1/2x+bに放り込んで切片を求める。
0=1/2×(-2)+b
b=1
y=1/2x+1
(9) 67.3%
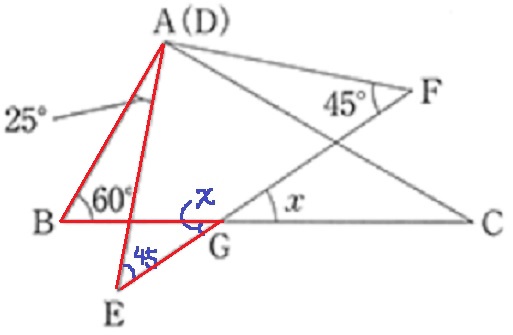
↑ここに着目する。
こういう蝶々型は先端の角の和が等しい(対頂角で相殺できるから)
25+60=x+45
x=40°
(10) 46.8%(一部正答17.1%)
関数の正誤判定。
ア:代入してみると×!
イ:左右対称なのでy軸について対称○
ウ:最小値はx=0のとき、y=0。y=ax2のグラフは原点を通る。
y変域は0≦y≦4。×!
エ:(42-22)/(4-2)=6○
y=ax2のグラフにおいて、p→qの変化の割合はa(p+q)だから、
1(2+4)=6でもいける。
オ:xが減るとyも増加。×!
(11)① 32.1%!
赤い布をx枚使ったとする。
最初の布は50cm。2枚目以降は縫い目を引いた45cmずつ増えていく。
合計で500cmになればいい。
50+45(n-1)=500
x=11 →11枚
〔全体の長さ-縫い目の合計=500〕でも可。
50n-5(n-1)=500
n=11 同じだね!(p_-)
② 0.6%!!!(一部正答3.2%、無答54.9%!)
記述式。
公式解答ではいきなり45x+25y+5=500とある。
これは、つなぎ目分の5cmを初めにカウントしておいて、
それ以降は赤を1枚たすと45cm、白を1枚たすと25cmのびるから。
45x+25y+5=500
45x+25y=495
9x+5y=99
式が1つしかない。いわゆる不定方程式で地道に代入する。
赤の布は500÷50=10で白い布も使うから、0<x<10となる。
(x、y)=(1、18)(6、9)
不定方程式の攻略が厄介。
コツとしては、x=1をいれると、5y=90とキリ良くなるので、
つぎに5の倍数をつくるには、xに1+5=6を代入する。
@公式解答の別解より@
45x+25y+5=500をxについて解き、
x=11-5/9y
xは自然数なので、yは9倍数でなければならない。
(x、y)=(1、18)(6、9)
大問2(小問集合)
(1) 27.7%!
標本調査。
30個の抽出で、白:オレンジ=24:6=4:1
この割合は母集団も変わらないとする。
最初の白は、50×4/1=200個
(2) 10.4%!
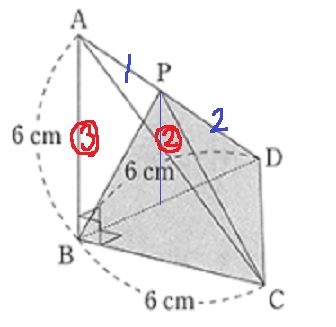
これが見えたらしめたもの。
6×6×1/2×(6×2/3)×1/3=24cm3
(3) 21.4%!(一部正答16.2%)
105°の作図。
105=45+60
公式解答では、Aを通る直線ABの垂線をひき、その2等分線を作成(45)
左側に正三角形をつくって60を足す。
コンパスでつくりやすい角度は垂直の90°、正三角形の60°
これらの二等分線で45°と30°
4つをうまく組合せて105を作る。
遠回りだが、75(=60+30÷2など)を作って105(=180-75)もできる。
(4) 9.8%!!(一部正答30.3%)
平行四辺形の証明。
平行四辺形であるための5つの条件を覚えているかな?

問題集で見かけた人もいると思う。
使うべきは『対角線が各々の中点で交わる』
★-〇=△を丁寧に記述すること!
大問3(関数)
(1) 45.4%
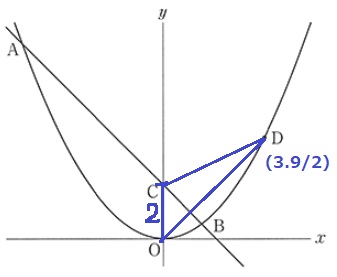
2×3×1/2=3cm2
Dのy座標いらなかった。
(2) 2.0%!!
△ADC:△CDB=4:1
AC:CB=4:1
このあとが手詰まる。
AとBはy=1/2x2とy=ax+2の交点にある。
Bのx座標をsとおいて座標をだす。
Aのx座標は-4s

ここからy座標をいじる。
2つのグラフの交点からy座標で等式を作る。
〔A〕
8s2=-4sa+2
8s2+4sa-2=0…①
〔B〕
1/2s2=sa+2
s2-2sa-4=0…②
連立方程式の要領で①-②×2
8s2+4as-2=0
+)2s2-4as-8=0
10s2 -10=0
s=1
B(1、1/2)
C→Bは右に1、下に3/2
傾きa=-3/2
@公式解答より@
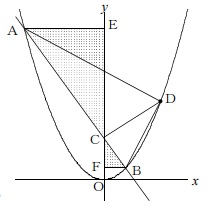
△ADC:△CDB=4:1
AC:CB=4:1
上のような補助線をひいて、E、Fをつくる。
△ACE∽△BCF
EC:CF=4:1
Bのx座標をtとすると、Aのx座標が-4t
E(0、8t2) F(0、1/2t2)
EC(8t2-2):CF(2-1/2t2)=4:1
t=±1
t>0より、t=1
A(-4、8)となり、a=-3/2
大問4(平面図形)
(1) 35.3%
半円の弧に対する円周角APBは90°
∠ABP=60°なので、
△PABは〔30°-60°-90°〕→1:2:√3の直角三角形
AP=6×√3/2=3√3
PM=3√3×1/3=√3cm
(2)① 0.3%!!!
記述式。
BQを折り目としてPとOが重なるということは、
BQを対称の軸として線対称の関係にある。
これを示すには△OBPに注目する。以下、公式解答を参考。

∠PBO=60°と半径を手がかりに△OBPは正三角形。
△PBMは前問よりPM=√3、BP=3、∠BPM=90°
△PBMは1:2:√3の直角三角形。
∠PBM=30°
∠PBO=60°なので、QBは∠PBOの二等分線となり、
△OBPは正三角形だから、底辺であるOPを垂直に二等分する。
公式解答の文章は飛び飛びな印象がある。どの程度の指摘で足りるのか迷うが厳密性は緩い。
② 0.3%!!!
ラストの求積。幾何的な発想力が求められる。
実は正三角形が3つある。

なんとなくMがOの真上にあるのでは?と感じた人もいたと思う。
AQとQOをひく。
△OBQは半径から二等辺。ORは底辺BQを垂直に二等分する。
△ORQは30°-60°-90°の直角三角形。
これをもとに角度を調べていくと、△AOQも△OPQも正三角形になる。
図形全体が線対称で、QP//ABとなる。

等積変形で△OQP=△BQPとなる。

四角形QOPM(赤)=△QOP-△QMP
△MBP(黄)=△QBP-△QMP
△QOPと△QBPから、共通する△QMPをひくので、
四角形QOPM=△MBPとなる。
求積すべき図形は、60°の扇型から△MBP(黄)をひけばいい。

3×3×π×1/6-3×√3×1/2
=3/2π-3/2・√3cm2
@別解@

まとめて等積変形しなくても、四角形QOBPは平行四辺形で、
Rは対角線OPとQBの中点だから、△QORと△BPRは合同。
ここから左の面積を右に移して、△MBPとしてもいい。
@別解2@

移動させなくても分割で攻略もできる。
Mは正三角形QOPの重心にあるので、△QMPは正三角形の3分の1。
扇型から正三角形の3分の2を引けばいい。
@余談@
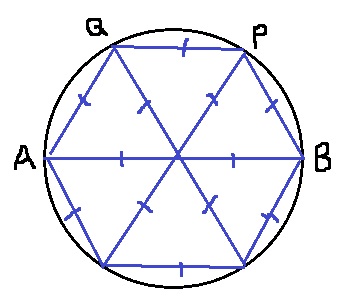
正六角形の分割。
中学受験では馴染みのある図形で、覚えておくと便利。
弧QPは円周の6分の1で、弦QPは直径と平行かつ半分の長さになる。
サボの解法はこれがもとになっています。
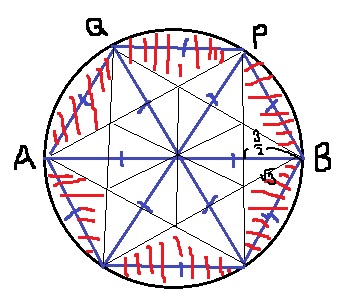
さらにいじってみると、一辺が√3の正三角形が12個できる。
3×3×π(円)-√3×3/2×1/2×12(中のヤツ)
=9π-9√3
これを6で割る。
(9π-9√3)÷6=3/2π-3/2・√3cm2
@公式解答より@

2019年度(埼玉)
社会…平均59.3点 理科…平均43.8点 英語…平均47.1点
その他は下記リンクの目次からどうぞです。



コメント
わかりやすい解説ありがとうございます????
ありがとうございます(^^)
今年度の埼玉は英理社を掲載予定ですが、少々遅れるかもしれません。
直前期までには終わらせます。