大問1(計算)
(1)
(-7)+15
=-7+15
=8
(2)
8-(-5)2 ÷5/2
=8-25×2/5
=-2
(3)
1/2(4a+8b)-3(a-b)
=2a+4b-3a+3b ←符号注意!
=-a+7b
(4)
一次関数の一般式は、y=ax+b
点(1、3)を通る → x=1のときy=3
傾き-2 → a=-2
3=-2×1+b
3=-2+b
b=5
y=-2x+5
(5)
(√3+2)(2√3-1)
=6-√3+4√3-2
=4+3√3
(6)
2x2-7x+4=0
解の公式。
x=(7±√17) /4
ちなみに、平方完成で解くと・・
2x2-7x+4=0
x2-7/2x+2=0 ←両辺を÷2
x2-7/2x=-2
(x-7/4)2-49/16=-2 ←7/4の2乗が49/16なので
(x-7/4)2=17/16
x-7/4=±√17/4
x=(7±√17)/4
大問2(小問集合)
(1)
チーバくん、高校入試にあらわる!いつもツイッター見てるよ(σ・д・)σ
面積比は相似比の2乗。
チーバくんは複雑な形をしていますが、上の定理は使えます。
相似比は3:5なので、面積比は3×3:5×5=9:25
ウ
(2)
いろんな解き方があるかと思います。
円が描かれていることから、円周角の定理をフル活用して、
判明した角度をどんどん図に書き込んでみましょう。
以下、最短ルートと思われる解法です。
対頂角から、∠DOC=48°
弧DCに着目し、∠DECは∠DOCの円周角であることから24°
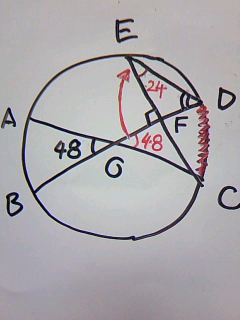
BDとECの交点をFとして、△EFD上の外角定理から、
∠ODE=90-24=66°
(3)
回転図形は、底面積が必ず円になります。
イメージ図↓

ホールケーキのような形になります。
イメージに成功できれば、正解したようなものです。
計算するときは、赤い部分の表面積を半径4cmの円と考え、
一括処理します。
4×4×π×2+4×2×π×2+2×2×π×2
=32π+16π+8π=56πcm3
(4)
問題:√(50-2n)/3が自然数になるとき、自然数nの値を求める。
一行問題だけど、正解率は低い:;(∩´﹏`∩);:
自然数は、1、2、3、4、5…と続く数の総称。
√(50-2n)/3が自然数であるということは、
分子の√(50-2n)が根号を外せる形でないといけません。
根号付きの数を3で割っても自然数にはなりませんからね(無理数になる)
根号を外せる形とは、根号の中が1、4、9、16・・・といった平方数。
①:50-2nが平方数。(=√を外せる)
②:50-2nが3で割り切れる。
③:nが自然数。
nに1、2、3・・を代入して、地道に調べる方法もありますが、
50-2nがどんな平方数になるかを調べた方が早いです。
①より、50-2nの平方数として候補にあがるのは、
1、4、9、16、25、36、49のみ。
64だと50を超えてしまいます。
nが負の数も含めれば50-2nの値は50を超えますが、
nも自然数なので50-2nの値は50未満になります。
②より、50-2が3で割り切れる場合は、
先ほどの候補から3の倍数である、√9=3 or √36=6
③より、√9だと、50-2n=9 n=20.5となり、
nが自然数ではなくなるので×。
√36だと、50-2n=36 n=7となり、nも自然数となります。
答えは7
(5)
値の大きくなるbから考える。
b=1 3b =3 a=1、2、3、4、5
b=2 3b =9 a=1、2、3
b=3 3b =27 a=1
計9通り
サイコロの出目は6×6=36通り
確率は9/36=1/4
(6)
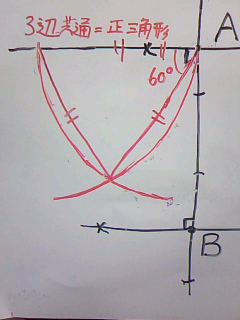
点Aを頂点、点Bが底辺の中点になるように正三角形を書きます。
単純そうに見えますが、簡単ではないと思われます。
最初の突破口は、正三角形の性質のなかで何が使えるのかを見つけることです。
正三角形の真ん中の芯から、両サイドの頂点を作図するにはどうすれば良いでしょうか?
正解は、正三角形の底辺を垂直に二等分する線は頂点を通ること。
この逆も真で、頂点と底辺の中点を通る線(本問でいうAB)は底辺(PQ)と垂直に交わります。
そこで、点Bを通るABと垂直な線を書きます。
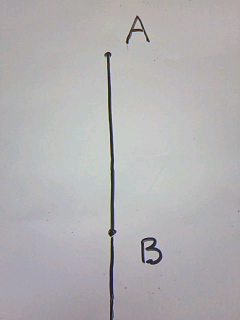
まずは半直線ABをひいて・・
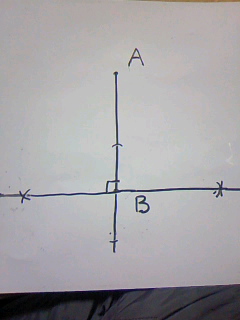
こんな感じに。
この線上のどこかにP、Qが潜んでいるわけです。
ここから悩んだ受験生、多かったと思います。
PB=QB、AP=AQから辺で攻めようとしても、
どの辺の長さもわからず八方塞に・・・。
そこで角度から攻めます。
正三角形を縦に割ったとき、半分になった三角形は、
直角、60°、30°の直角三角形になります。
頂点AからABと30°になる線をひければ、
先ほどのひいた線と交わるところが底角になります。
30°をつくりたいわけですが、いきなりは作れません:(っ`ω´c):
いったん60°を作成して、それを二等分する手法をとります。
1つ作業をはさまなくてはならないのですね。
そして、60°の作成といえば正三角形です。
ABを1辺とする正三角形を画きます。
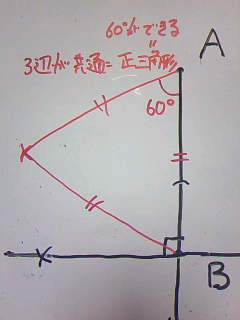
ABの長さをとって、AとBからヒョコ、ヒョコを印をつけます。

ここから、角の二等分線。
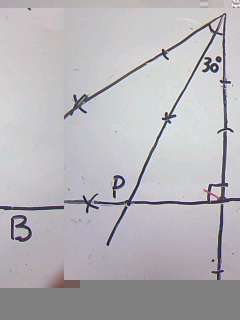
(画像がバグってる!左のBは気にしないでください)
交わった点がPです。
あとは、APの長さをとって、それを反対側にもっていけばQ誕生。
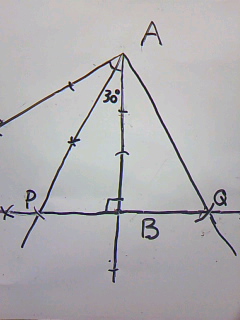
完成! ものすごいいびつな正三角形になってしまいました・・
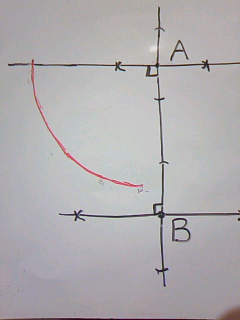
<別解>
公式の正解表にある別解の解説です。
基本的には、上と同じ考えを用います。
まずは、BだけでなくAについても垂線をひきます。
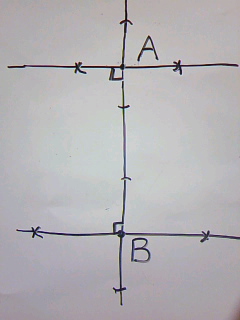
ここで、ABから30°の線をひくのですが、
60°製作のために画く正三角形を外側におきます。
つまり、上は60÷2=30でしたが、今度は90-60=30です。
Aから適当な長さをとって・・・
交点から同じ長さでグルっと線を・・

その交点とAを結べば、∠BAP=30°になります。
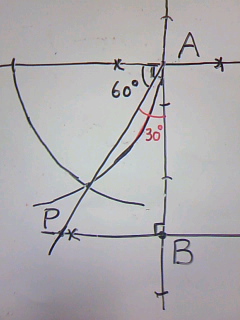
あとは、APの長さを反対にもってきてQをつくれば完成!
大問3(文章題)
(1)
標本調査に関する問題です。
標本調査とは、例えばテレビの視聴率のように全ての受信機(テレビ)を調べるのが困難な場合、
アットランダムで抽出した一部の標本を調査し、
その中での傾向から全体(母集団)を推測する統計手法です。
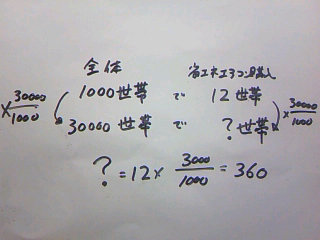
(1)・・・360
1000:12=30000: ? と比で解いてもOKです。
後半は、連立方程式の問題であることに気づけば、あとは計算をするだけです。
LED電球をx個、白熱電球をy個とおき、値段と消費電力で2つの式を立てます。
3000x+100y=122000 ・・A
10x+60y=1600 ・・B
受験生に人気なのは加減法だと思いますが、ここでは代入法で解いてみます。
Bを÷10して、
x+6y=160
x=160-6y
Aに代入
3000(160-6y)+100y=122000
480000ー18000y+100y=122000
17900y=358000
y=20
x=160-6×20=160-120=40
LED電球が40個、白熱電球が20個。
(2)・・・40 (3)・・・20
ケタが多いので、ケアレスに注意してくださいね!
(2)
1つずつ丁寧に処理していきます。
1ヶ月の使用時間が200時間で、LED電球の寿命が40000時間なので、
40000÷200=200ヶ月 ( 4 )・・・200
総費用yは、電気料金と値段をあわせたものです。
y= ( 5 ) x+3000のうち、
3000がLED電球の値段で、( 5 )xが電気料金です。
初期コストの3000円で固定費で、電気料金は使用時間に応じた変動費だからです。
xは月ベースなので、1ヶ月あたりの電気使用量は、
0.23円(1時間あたりの電気料金)×200時間=46円 (5)・・・46
(5)と同様に、y=変動費の電気料金+固定費だから、
y=1.38×200x+100=276x+100 (6)・・・276x+100
白熱電球は5ヶ月で寿命を迎えるので、5<x≦10すなわち5ヶ月~10ヵ月後では
電気料金は変わらないのですが、新しく電球を買うので固定費が+100となります。
y=276x+200 (7)・・・276x+200
(8)が最大の難所:;(∩´﹏`∩);:
LED電球は(5)からy=46x+3000
白熱電球は(6)、(7)からy=276x+100
(ただしxが5増えるたびに+100の条件付)
問題文のグラフにLED電球のグラフを書いて、白熱電球のグラフと交わったx座標が答えなのですが、
y軸に目盛りがないので正確なグラフを画くのは困難かと思います(汗)
とりあえず、 白熱の条件を無視して上の2式の交点をだします。
46x+3000=276x+100
230x=2900
x=2900÷230=12.60・・・
条件なしだと12ヶ月後にLEDの方がお得になるのですが、
条件を考慮すると白熱では5ヶ月ごとに100円加算されるので、
実際、LEDがお得になる時期はもっと早く訪れます。
12ヶ月後では白熱電球を2回取りかえているので+200されますから、
46x+3000=276x+300
230x=2700
x=2700/230=11.73・・・
11ヵ月後にLEDの方が白熱よりお得になる。
(8)・・・11
大問4(関数)
(1)
放物線の式を求める問題ですから、放物線上の点座標に注目します。
y=ax2より、A(4、16a)
EFはCDの2分の1で、y=ax2はy軸を対称軸として左右対称なので、
Fのx座標は2
F(2、4a)
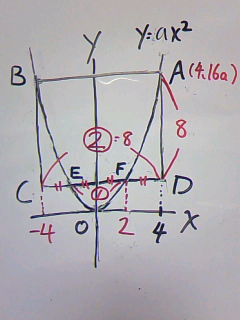
Bのx座標は、Aのx座標と左右対称なので-4
正方形の一辺は長さは、4-(-4)=8
ということは、Aのy座標とFのy座標の差も8なので、
16a-4a=12a=8
a=2/3
(2)
△ABEと△APEの面積が等しくなるときときたら等積変形です。
イメージ図↓
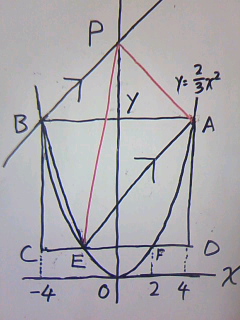
底辺を同じくすれば、頂点をどこに平行移動しても面積は等しくなります。
これは、三角形の面積は、底面×高さ÷2で求まるところ、
底面が同じで、かつ平行線の距離はどこも等しいことから高さも同じなので、
面積も等しくなるからです。
AEを底辺にBをy軸へ平行移動したところが点Pとなります。
そして、点Pを求めるにはBPの式を求めます。
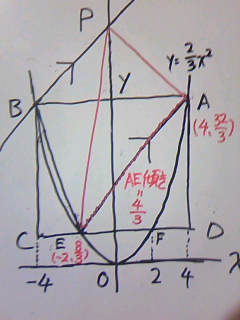
BPの式を求めるには、BPの傾きとB座標が必要です。
B座標は(1)より判明します。
BPの傾きは平行であれば傾きが等しいことから、EAの傾きとなります。
EAの傾きを知るには、AとEの座標が必要です。
(1)より、A(4、32/3)
Eの座標はFと左右対称なのでE(-2、8/3)
2点を通る一次関数の式は連立方程式を利用。
32/3=4a+b
8/3 =-2a+b
6a=8
a=4/3
(*EAの傾きを知りたいので、bは不要)
BPの傾きも4/3
BはAと左右対称なので、B(-4、32/3)
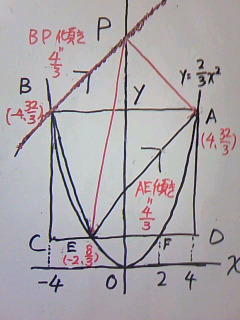
32/3=-4×4/3+b
32/3=-16/3+b
b=16
BPの式は、y=4/3x+16
PはBPの切片なので、P(0、16)
大問5(平面図形)
(1)
AIとBGに印をつけてみます。
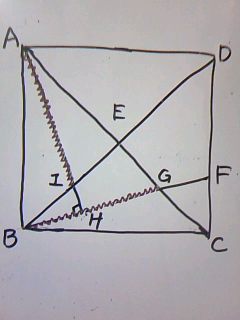
これらが等しいということは、これらを一辺とする三角形が互いに合同であることを
証明すればAI=BGが示されます。cは合同ですね。
問題はどの三角形を選択するかです。
△ABIからでも証明できるのですが、これを選んでしまうと対応する△BCGが
選択肢にないので誤りとなります。
答えは△AIEと△BGEのイ
(2)
普段は、証明の出だしがあらかじめ書かれているのですが、
今年は初めから自力で書き出させる形式となりました。
△AIEと△BGEの各々の辺と角を眺めて、どこが等しくなるのかを考えます。
正方形は、各々の対角線を垂直に2等分しますから、
AE=BE
∠AEI=∠BEG=90°
2辺とその間の角ですとIE=GEを示さなくてはなりませんが、
どちらの辺の長さも不明なので使えません。
そこで、∠EAI=EBGを示して一辺両端角が等しいかを考えます。
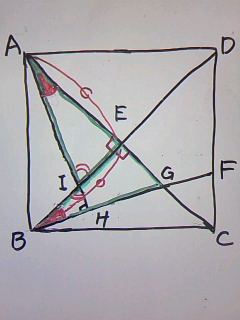
ここで、△AIEと△BIHに注目です。
仮定と正方形の性質から、
∠AEI=∠BHI=90°
対頂角で、
∠AIE=BIH
2つの角が等しいのであれば、残りの角も等しくなるので、
∠EAI=EBG
一辺両端角が等しいことから、
△AIE≡△BGE
AI=BG
(3)
満点を取らせない問題かと思われます。(泣)
この手の問題は、大抵前問を利用するのですが、
△AIEと△BIHにこだわり過ぎると正解にたどりつけません。
視点を変えて、どこが合同か、あるいは相似かを探し出さなくてはなりません。
最終的には正方形の面積を求めたいので、
正方形の1辺か対角線の長さがわかればOKなのですが、
一体、どれが使える図形なのでしょうか。
結論からいえば、△BHI∽△AGHを利用します。
これらは(2)より、2角が等しいので相似になります。
AI=BGなので、AI=2+3=5
そして、IHをxとおくと・・・

△BIH:△AGH=2:x=(5+x):3
2、3、5すべての数字を利用していますし、
また1つの文字しか使用していない式なので、
これで新しい辺の長さが求まるようになります。
内項と外項の積が等しいことから、
x(5+x)=2×3
x2+5x=6
x2+5xー6=0
(x+6)(x-1)=0
xは長さなのでx>0 x=1
IH=1
AH=5+1=6
△ABHにおいて、三平方の定理から・・
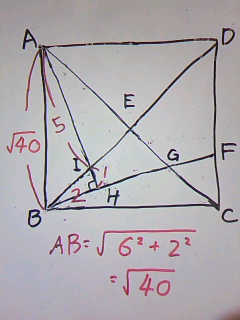
AB=√40
正方形ABCDの面積は、√40×√40=40cm2



コメント
大問2-6
点Aを通り点Bを中心とする円から、
点Aを頂点とする正三角形を描き、
点Bを通りABに垂直な直線を引く。
返信遅れて申し訳ございません。
コメント機能を見張っておくのをサボってしまいました…。
用紙から漏れそうですが、その方法は面白いですね!