平均54点
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１） 89％
10－４2
＝10－16＝－６
（２） 89％
４（２ａ＋ｂ）－２（ａ－３ｂ）
＝８ａ＋４ｂ－２ａ＋６ｂ
＝６ａ＋10ｂ
（３） 73％
ｘ2－６ｘ＋９
＝（ｘ－３）2 ←ここで代入
＝（√２＋３－３）2
＝２
（４） 57％
捕獲した27匹のうち、全体：印あり＝27：３＝９：１
47匹に印をつけたので、47×９/１＝423匹
十の位の概数なので、一の位を四捨五入→420匹
*誤答では423や430など概数処理の不適切が多かった。
（５） 62％
ア：ｘ＝４を代入すると、ｙ＝25×
イ：傾きａ＞０なので、右上がり〇
ウ：ｘ＝－２のとき、ｙ＝－３
ｘ＝１のとき、ｙ＝９
ｙの増加量は９－（－３）＝12
*一次関数の変化の割合は傾き４と同じ。
ｘの増加量が３だから、ｙの増加量は４×３＝12
エ：〇
→イ・エ
*誤答では増加量と変化の割合を誤ってウとするものが多かった。
（６） 82％
垂線の作図。捻りもなく基本問題。
Ａに針をセットして左右に交点。
２つの交点から適当な長さの弧を描き、その交点とＡを結ぶ。
大問２（関数）
（１） 82％
Ａの座標をグラフの式に放り込む。
２＝（－１）2ａ
ａ＝２
（２） 64％
Ｂのｙ座標を求める。ｙ＝２ｘ2に代入。
ｙ＝２×２2＝８
Ａ（－１、２）→Ｂ（２、８）
右に３、上に６だから、傾きは２。
Ａから右に１、上に２なので、切片は２＋２＝４
ｙ＝２ｘ＋４
*誤答では、ｙ＝２ａ＋４など間違った文字の使用が多かったらしい。
（３） 48％
底辺がＡ～Ｂのｘ座標の距離、高さがℓの切片になる。
３×４÷２＝６
大問３（確率）
（１） 67％
１個取り出し、戻したうえで再度取り出す。
１回で白玉がでる確率は２/４＝１/２
２回とも白玉は、１/２×１/２=１/４
*誤答では、玉を袋に戻さずに１/６とするものが多かった。
（２） 67％
２回とも赤玉も１/４
１/４＋１/４＝１/２
（３） 63％
２回とも違う色がでてくる確率
＝全体－２回とも同じ色＝１－１/２＝１/２
数字の組み合わせは（１、１）（１、２）（２、１）（２，２）。
２回とも数字が違う確率は２/４＝１/２
よって、２回とも色と数字が違う確率は１/２×１/２＝１/４
＠別解＠
１回目で【白１】を出したとする。２回目は【赤２】しかない。
１回目で【白２】を出したとする。２回目は【赤１】しかない。
つまり、１回目で何かを出したとき、２回目は４つのうち１つしかない。
⇒１/４
大問４（方程式）
（１）
誘導に従って穴埋め。
ＡはＱだけ作ると２割増しなので、1.2ｘ。
ア…1.2ｘ 52％
*誤答では0.2ｘが多い。
ＢはＱだけ作ると１割少なくなるので、0.9ｙ。
イ…0.9ｙ 52％
*誤答では－0.1ｙが多い。
ｘ＋ｙ＝55
1.2ｘ＋0.9ｙ＝57
この連立を解く。
ｘ＝25、ｙ＝30
ウ…25、エ…30 共に52％
オはＡでＱだけを作るとき、すなわち、1.2ｘ。
1.2×25＝30個
オ…30 47％
カはＢでＱだけを作るとき、すなわち、0.9ｙ。
0.9×30＝27個
カ…27 47％
（２） 14％！
前問より、Ｑだけの場合、１時間でＡは30個、Ｂは27個作れる。
Ａをａ台、Ｂをｂ台使うとする。
【30ａ＋27ｂ＝600】
問題文ではこれ以上手掛かりがないので、不定方程式の処理。
600は30の倍数で、30ａも30の倍数。
〔30の倍数＋30の倍数＝30の倍数〕だから、27ｂは30の倍数でなくてはならない。
30の倍数は10の倍数だから、27ｂの１の位が０となるのは270の倍数しかない。
270は30の倍数でもあり適合する。600までに270の倍数は270と540のみ。
（Ｂは複数台使うのでｂ＝０は不適）
27ｂ＝270のとき、30ａ＝600－270＝330
ａ＝11
27ｂ＝540のとき、30ａ＝600－540＝60
ａ＝２
よって、Ａの台数は２台と11台。
*誤答には20台を含めているものがあった。
@別解@
お助けマンさんから素晴らしい解法を頂きました。
30ａ＋27ｂ＝600 ←両辺を３で割る
10ａ＋９ｂ＝200
ａ＝20－９ｂ/10
ａ・ｂは自然数なので、等式が成り立つにはｂが10の倍数でなくてはならない。
ｂ＝10のとき、ａ＝11
ｂ＝20のとき、ａ＝２
よって、２台と11台。
*不定方程式はその処理に苦労する生徒が多く、正答率がガクッと下がりやすい設問です。
こちらの解法は、等式を変形させて代入すべき値を絞り込んでいます。
本問ではｂではなく、ａについて解いた方が判別が容易ですね。
なぜなのか、ｂで試してみましょう。
大問５（平面図形）
（１） 49％
△ＡＣＤ∽△ＥＢＦの証明。
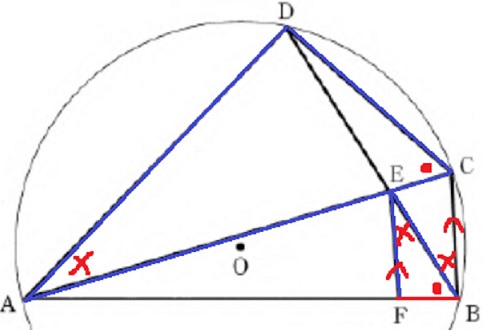
弧ＡＤに対する円周角（●）
ＥＦ//ＣＢから錯角→弧ＤＣに対する円周角（×）
２角が等しい→∽
*誤答では∠ＣＡＤ＝∠ＢＥＦを錯角を利用して適切に表現できていないものがあった。
（２）ア 43％
ＡＣが直径になる。
直径に対する円周角は直角。
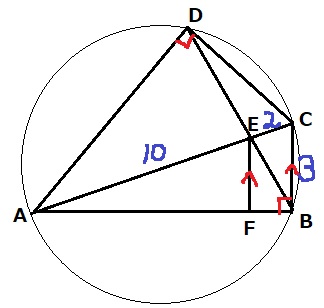
△ＡＢＣで三平方。
ＡＢ＝√（122－３2）＝３√15ｃｍ
イ 10％！
△ＡＥＦ∽△ＡＣＢ
ＡＦ：ＦＢ＝ＡＥ：ＥＣ＝10：２＝５：１
ＢＦ＝３√15×１/６＝√15/２ｃｍ
ウ 4％!!
（１）の相似を利用する。
△ＥＢＦの面積を求め、面積比は辺の比の２乗。
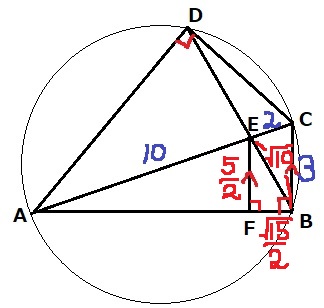
△ＡＥＦ∽△ＡＣＢから、ＥＦ＝３×10/12＝５/２ｃｍ
△ＥＢＦの面積は、√15/２×５/２×１/２＝５√15/８ｃｍ2
△ＥＢＦで三平方→ＥＢ＝√10ｃｍ
面積比は辺の比の２乗。
△ＥＢＦ：△ＡＣＤ＝√102：122＝10：144
５√15/８×144/10＝９√15ｃｍ2
大問６（規則）
（１）ア 95％
１・３・５・７…
５番目は９枚。
イ 74％
地道に数えてもできるが、
ここでどう数えるかで後ろの問題に影響する。
横と縦で分けてみよう。
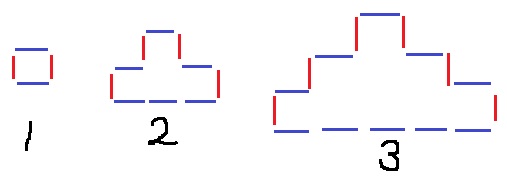
青（横）…一番下のカードの枚数×２
赤（縦）…段数×２
５番目の一番下の段は９枚だから、
９×２＋５×２＝（９＋５）×２＝28枚
（２）ア 92％
一番下のカードは、１、３、５、７…と奇数の並び。
２ｎ－１枚
イ 61％
先ほどの図の通りに考える。
一番下のカード×２＋段数（ｎ）×２
＝２（２ｎ－１）＋２ｎ
＝６ｎ－２ｃｍ
*誤答では６ｎ＋４がみられた。
（３） 70％
右のようにズラすと長方形になる。
（一番上＋一番下）×段数÷２
＝{１＋（２ｎ－１）}×ｎ÷２
＝ｎ2枚
*総和の出し方と同じ。
ex.１)～10の和は（１＋10）×10÷２＝55
（４） 8％!!
カードの境目の長さの和を求める。
今までの情報をうまく活用できないか、という思考にもっていこう。
（３）でｎ番目までのカードの総数がｎ2枚だった。
１枚の周の長さが４ｃｍなので、ｎ2枚の周りの長さは合計で４ｎ2ｃｍ。
全てのカードの周りの長さ４ｎ2ｃｍから図形の周り（外周）の長さをひけば、
カードの辺同士が重なる長さ（図形内部の線分）の和がでる。
ｎ番目の図形の周りの長さは（２）イより６ｎ－２ｃｍ。
図形内部の線分の和は、４ｎ2－（６ｎ－２）＝４ｎ2－６ｎ＋２ｃｍ。
内部の線分は隣り合うカードで１つの線分を共有するので、
ダブルで重複してカウントしている。
カードとカードの境目の長さの和は、
（４ｎ2－６ｎ＋２）÷２＝２ｎ2－３ｎ＋１ｃｍ
＠別解＠
直接求めにいくこともできる。
カードとカードの境目を横と縦で分けて考える。
横の長さをみていくと…
３番目で４ｃｍ、４番目で９ｃｍ。
４、９といえば平方数。
ｎ番目の横の長さの合計は、（ｎ－１）の平方数である。
横…（ｎ－１）2
縦の長さを観察|дﾟ)
左右で分けてみよう。
３番目…１＋２
４番目…１＋２＋３
ｎ番目…１＋２＋・・・＋（ｎ－１）
１～（ｎ－１）の総和を２倍する。
縦…（１＋ｎ－１）×（ｎ－１）÷２×２＝ｎ（ｎ－１）
したがって、（ｎ－１）2＋ｎ（ｎ－１）＝２ｎ2－３ｎ＋１ｃｍ
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
こんにちは。ご無沙汰しております。今回の岐阜県公立高校入試問題で、aについての式からの解法を紹介していただけて、とても嬉しく思います。ありがとうございました。
別件ですが、令和6年度（２０２4年度)の入試問題の解説は、まだですが、今回も昨年度のように、令和6年度の岐阜県公立高校数学入試問題の解説を賜わりますと有り難く存じます。お忙しい方ですので、お時間があれば、解答解説の掲載を宜しくお願いします。その中で大問6の（３）の問題は、悪戦苦闘の末、ようやく解答に辿り着きました。サボ先生のご解答も楽しみにしています。初めは、鋭角三角形の条件を用いて解きましたが、この鋭角三角形の条件a²<b²＋c²は高校で学習します。中学校では、発展問題扱いになっています。そこで、私は、この鋭角三角形の条件は用いずに解けましたので、サボ先生のご解答の別解が投稿できるかもしれません。これからも宜しくお願いします。お助けマンより。
コメントありがとうございます。
こちらこそご無沙汰しております。お助けマンさん、覚えてますよ！不定方程式の件ではありがとございました。
見てくださって感謝でございます。とても励みになります^^
まだ今年の岐阜はみていませんが面白そうで気になります。今は大阪Ｃと兵庫に着手しており、その次に岐阜をみますね。
至らない点など何かございましたら、またお助けを待っております。
サボ家庭教師様
こんばんは。早速のご返事、ありがとうございます。とても嬉しく思います。大阪、兵庫のあとに、岐阜の公立高校入試数学に取り組んでもらえますので、とても楽しみにしています。ありがとうございます。
サボ先生のご解答を参考に、私なりの解法を投稿出来ると有り難く存じます。これからも宜しくお願いします。岐阜のお助けマンより。
コメントありがとうございます。
いえいえ、こちらこそお越しいただきありがとうございます。
一人だと全て思いついたなと思っていても、気づかなかったことがいろいろあります。
いつでもコメントお待ちしております！解法楽しみです^^
お助けマンさんへ
2024年度の岐阜県の問題を探したのですが、ネットに見当たりませんでした。
昨年は学習塾が愛知県と一緒に出していたと思うのですが、今年は公表していないようです。
いつか出回ると思うので、そのときに問題をみて解説を書こうと思います＾＾
少々お待ちくださいませ。
サボ
おはようございます。いつもサボ先生の公立高校数学入試のご解説を拝読しているお助けマンですのです。先生のメールを今、読ませてもらいました。先生のおっしゃるように、今年度の岐阜県の公立高校数学入試問題は、サイトには掲載されていないようです。もし、宜しければ、私が読んでいるブログがございます。グーグル「ある数学愛好者のひとり言、2024岐阜県公立高校入試問題」と検索いただけますと、中日新聞掲載の問題が見られます。勿論、ブログの方も全問（大問6の（３）除く)解かれています。、私の投稿も掲載されています。この中日新聞の掲載の岐阜県の公立入試問題で宜しければ、全問解説を宜しくお願いします。お助けマンより。
こんにちは。先ほど、「ある数学愛好者のひとり言」のブログをご紹介いたしました。いかがでしょうか。このブログの中の「2024岐阜県公立高校数学入試問題」の項目を探していただき、クリックしてもらえますと、岐阜新聞の岐阜県教育委員会のコメントと入試問題とその答えが見られるかと思います。宜しくお願いします。お助けマンより。
お早うございます。
問題部分を拝見しました。
文字が薄いので少し加工する必要がありますが、図形も複雑な構図ではないのでＰＤＦ化できそうです。
お助けマンさんの解説はまだ見てません！作業前だと影響してしまうので、のちの楽しみにしております。
２～３日ほどお時間をくださいませ。
サボの家庭教師様
おはようございます。早速のご回答、ありがとうございます。私の紹介しました問題をPDF化出来ますので、とても嬉しく思います。先生の解答・解説がとても楽しみです。これからも宜しくお願いします。お助けマンより。
2024年度岐阜県の解説を書きました。
最後の問題は面白かったです＾＾
コメントはいずれに書かれても構いませんよ！こちらこそよろしくお願いします。