2024年度　三重県公立高校入試問題・前期過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－２²－７×（－５）
＝－４＋35
＝31

（２）
（２ｘ＋７）－（３ｘ－２）
＝２ｘ＋７－３ｘ＋２
＝－ｘ＋９

（３）
√75＋９/√27　（９/√27＝９/３√３）
＝５√３＋３/√３　
＝５√３＋√３
＝６√３

（４）
（ｘ－２）²－25＝－５（ｘ＋３）
ｘ²－４ｘ＋４－25＝－５ｘ－15
ｘ²＋ｘ－６
＝（ｘ＋３）（ｘ－２）＝０
ｘ＝－３、２

（５）
素数とは１と自身以外に約数をもたない、２以上の自然数。
50以上60未満の素数は53、59。

（６）
傾きが３/２なので（２、－１）から左に２、下に３移動して、
切片は－１－３＝－４
ｙ＝３/２ｘ－４

（７）
54ａｂ²÷４ｂ×２ａ
＝27ａ²ｂ　←ここで代入
＝27×２²×（－７/９）
＝－84

（８）
回転体は半径３ｃｍの半球。
底面積は半径３ｃｍの円。
【円の表面積＝４πｒ²】
３×３×π＋４π×３²÷２
＝27πｃｍ²

（９）

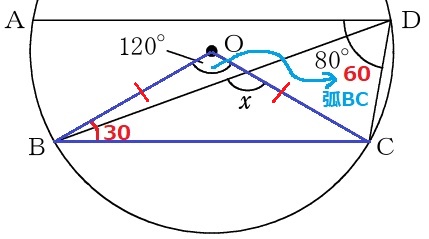
半径で△ＯＢＣは二等辺→∠ＯＢＣ＝（180－120）÷２＝30°
∠ＢＤＣは弧ＢＣの円周角だから、120÷２＝60°

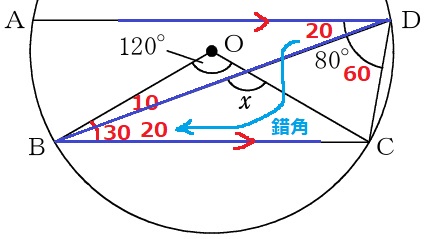
∠ＡＤＢ＝80－60＝20°
ＡＤ//ＢＣの錯角で、∠ＤＢＣ＝20°
∠ＯＢＤ＝30－20＝10°
外角定理より、ｘ＝120＋10＝130°

（10）

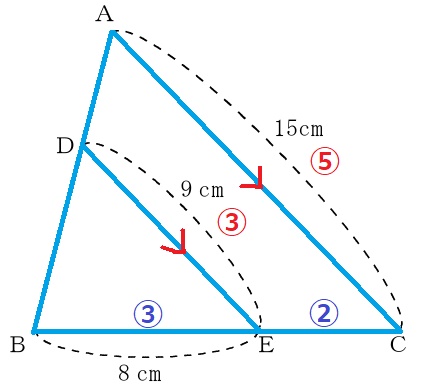
△ＡＢＣ∽△ＤＢＥより、ＡＣ：ＤＥ＝ＢＣ：ＢＥ＝⑤：③
→ＢＥ：ＥＣ＝③：②
ＥＣ＝８×②/③＝16/３ｃｍ

（11）

①∠ＯＡＰ＝90°→Ａを通るＯＸの垂線
②∠ＯＰＡ＝50°→△ＯＡＰの残りの角である∠ＰＯＡ＝180－（90＋50）＝40°
→∠ＹＯＸ＝80°の二等分線をひけばいい。
③交点にＰを記す。

大問２（データの活用）

（１）

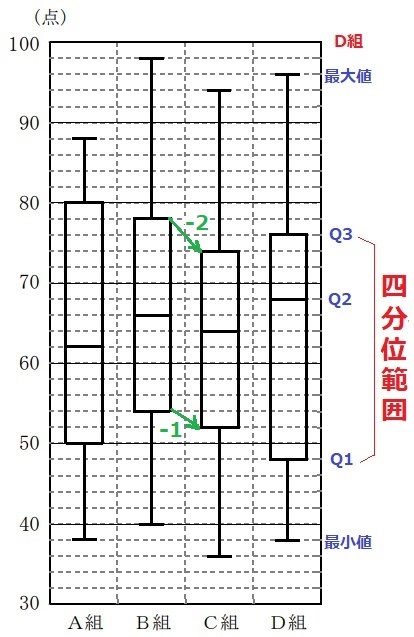
中央値（Q2）が最も大きいのはＤ組。
１目盛りは２点。
68点

（２）
四分位範囲＝第３四分位数（Ｑ3）－第１四分位数（Q1）
箱の長さが最も短い組を調べる。
Ｂ組→Ｃ組の変化をみると、Ｑ3は－２目盛り、Ｑ1は－１目盛り。
最も小さいのはＣ組。
その第１四分位数は52点。

（３）
80点以上が最も多いのは、Ｑ３が80点であるＡ組。
31人の中央値は16番目。Ｑ３は上位15人の真ん中、上から８番目の値。
80点以上の人数がＡ組は少なくとも８人以上いるが、他の組は８人未満。
ア

大問３（確率）

（１）
全体は６枚から２枚ひく組み合わせ→_６Ｃ_２＝15通り
２枚の積が正の数となる→正２枚か負２枚をひく。
●正２枚
〔１～３〕から２枚ひく→選ばない１枚を選ぶ→３通り
●負２枚
〔－３～－１〕から２枚ひく→同様に３通り
計６通り。
確率は６/15＝２/５

（２）
正と負の組み合わせだと、積は大きく負に傾く。
和＜積の方が少ないので、余事象から攻める。
まず、負同士をひいて積を大きく正に傾かせる。
⇒（－３、－２）（－３、－１）（－２、－１）の３通り。
正同士の場合、１を含むと和の方が多くなるので和＜積は（２、３）のみ。
計４通り。
和＞積は15－４＝11通りだから、確率は11/15。

大問４（平面図形）

（１）
△ＡＢＧ≡△ＣＥＩの証明。

正方形の辺と内角→ＡＢ＝ＣＥ、∠ＢＡＧ＝∠ＥＣＩ
両端角が使えそう。直角を利用する。

∠ＡＢＣ＝90°→∠ＡＢＧ＝90－∠ＨＢＥ（●）
∠ＢＨＥ＝90°→△ＢＨＥの残りの角より、
∠ＣＥＩ＝180－（90＋∠ＨＢＥ）＝90－∠ＨＢＥ（●）
∠ＡＢＧ＝∠ＣＥＩ
１辺と両端角が等しいので合同。

（２）

ＩＣを対称の軸とすると、△ＣＥＩと△ＣＢＩは線対称で合同。

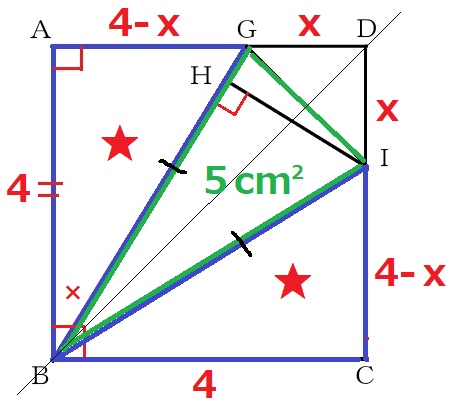
★は合同、ＧＡ＝ＩＣ→ＤＧ＝ＤＩ
（ＢＤを対称の軸とすると線対称）
求めたいＤＩをｘとすると、ＩＣは４－ｘ。

面積の合計から等式を立てる。
△ＢＣＩ（★）×２＋△ＤＩＧ＝正方形－５
４（４－ｘ）÷２×２＋ｘ²/２＝11
ｘ²/２－４ｘ＋５＝０　←×２
ｘ²－８ｘ＋10＝０
解の公式を適用、ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝４±√６
０＜ｘ＜４より、ｘ＝４－√６
４－√６ｃｍ

大問５（関数）

（１）①
ｙ＝－10/ｘにおいて、
ｘ＝２のとき、ｙ＝－５
ｘ＝５のとき、ｙ＝－２
変化の割合＝ｙの増加量÷ｘの増加量
＝｛－２－（－５）｝÷（５－２）
＝３÷３＝１

②

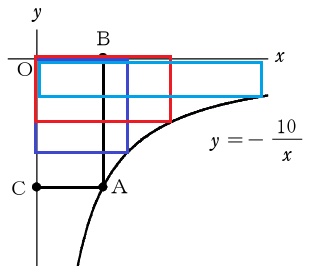
反比例はｘとｙの積が比例定数で一定。
長方形の横ｘと縦ｙの積である長方形の面積は一定。
（比例定数は－10、絶対値の10で一定）
ウ

（２）①
ｙ＝ａｘ²に（４、４）を代入。
４＝16ａ
ａ＝１/４

②

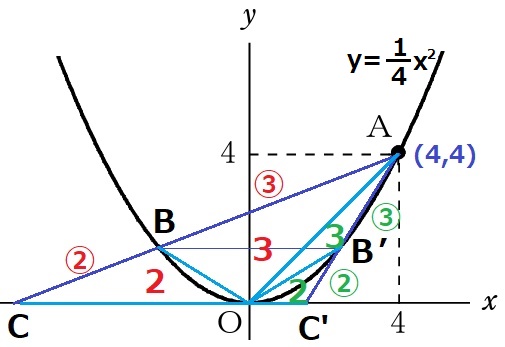
Ｂはグラフ上の点で、ＡＢを延長したｘ軸との交点がＣ。
延長するとｘ軸に交わるので、ＢはＡより下にある
△ＯＢＣ：△ＯＡＢ＝ＣＢ：ＢＡ＝２：３
Ｂのｘ座標が正か負で２通りある。

ＢとＢ’のｙ座標は同じ。ｙ＝４×②/⑤＝８/５
これをｙ＝１/４ｘ²に代入する。
８/５＝１/４ｘ²
ｘ²＝32/５
ｘ＝±４√２/√５＝±４√10/５

大問６（方程式）

（１）①
あんまん100円、肉まん140円。
420＝140×３しかない。
肉まん３個→エ

②
肉まん３個を10人が買った。
肉まん30個→エ

（２）①

260はあんまん、250は肉まんの個数の合計。
つまり、それぞれの合計個数で等式を立てている。
最初の文字は何を示しているのか。340円と380円の内訳を調べると、
340円＝あんまん２個＋肉まん１個、380円＝あんまん１個＋肉まん２個
・・ということは、Ｃ・Ｄには残りのあんまんと肉まんの個数の合計が入る(;´･ω･)

１個ずつ内訳を調べ、支払った人数をかけて合計を出す。
あんまん：40＋40＋50＋30＝160個
肉まん：33＋50＋30＋30＝143個
Ｃ…160、Ｄ…143

②
前問の連立を解く。
２ｘ＋ｙ＋160＝260
２ｘ＋ｙ＝100　…①
ｘ＋２ｙ＋143＝250
ｘ＋２ｙ＝107　…②

①×２－②をすると、３ｘ＝93
ｘ＝31
①に代入。２×31＋ｙ＝100
ｙ＝38
Ⅰ…31、Ⅱ…38