2023年度　鳥取県公立高校入試問題過去問【数学】解説

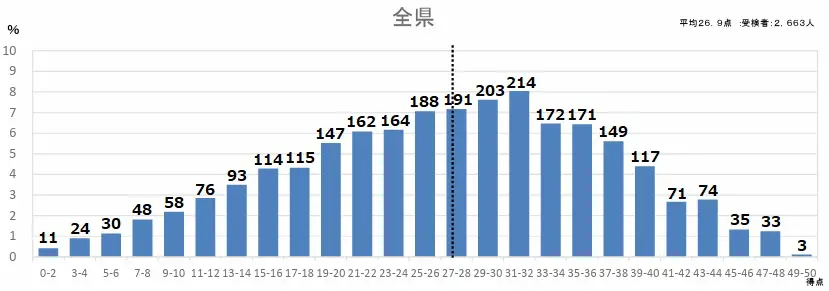
平均26.9点（前年比；＋0.2点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　96.8％
－６－（－２）
＝－６＋２
＝－４

②　96.8％
－２/３÷８/９
＝－３/４

③　87.1％
６√２－√18＋√８
＝６√２－３√２＋２√２
＝５√２

④　89.0％
４（２ｘ＋１）－３（２ｘ＋１）
＝８ｘ＋４－６ｘ－３
＝２ｘ＋１

⑤　83.2％
３ｘｙ×２ｘ³ｙ²÷（－ｘ³ｙ）
＝－６ｘｙ²

（２）　92.9％
ｘ²－３ｘ＋２
＝（ｘ－１）（ｘ－２）

（３）　78.1％
３ｘ²－ｘ－１＝０
解の公式を適用して、ｘ＝（１±√13）/６

（４）　72.3％
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
２（１＋４）＝10

（５）　81.3％

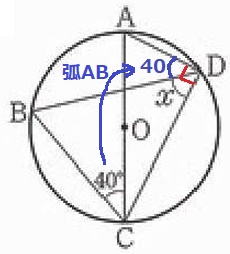
半円の弧に対する円周角→∠ＡＤＣ＝90°
弧ＡＢの円周角→∠ＡＤＢ＝40°
ｘ＝90－40＝50°

（６）　60.6％
全体は４×４＝16通り
ａ＋ｂが24の約数となる組み合わせを調べる。
●１→なし
●２→（１、１）
●３→（１、２）（２、１）
●４→（１、３）（３、１）（２、２）
●６→（２、４）（３、３）（４、２）
●８→（４、４）
最大数は８なので、もうない。
計10通り、確率は10/16＝５/８

（７）　32.3％！
面積が168ｎｍ²の１辺の長さ＝√（168ｎ）＝２√（42ｎ）ｍ
根号を外すには、42×（平方数）をかければいい。
最小値ｎ＝42×１²＝42

（８）①　58.1％
連続する２つの偶数の積が８の倍数であることを証明する。
小さい方を２ｎとすると、大きい方は２ｎ＋２。
２ｎ（２ｎ＋２）＝４ｎ（ｎ＋１）

ｎ（ｎ＋１）は連続する２つの整数だから、この部分は２の倍数。
ｍを整数として、ｎ（ｎ＋１）を２ｍに置き換えると、
４ｎ（ｎ＋１）＝４×２ｍ＝８ｍ
ｍは整数だから、２ｎ（２ｎ＋２）は８の倍数である。
したがって、連続する２つの偶数の積は８の倍数である。
ア…２ｎ＋２、イ…４

②　28.4％！
連続する２つの整数の積が２の倍数になる理由。
ｎ、ｎ＋１はどちらか一方が偶数だから、ｎ（ｎ＋１）は２の倍数である。

（９）　35.5％

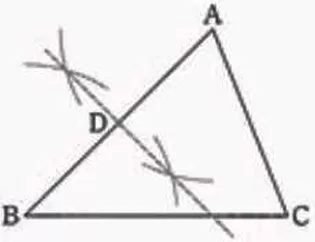
Ｃを通る△ＡＢＣを二等分する線分→ＤはＡＢの中点
ＡＢの垂直二等分線とＡＢとの交点がＤ。

（10）①　71.6％
ＯＰ＝ＯＱの証明。

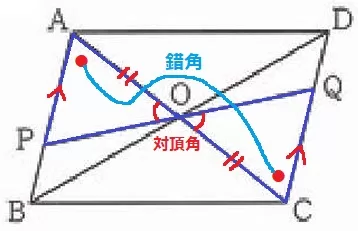
△ＯＡＰと△ＯＣＱにおいて、
対頂角より、∠ＡＯＰ＝∠ＣＯＱ
ＡＢ//ＤＣの錯角より、∠ＯＡＰ＝∠ＯＣＱ
ａ…イ、ｂ…エ

②　73.5％
（続き）
平行四辺形の対角線は、それぞれの中点で交わるから、
ＯＡ＝ＯＣ
ｃ…ウ、ｄ…カ

（３）　72.3％
（続き）
以上より、１辺と両端角が等しいから合同。

大問２（データの活用）

（１）　80.6％

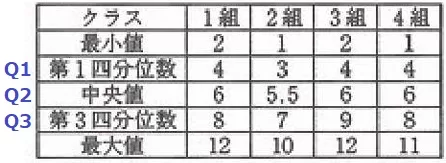
四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
最も大きいのは３組。９－４＝５冊
クラス…３組、四分位範囲…５冊

（２）　94.2％

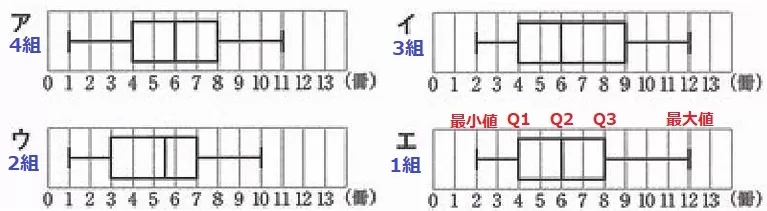
最小値・最大値だけでイ・エと絞られる。
Q3の違いからエ。

（３）①　73.5％

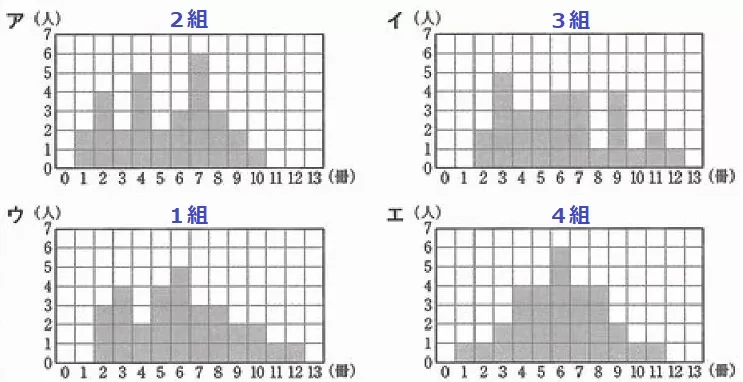
ここも最小値・最大値からイ・ウ。
30人のQ3は上位15人の真ん中、上から８番目の値。
８番目が８冊なのはウ。
（＊他の組は上図のようになる）

②　69.7％
30人×0.2＝30×１/５＝６人
７冊が６人なのはアの２組。

③　60.6％

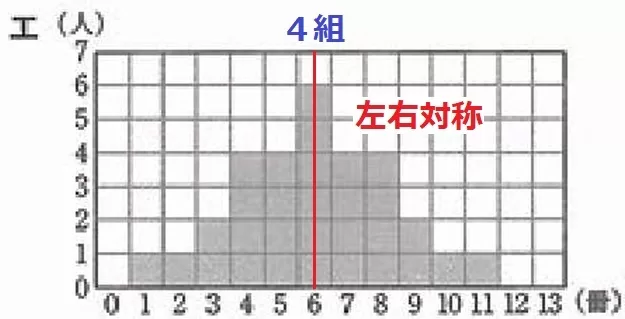
４組のヒストグラムはエ。
よく見ると、ヒストグラムの形が左右対称である。
５と７、４と８、３と９…とペアで均すと６になる。
平均値は６冊。

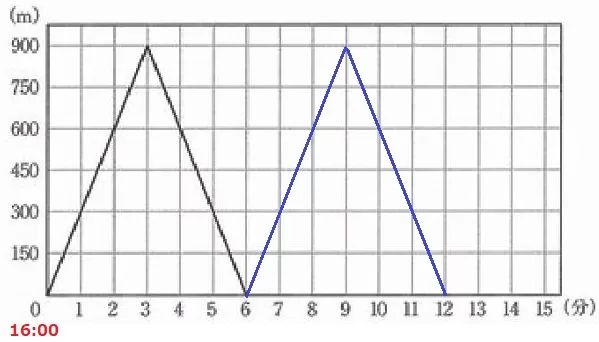
大問３（数量変化）

（１）　77.4％

２往復するから16時12分。

（２）①　54.2％
学校～時計店がａ分、時計店～公園がｂ分。
１つ目は時間で等式。
16時２分に出発して、16時15分に到着した。
ａ＋ｂ＋２＝15　…①
２つ目は学校～公園までの距離で等式。
50ａ＋75ｂ＝900　…②

②　45.8％
前の連立を解く。
ａ＋ｂ＝13　←50倍
50ａ＋50ｂ＝650　…③
50ａ＋75ｂ＝900　…②
②－③をすると、25ｂ＝250
ｂ＝10
ａ＝13－10＝３
学校～時計店の距離は、分速50ｍ×３分＝150ｍ

③　60.0％

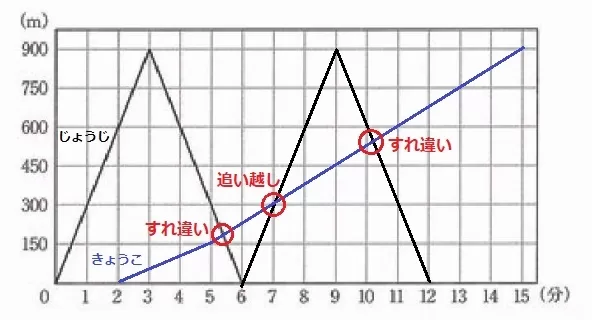
きょうこのグラフを追加。
出発から３分後に150ｍ地点の時計店に着く。
（２、０）→（５、150）→（15、900）を通過する。
交点を数えると３回。

④　6.5％!!

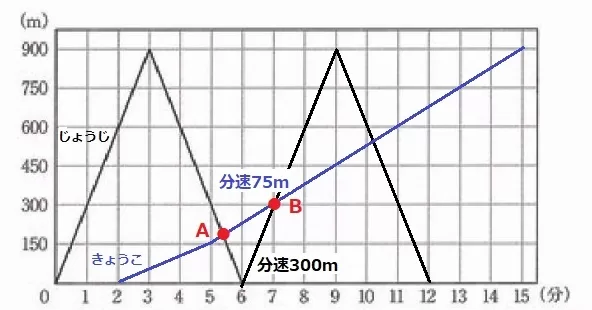
ＡＢ間の時間を求める。
Ｂはちょうど格子点で、（７、300）の点である。

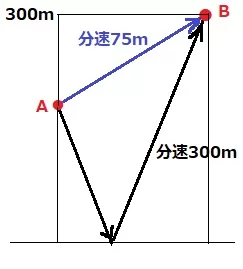
ＡＢ間において、じょうじときょうこの移動距離の合計は600ｍである。
２人は１分間で375ｍ移動するから、600÷375＝８/５分

大問４（空間図形）

（１）　77.4％

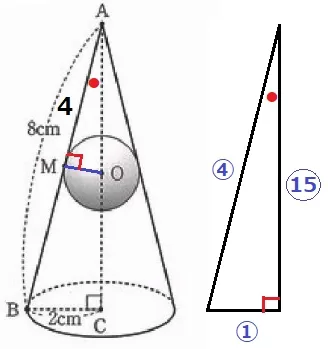
△ＡＢＣにおいて、ＡＢ：ＢＣ＝８：２＝④：①
辺の比で三平方をすると、ＡＣ＝〇√15
高さＡＣ＝２×〇√15＝２√15ｃｍ

（２）　5.2％!!
球の半径ＯＭはＡＢとＭで接する→ＯＭ⊥ＡＢ
２角相等から、△ＡＢＣ∽△ＡＯＭ
ＡＭ：ＯＭ＝〇√15：①だから、ＯＭ＝４×①/〇√15＝４√15/15ｃｍ

（３）①　12.3％！

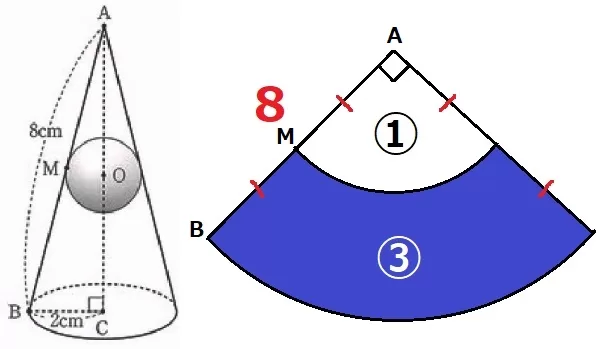
円錐の側面積は扇形。中心角の処理は〔×半径/母線〕で対処する。
立体Ｑの側面積は青いエリア。
小さい扇形：大きい扇形の相似比は１：２→面積比は①：④だから青は③にあたる。
８×８×π×２/８×③/④＝12πｃｍ²

②　6.5％!!

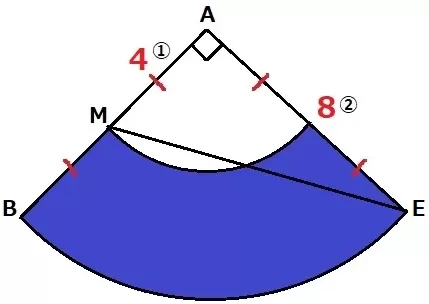
扇形の中心角は、360×半径/母線＝360×２/８＝90°⇒三平方が使える。
ＡＭ：ＡＥ＝４：８＝①：②　
△ＡＭＥで三平方→ＭＥの辺の比は〇√５
ＭＥ＝４×〇√５＝４√５ｃｍ

大問５（数量変化２）

（１）①　60.6％、61.9％

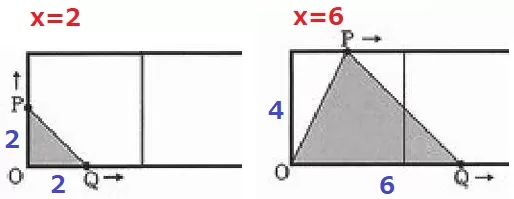
０≦ｘ≦４は直角二等辺。
４≦ｘ≦12は高さが４一定で、底辺だけが長くなる。
ｘ＝２のとき、ｙ＝２×２÷２＝２
ｘ＝６のとき、ｙ＝６×４÷２＝12

②　41.3％

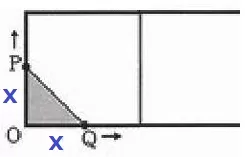
０≦ｘ≦４のときは、１辺がｘの直角二等辺。
ｙ＝１/２ｘ²

③　48.4％
０≦ｘ≦４は底辺と高さがともに伸びるので、ｙ＝ａｘ²で増加する。

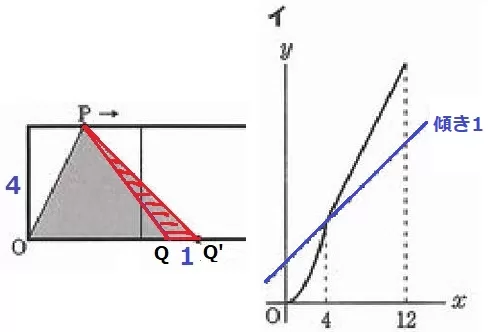
上図は４≦ｘ≦12のとき、Ｑが１秒後にＱ’に移動したとする。
増加した面積は、１×４÷２＝２
ｘが１増えるとｙは２増える→変化の割合は２→傾きは２。
傾きが１より大きいイ。

（２）ア…31.6％！、イ…23.2％！、ウ…12.9％！

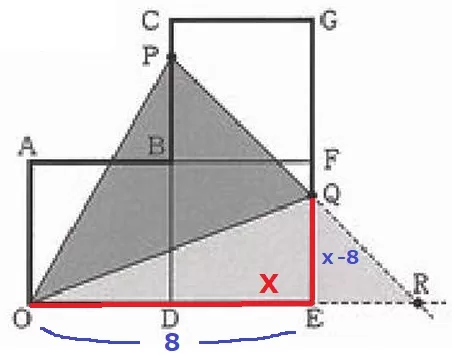
まず、ＥＱ＝ｘ－８の理由を確認しておく。
Ｑの移動距離：ＯＥ＋ＥＱ＝ｘ
ＥＱ＝（ＯＥ＋ＥＱ）－ＯＥ＝ｘ－８

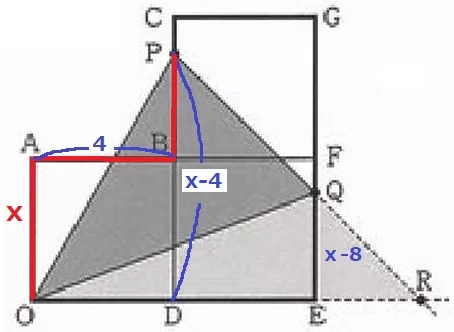
Ｐの移動距離：ＯＡ＋ＡＢ＋ＢＰ＝ｘ
ＤＰ＝ＯＡ＋ＢＰ＝（ＯＡ＋ＡＢ＋ＢＰ）－ＡＢ＝ｘ－４

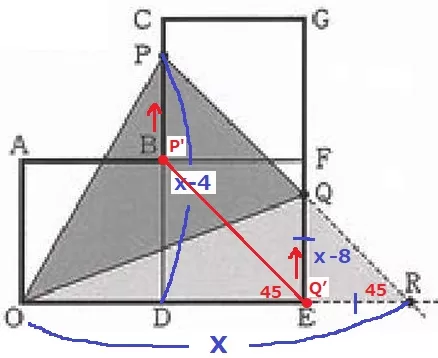
なんとなくＥＱ＝ＥＲに見える。
ＢＥに補助線。
８秒後にＰはＢ、ＱはＥにいる。
そこからＰとＱは同じ速さで上に向かうので、ＢＥとＰＱは平行である。
ＢＥは正方形ＢＤＥＦの対角線だから、∠ＢＥＤ＝45°
同位角で∠ＰＲＤ＝45°
△ＱＥＲは内角が45°―45°―90°→直角二等辺ゆえ、ＥＱ＝ＥＲ
ＯＲ＝ＯＥ＋ＥＲ＝ＯＥ＋ＥＱ＝ｘ

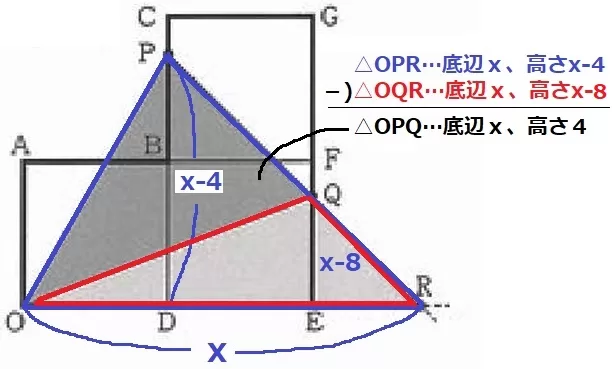
△ＯＰＱ＝△ＯＰＲ－△ＯＱＲ
底辺ｘ、高さ（ｘ－４）の△ＯＰＲから、
底辺ｘ、高さ（ｘ－８）の△ＯＱＲをひくと、
底辺ｘ、高さの差４ｃｍの三角形が△ＯＰＱと等積である。
ｙ＝ｘ×４÷２＝２ｘ
ア…ｘ－４、イ…ｘ、ウ…２ｘ

（３）　6.5％!!

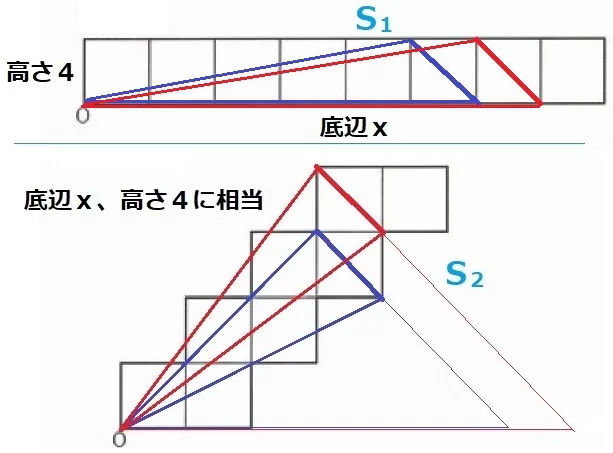
↑青線はｘ＝24、赤線はｘ＝28を示す。
正方形を階段状につなげた場合、前問よりＳ₂は底辺ｘ、高さ４ｃｍの三角形に相当するので、
結局、Ｓ₂とＳ₁は面積が等しい。
Ｓ₁：Ｓ₂＝１：１