2022年度　大阪府公立高校入試Ｂ問題過去問【数学】解説

平均57.5点（前年比；－2.7点）
問題はコチラ→ＰＤＦファイル
2022年度・大阪（数学）Ａ問題、Ｃ問題の解説はコチラ。

大問１（計算）

（１）　89.4％
18－（－４）²÷８
＝18－16÷８
＝18－２
＝16

（２）　93.1％
２（５ａ－ｂ）－３（ａ＋６ｂ）
＝10ａ－２ｂ－３ａ－18ｂ
＝７ａ－20ｂ

（３）　79.7％
14ａｂ÷７ａ²×ａｂ
＝２ｂ²

（４）　75.8％
（ｘ＋１）（ｘ－１）－（ｘ＋３）（ｘ－８）
＝ｘ²－１－（ｘ²－５ｘ－24）
＝ｘ²－１－ｘ²＋５ｘ＋24
＝５ｘ＋23

（５）　56.3％
（√６－√２）²＋√27
＝６－２√12＋２＋３√３
＝８－４√３＋３√３
＝８－√３

大問２（小問集合）

（１）　66.0％
ｂ＝（５ａ＋４）/７　…両辺×７
７ｂ＝５ａ＋４　…移項
５ａ＝７ｂ－４　…両辺÷５
ａ＝（７ｂ－４）/５

（２）　70.0％
２ｘ²－３ｘ－１＝０
解の公式を適用して、
ｘ＝（３±√17）/４

（３）　54.6％
平均値ａ…（２×１＋３×４＋４×３＋５×２＋６×１＋12×１）÷12＝54÷12＝4.5冊
最頻値ｂ…最もあらわれている値で３冊。
中央値ｃ…12人のメジアンは６番目と７番目の平均で４冊。
ｂ＜ｃ＜ａ
エ

（４）　59.0％
２枚の取り出し方→３×４＝12通り
20の約数は【１・２・４・５・10・20】
◆１→ない
◆２→（１、１）
◆４→（１、３）（３、１）
◆５→（２、３）
◆10→（３、７）
◆20→ない
計５通りで、確率は５/12。

（５）　69.7％
最も小さい整数をｎとすると、連続する３つの整数はｎ、ｎ＋１、ｎ＋２。
ｎ＋（ｎ＋１）＋（ｎ＋２）
＝３ｎ＋３＝2022
ｎ＝673

（６）　24.5％！

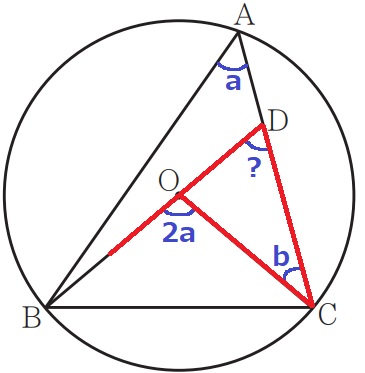
孤ＢＣに対する中心角より、∠ＢＯＣ＝２ａ
△ＯＣＤで外角定理→∠ＣＤＯ＝２ａ－ｂ°

（７）　54.8％
４＜√ｎ＜５　←すべて２乗して根号を外す
16＜ｎ＜25　…①

√（６ｎ）が自然数→６ｎが平方数で根号が外れる。
ｎは〔６×平方数〕である。
ｎ＝１→６×１²＝６
ｎ＝２→６×２²＝24
①の範囲にあるのはｎ＝24

（８）　23.8％！
答案では途中式を含めた求め方も書く。
手順どおりに機械的に処理していく。

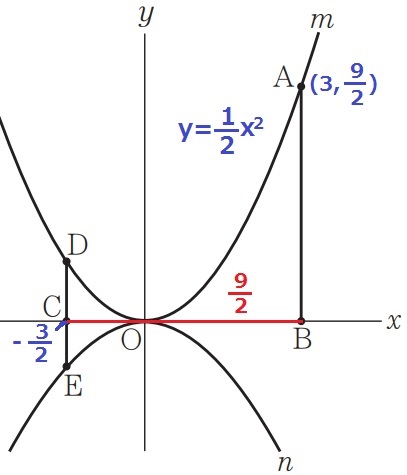
ｙ＝１/２ｘ²にｘ＝３を代入、Ａ（３、９/２）
ＣＢ＝９/２だから、Ｃのｘ座標は３－９/２＝－３/２

ｙ＝１/２ｘ²にｘ＝－３/２を代入、Ｄ（－３/２、９/８）
ｙ＝ａｘ²にｘ＝－３/２を放り込んで、Ｅ（－３/２、９/４ａ）
ＤＥ＝２だから、９/８－９/４ａ＝２　←８倍
９－18ａ＝16
ａ＝－７/18
（*ａ＜０の条件に適合する）

大問３（関数）

（１）①ア…93.8％、イ…86.9％
15が足される回数はあいだの数、つまり、（ｘ－１）回である。
ｘ＝４のとき、ｙ＝320＋15×（４－１）＝365
ｘ＝８のとき、ｙ＝320＋15×（８－１）＝425
ア…365、イ…425

②　78.8％
規則を一般化する。
ｙ＝320＋15（ｘ－１）
ｙ＝15ｘ＋305

③　80.4％
先ほどの式にｙ＝620を代入する。
620＝15ｘ＋305
ｘ＝21

（２）　43.3％
コーンＡ；ｙ＝15ｓ＋305
コーンＢ；ｙ＝150＋10（ｔ－１）＝10ｔ＋140

コーンＡとコーンＢの合計が39個だから、ｓ＋ｔ＝39　…①
高さが同じ⇒ｙの値が等しいので、15ｓ＋305＝10ｔ＋140　…②

①、②の連立を解けばよいが、処理が面倒くさい(´д`)
②を整理すると、10ｔ－15ｓ＝165　…③
①×10－③でｓ＝９
①に代入してｔ＝30
ｓの値…９、ｔの値…30

＠別解＠
こういう面倒な方程式をみると、どうにか回避できないものかという衝動に駆られる…。
増加分はコーンの個数のあいだの数なので、あらかじめＡとＢを１個ずつ置いておく。
残りは合計37個。
ＡとＢの差は、320－150＝170ｃｍ
高さを同じくするため、170÷10＝17個のＢを積む。

積み上げる高さが等しくなるように、残り20個を配分する。
増加する長さの比はＡ：Ｂ＝15：10＝３：２
積むべきコーンの個数は逆比でＡ：Ｂ＝②：③
Ａは20×②/⑤＝８個積む。
最初の１個と合わせて、Ａは９個。
Ｂの個数は、39－９＝30個

大問４（図形）

（１）　48.6％
△ＢＣＥ∽△ＤＦＨの証明。

仮定より、∠ＣＥＢ＝∠ＦＨＤ＝90°
平行四辺形ＡＢＣＤの対角と対頂角より、∠ＥＢＣ＝∠ＨＤＦ
２角相等で∽。

（２）①　56.0％
前問の相似を利用する。
ＦＤ：ＤＨ＝ＣＢ：ＢＥ
５：２＝６：ＢＥ
ＢＥ＝２×６/５＝12/５ｃｍ

②　6.0％!!
 
△ＦＧＤの底辺をＧＤとすると高さはＦＨ。
△ＦＤＨで三平方→√21ｃｍ

ＧＤの長さを知りたい。
△ＦＧＤと相似にあたるのは△ＥＧＡ。

先ほどのＢＥを手がかりに、ＡＥ＝７－12/５＝23/５ｃｍ
△ＥＧＡ∽△ＦＧＤより、相似比はＡＥ：ＤＦ＝23/５：５＝㉓：㉕＝ＡＧ：ＧＤ
ＧＤ＝６×㉕/㊽＝25/８ｃｍ
よって、△ＦＧＤの面積は、25/８×√21÷２＝25√21/16ｃｍ²

（３）　77.5％

ネジレ⇒平行ではない、かつ延長しても交わらない。
辺ＡＤとネジレにあるのは辺ＥＦと辺ＦＢ。
ウ・エ

（４）①　13.6％！

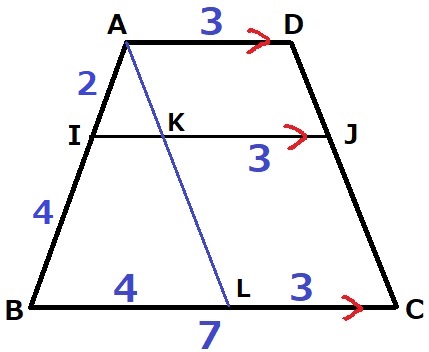
ＡＤ//ＩＪ//ＢＣ。
Ａを通るＤＣに平行な線をひき、ＩＪ、ＢＣとの交点とＫ、Ｌとする。
平行四辺形は対辺が等しいから、ＡＤ＝ＫＪ＝ＬＣ＝３ｃｍ
ＢＪ＝７－３＝４ｃｍ
△ＡＩＫ∽△ＡＢＬより、ＩＫ＝４×２/６＝４/３ｃｍ
ＩＪ＝４/３＋３＝13/３ｃｍ

②　2.3％!!

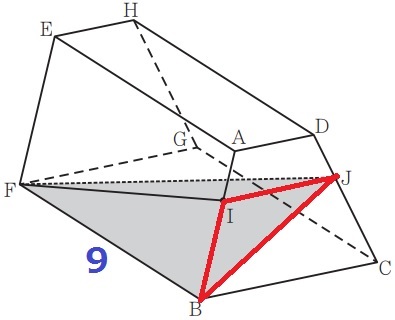
立体は四角柱⇒面ＡＢＣＤ⊥面ＦＢＣＧ。
面ＡＢＣＤ上にある△ＩＢＪを底面とすると、高さはＦＢ＝９ｃｍ
△ＩＢＪの面積さえわかればいい。

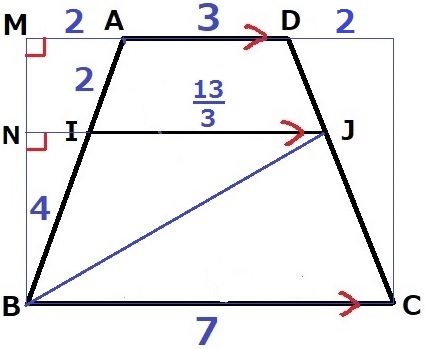
△ＩＢＪの高さが知りたい。
ＡＢ＝ＤＣ＝６ｃｍの台形ＡＢＣＤは左右対称な等脚台形である。
ＡＤ、ＩＪの延長線にＢから垂線をひき、交点をＭ、Ｎとする。
ＭＡ＝（７－３）÷２＝２ｃｍ
△ＭＡＢで三平方→ＭＢ＝４√２ｃｍ
△ＭＡＢ∽△ＮＩＢより、ＮＢ＝４√２×４/６＝８√２/３ｃｍ
求積すべき立体の体積は、13/３×８√２/３÷２×９÷３＝52√２/３ｃｍ³
公立高校入試解説ページに戻る