2020年度　岡山朝日高校過去問【数学】解説

45分試験
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

①
しょっぱなの計算にやられる(;`ω´)

指数処理で符号を取り違えないように！最後は８で通分。
５√２

②
シンプルだが変化球でビビる。。

中心角を□とおいてしまおう。
□＝１/π
角度で示すと360°×１/πでやりにくい(´･_･`)
弧の長さは２ｃｍ。

③
ｙ＝ｘ²において－２≦ｘ≦１のとき、
ｘ＝０のとき　最小値ｙ＝０
ｘ＝－２のとき　最大値ｙ＝４
ｙの変域は０≦ｙ≦４

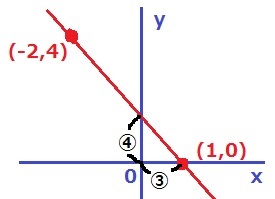
ａ＜０なので、ｙ＝ａｘ＋ｂは右下。
－２≦ｘ≦１のとき、０≦ｙ≦４だから、
ｘ＝－２のとき　最大値ｙ＝４
ｘ＝１のとき　最小値ｙ＝０
（－２、４）（１、０）の点を通過する。
右に３、下に４だから、傾きは－４/３。
切片は、１×④/③＝４/３
（１）…－４/３（２）…４/３

④
ａが平方数であれば根号が外れて整数となる。
ａ＝25、36、64
３通り

５枚から連続して２回とるので、５×４＝20通り
確率は３/20。

⑤
８人の合計…12×８＝96点
ａ²＋ａ＝96－（13＋18＋20＋19＋４＋10）
＝96－84＝12
ａ²＋ａ－12
＝（ａ＋４）（ａ－３）＝０
ａ＞０より、ａ＝３
ａ²＝９

８人の中央値は４番目と５番目の平均値。
10と13の平均→11.5点
（１）９（２）11.5点

⑥
作図。条件に合う点Ｐをつくるには、どのような方法をとればいいか。

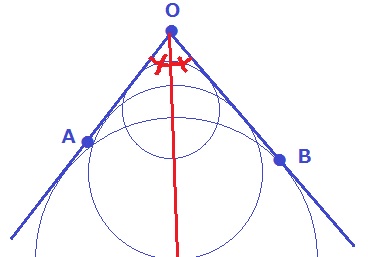
（条件１）半直線ＯＡとＯＢに接する円
→円の中心Ｐは∠ＡＯＢの二等分線上にある。

（条件２）∠ＰＡＢ＝∠ＰＢＡ
→ＡＢの垂直二等分線を対称の軸とすると、対応する角の大きさが等しい。
（１）イ（２）オ

大問２（方程式）

（解答では途中式も記述する）
徒歩の人数…360×５％＝18人
求めたいバスをｘ人とすると、自転車は３ｘ＋９人。
電車は（３ｘ＋９）÷５＝0.6ｘ＋1.8人

18＋ｘ＋（３ｘ＋９）＋（0.6ｘ＋1.8）＝360
4.6ｘ＝331.2
ｘ＝72
72人

大問３（空間図形）

①
途中式も記述する。
台形の下底ＢＣが知りたいところ。

ＡからＢＣに垂線、足をＨとする。
△ＡＢＨで三平方→ＢＨ＝１ｃｍ
ＢＣ＝１＋５＝６ｃｍ
台形ＡＢＣＤの面積は、（５＋６）×２÷２＝11ｃｍ²

②
四角柱Ｓの高さは88ｃｍ³÷11ｃｍ²＝８ｃｍ

ＡＢ//ＰＱより、同位角で∠ＡＢＨ＝∠ＰＱＣ
△ＡＢＨと△ＰＱＣは２角が等しく相似！

△ＰＱＣは直角三角形で、最も長い辺は斜辺のＰＱ。
三角柱Ｔの側面で面積が最大となる長方形はＰＱを１辺とする。
三角柱Ｔの高さは四角柱Ｓと同じ８ｃｍだから、ＰＱ＝４√10÷８＝√10/２ｃｍ

△ＡＢＨの面積…１×２÷２＝１ｃｍ²
三角ＡＢＨと△ＰＱＣの面積比を求める。
ＡＢ：ＰＱ＝√５：√10/２＝２√５：√10＝２：√２
面積比は辺の比の２乗なので、△ＡＢＨ：△ＰＱＣ＝２²：（√２）²＝２：１
△ＰＱＣの面積…１×１/２＝１/２ｃｍ²

三角柱Ｔの体積…１/２×８＝４ｃｍ³

大問４（平面図形）

①

三平方ですばやく出そう！
（１）２√３（２）２（３）４

②
△ＡＥＦ∽△ＥＣＦの証明。
３辺の比がわかっているので、それに着目する。
ＡＥ：ＥＦ：ＦＡ＝ＥＣ：ＣＦ：ＦＥ＝√３：２：１
３辺の比が等しいから∽。

③
円の中心であるＧ・Ｈの位置を特定する。

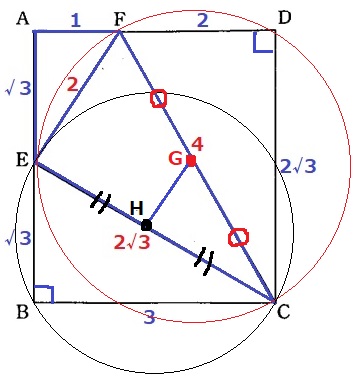
直径に対する円周角は90°！
∠ＣＤＦ＝90°から、円Ｏの中心Ｇは直径ＣＦの中点にある。
∠ＥＢＣ＝90°から、円Ｏ’の中心Ｈは直径ＣＥの中点にある。

さらに、△ＣＧＨと△ＣＦＥにおいて、ＧとＨは各々の辺の中点だから、
中点連結定理により、ＧＨ＝２÷２＝１ｃｍ

④
きっつい:;(∩´＿`∩);:

↑このエリアを求めなさいっちゅーことだが戦意喪失するね！
しかし、この問題だけ解説を書かない訳にはいかないので頑張りました。

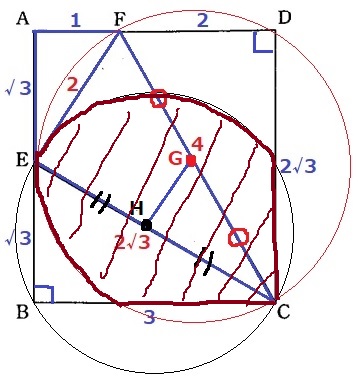
長さがよくわかっていないので角度の調査。
こういうヘンテコな図形には有名角が隠れているのが定石です|дﾟ)
ＥＣより下と上で分割し、さきに下の部分を求めにいきます。

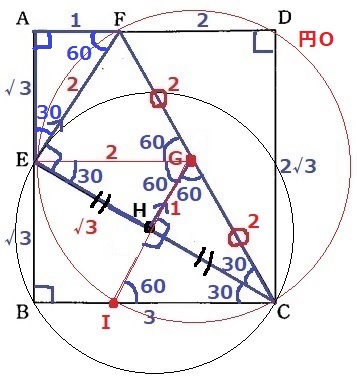
△ＡＥＦは１：２：√３の直角三角形→内角は30°－60°－90°
（２）の△ＡＥＦ∽△ＥＣＦより、△ＥＣＦの内角も30°－60°－90°。
∠ＣＥＦ＝90°だから、Ｅも円Ｏの円周上にある。

ＥＧに補助線。
円Ｏの中心Ｇに注目。
ＦＧ＝４÷２＝２、半径からＥＧ＝２、ＥＦ＝２。
△ＥＦＧは３辺が等しい正三角形。
また、△ＥＧＨは辺の比が１：２：√３→内角が30°－60°－90°の直角三角形！
△ＣＧＨも内角もこれと等しく、ＥＨ＝ＨＣから一辺と両端角相等で△ＥＧＨ≡△ＣＧＨ。

円Ｏと辺ＢＣ上（Ｃ以外）の交点をＩとする。ＧＩに補助線。
∠ＡＥＦ＝30°→∠ＢＥＣ＝60°→△ＢＥＣの残りの内角で∠ＥＣＢ＝30°→∠ＧＣＩ＝60°
半径からＧＩ＝ＧＣ→△ＧＣＩの内角がすべて60°となり正三角形。
（*∠ＩＨＣ＝ＧＨＣ＝90°となり、Ｇ―Ｈ―Ｉは一直線）

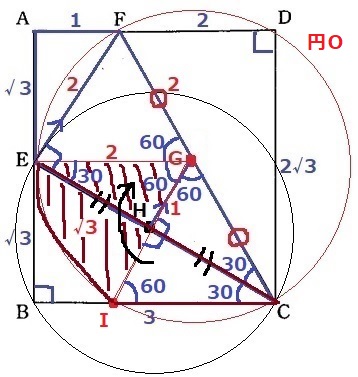
△ＥＧＨと△ＣＩＨは一辺と両端角が等しく合同。
△ＣＩＨを△ＥＧＨに移植すると、半径２ｃｍ中心角60°の扇形になる。
２×２×π×60/360＝２/３πｃｍ²

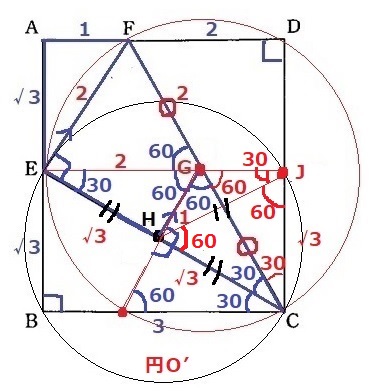
 つづいて上の部分にいきます(;´Д｀)ｲﾔ-
円Ｏ’と辺ＣＤ（Ｃ・Ｄ以外）の交点をＪとする。
∠ＧＣＪ＝90－60＝30°
半径から△ＨＪＣは二等辺で、底角の∠ＨＣＪ＝60°だから、
△ＨＪＣの内角はすべて60°で正三角形！
（*ＪＣ＝√３となり、四角形ＥＢＣＪは長方形→Ｅ―Ｇ―Ｊは一直線といえる）

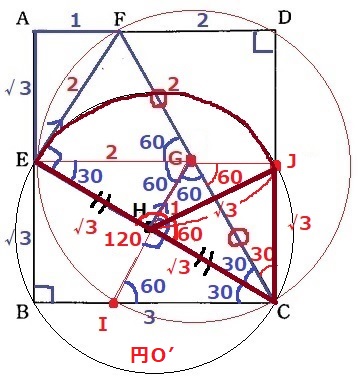
半径√３ｃｍ中心角120°の扇形と、１辺が√３ｃｍの正三角形となる。
正三角形の高さは１：２：√３から、√３×√３/２＝３/２ｃｍ
よって、√３×√３×π×120/360＋√３×３/２×１/２＝π＋３√３/４ｃｍ²

したがって、２/３π＋（π＋３√３/４）
＝５/３π＋３√３/４ｃｍ²
*しんどかった:( ´ω` ):
角度や辺の情報がごちゃごちゃしましたが、途中の説明は他にもいろいろあります。
ポイントは扇形と正方形の交点Ｉ・Ｊがどのような位置にあるのかを見極めることでしょうか。
中心をＧとする円Ｏの弧か、中心をＨとする円Ｏ’の弧か。
いたるところにある１：２：√３の直角三角形を活用する。
鮮やかな解法をついた方は、ぜひ下のコメント欄かお問い合わせよりお知らせ願います<(_ _)>

大問５（関数）

①
うしろの設問の前提となるので必答。
ｙ＝４/３ｘ²にｘ＝５/４を代入。
ｙ＝４/３×（５/４）²＝25/12

ｙ＝ａｘ²にグラフでｘの値がｐ→ｑに増加したときに変化の割合はａ（ｐ+ｑ）
ａ（－３＋０）＝－１
ａ＝１/３
点Ａのｙ座標…25/12、ａ＝１/３

②
解答では途中式も記述する。
Ｃのｘ座標をｔとする。Ｃ（ｔ、１/３ｔ²）
ｔ＋１/３ｔ²＝10/３
ｔ²＋３ｔ－10
＝（ｔ＋５）（ｔ－２）＝０
ｔ＞０だから、ｔ＝２
ｙ＝１/３×２²＝４/３
Ｃ（２、４/３）

③（１）

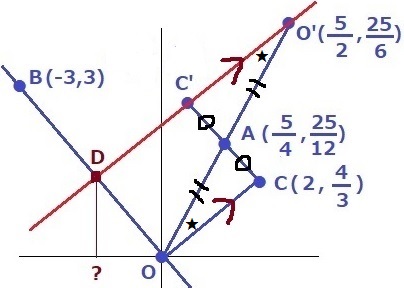
△ＯＡＣ＝△Ｏ’ＡＣ’、対応する角より∠ＡＯＣ＝∠ＡＯ’Ｃ’
錯角が等しく、ＯＣ//Ｃ’Ｏ’
ＯＣの傾きは、４/３÷２＝２/３
→Ｃ’Ｏ’の傾きも２/３。

対応する辺よりＯＡ＝ＡＯ’だから、
Ｏ’の座標はＡ座標を２倍した（５/２、25/６）。
Ｃ’Ｏ’は傾き２/３でＯ’（５/２、25/６）を通る直線なので、
25/６＝２/３×５/２＋ｂ
ｂ＝５/２
Ｃ’Ｏ’；ｙ＝２/３ｘ＋５/２

Ｂ（－３、３）→ＢＯ；ｙ＝－ｘ
Ｄはｙ＝２/３ｘ＋５/２とｙ＝－ｘの交点。
２/３ｘ＋５/２＝－ｘ
ｘ＝－３/２

（２）

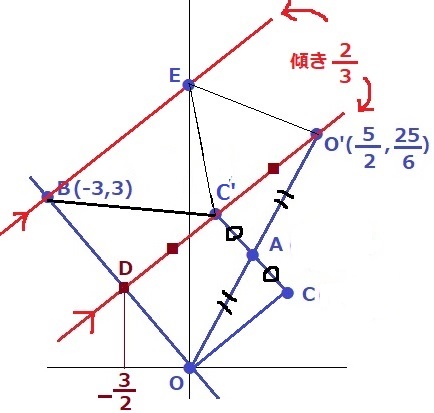
ＤＣ’とＣ’Ｏのｘ座標の差はともに２。
Ｃ’はＤＯ’の中点である。
これさえわかれば、△ＢＤＣ’と△Ｏ’Ｃ’Ｅにおいて底辺はＤＣ’＝Ｃ’Ｏ’だから、
高さが等しい→平行線！
Ｂを通る、ＤＯ’に平行な線を描き、ｙ軸との交点がＥとなる。
ＢＥの傾きは２/３。
Ｂから右に３、上に２移動してＥ（０、５）
Ｅのｙ座標は５となる。
公立高校入試解説ページに戻る