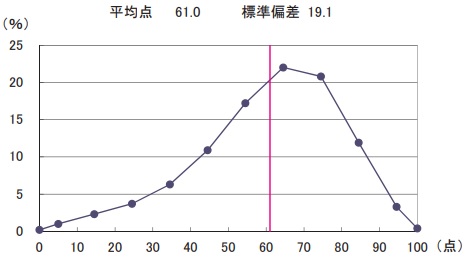
平均61.0点(前年比;-1.0点)
問題はこちら→リセマムさん
大問1(計算)-84.7%
(1) 96.9%
12-(-6)
=12+6
=18
(2) 90.3%
-52÷5/4
=-25×4/5
=-20
(3) 77.4%
3(2a+b)-5(4/5a+1/10b)
=6a+3b-4a-1/2b
=2a+5/2b
(4) 85.6%
連立方程式。加減法がやりやすいかな?
上の式を3倍か、下の式を2倍して合算。
x=4、y=-3
(5) 74.2%
(√7-√3)(√7-2√3)
=(√7)2-3√21-√3×(-2√3)
=7-3√21+6
=13-3√21
(6) 83.9%
(x+4)(x-3)-8
=x2+x-12-8
=x2+x-20
=(x+5)(x-4)
大問2(小問集合)-59.7%
(1) 76.5%
中央値(メジアン)は真ん中の値。
標本が7個であれば、(7+1)÷2=4番目の値が25.0になる。
わかっている値を昇順に並べると、
24.0<24.5<25.0<26.0<26.5<27.0
25.0を4番目にするので、aの値は25.0未満になる→ウ
(2) 69.6%

↑回転させるとトイレットペーパーみたいな感じ。
(3×3×π-2×2×π)×3=15πcm3
@パップス・ギュルダンの定理@
本問では使う必要性は乏しいのだが、回転体にはこのような定理がある。
【回転体の体積=回転する図形の面積×その重心の移動距離】
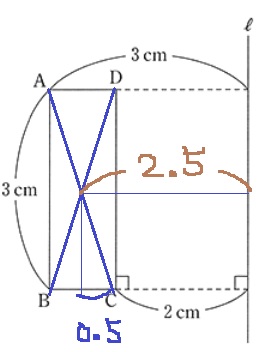
長方形ABCDの重心は対角線の交点。
移動距離は半径2.5cmの円周となる。
よって、(3×1)×(2.5×2×π)=15πcm3
回転させる図形が複雑な形をしているときに使える。
これをパップス・ギュルダンの定理といいます。
(3) 80.6%
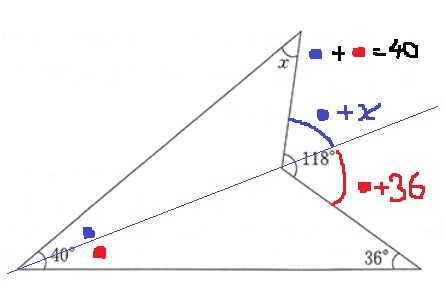
補助線をひいて、2つの三角形で外角定理。
40°を●と●にわけると、●+x+●+36=118で、
●+●=40°だから、x=118-36-40=42°
形で覚えちゃった方が早い。3つの角の和は股の角。
(4) 34.6%
△APQを想像できるか否か。
円で直角→半円の弧に対する円周角
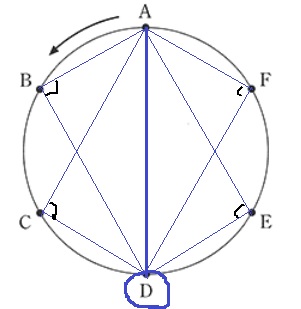
わかりやすいのはADかな?
PかQのどちらかをDにきてもらって、他方がどっかにあればいい。
・PがDにあったら、Qは残りの4通り。
・QがDにあったら、Pは残りの4通り。

Aに直角を集めるパターン。
PQがBEかCFにくればいい。
・直径BE→PがBでQがE、あるいはその逆で2通り
・直径CF→同様に2通り
計12通り
すべての場合は5×4=20通り
(カードは戻さないので、5×5=25通りではない!)
12/20=3/5
(5) 6点-37.2% 3点-3.2% 無答-21.9%
作図問題。とりやすくなってる。
AとBはともに円周上の点にくる。
円周上の2点A、Bと円の中心点Oとの距離はともに等しい。
→ABの垂直二等分線上にOがある…①
円OはAを接点として直線ℓに接する。
半径OAと接線ℓは垂直の関係。
→Aを通る直線ℓとの垂線上にOがある…②
①②の交点がOになる。
大問3(関数)-46.4%
(1) 77.6%
AとBのx座標が与えられているため、これをy=-1/8x2に放り込む。
A…y=-1/8×(-8)2=-8 A(-8、-8)
B…y=-1/8×42=-2 B(4、-2)
ABの傾きを求める。
A→Bは、右に12、上に6なので、6/12=1/2
a=1/2
(2) 49.4%
2点の座標が判明しているので、素直に三平方を使う。
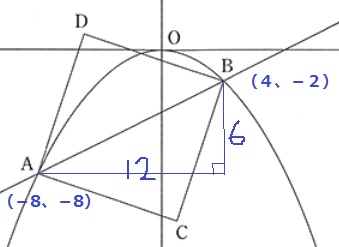
AB2=122+62=180
AB=6√5cm
(3) 12.3%!
前問で正方形の対角線がわかっている。
正方形の面積=対角線×対角線÷2
正方形ACBD=6√5×6√5÷2=90cm2
y=1/2x-4の切片をQとすると…
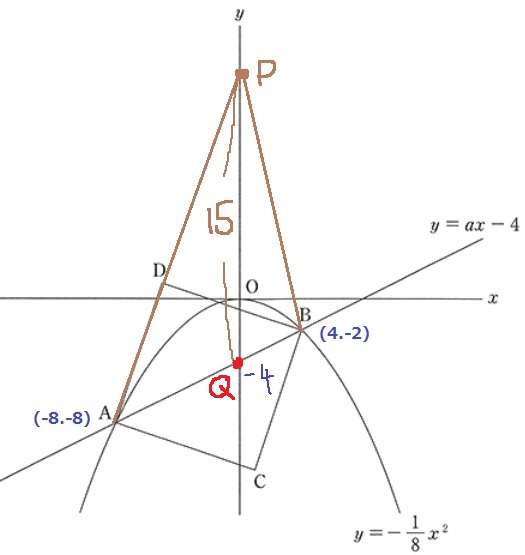
PQを底辺とし、高さは左右の合計で、4-(-8)=12cm
PQ…90×2÷12=15cm
Pのy座標は、15-4=11
比較的難しくないので、上位校狙いの生徒は落とせない。
大問4(図形)-53.0%
(1)
△BCD∽△BGFの証明。
誘導に従えば、正解できるはず。
円周角をつかって、2角が等しいことを指摘する。
a…ア 91.9% b…エ 93.1%
c…6点-24.7%! 3点-6.7% 無答-43.4%!
FE=FGを証明したいので、これらを1辺とする△BFEと△BFGに注目する。
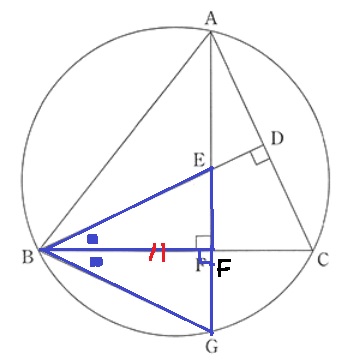
先ほどの∽から、2つの角●が等しい。
直角も等しい。共通辺→一辺両端角の相等
頂角(∠EBG)の二等分線が底辺EGと垂直の関係にあるので、
△BGEは二等辺だとわかる。
(2) 2.4%!!
情報が少ないので、前問のFE=FGを用いる。

AE:EF=2:1
AF=BFなので、BF=3となり、前問からFG=1となる。

△AFCと△BFGに着目すると、
円周角やら対頂角やらで角度が等しく、
AF=BFから一辺両端角相等で合同。
FC=1
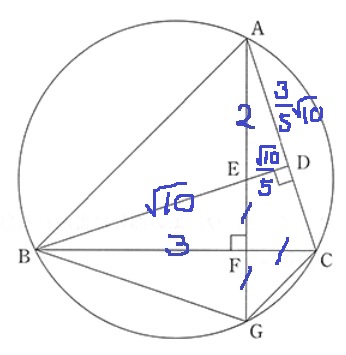
△EBFで三平方。BE=√10
△EBF∽△EAD(円周角やら対頂角やら)なので、
ED=1×2/√10=√10/5
AD=ED×3=√10/5×3=3√10/5
△AED=√10/5×3√10/5=6/5

四角形ABGCの面積は楽に求めることができる。
BCとAGが直交なので、4×4=16
よって、△AED:四角形ABGC=6/5:16=3:40
@余談@
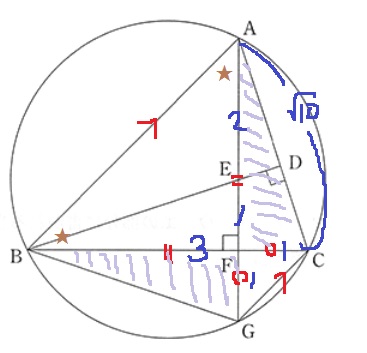
四角形ABGCの対角線が直交して、△ABFが直角二等辺であることから、
勘の鋭い人は四角形ABGCは等脚台形で、BA//GCと気付けたかもしれない。
(円周角定理で∠ABC=∠AGC。∠AGC=∠GABで錯角が等しいから)
斜めで割ると左右対称になるので、△BFGと△AFCは合同になる。
四角形ABGCを⑯として、△ABF(⑨)と△CGF(①)をひいて÷2すると、
△AFC=③となる。
斜辺の比から、△AFC:△ADE=√102:22=5:2なので、
△ADE=③×2/5=○6/5
先ほどと同じ値になる。
大問5(規則)-51.2%
(1) 86.3%
あともう少し手を伸ばせば届くので、自力で書いてみよう。
(3枚目)11、12…(4枚目)13、14、15…
14+15=29
(2) 62.3%
カードは4つずつ数字が書かれる。
58÷4=14…2
〔14枚と2個〕なので、15枚目のイとなる。
(3)① 66.1%
エのところに着目すると、
4、8、12…の数列。
n番目は4nになる。
素直を過ぎて逆にこわいね(;`ω´)
③ 10.9%!

これも書いてみる。
(8n-3)(8n+3)
=64n2-9=5175
64n2=5184
n2=81
n=9
n枚目のアは4n-3なので、
4×9-3=33
2019年度(千葉)前期
数学…平均54.5点 社会…平均56.6点 理科…平均60.6点
英語…平均53.6点 国語…平均54.2点
2019年度(千葉)後期
社会…平均65.8点 理科…平均61.6点 英語…平均61.9点 国語…平均59.2点
その他は下記リンクの目次からどうぞです。




コメント