平均27.5点（前年比；－1.4点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
８×（－７）
＝－56
（２）
４/５ｘ－２/３ｘ
＝２/15ｘ
（３）
15ｘｙ÷５ｘ
＝３ｙ
（４）
５（２ａ＋ｂ）－２（３ａ＋４ｂ）
＝10ａ＋５ｂ－６ａ－８ｂ
＝４ａ－３ｂ
（５）
（√３＋２√７）（２√３－√７）
＝６－√21＋４√21－14
＝－８＋３√21
（６）
ａ＝ｘｙ＝－２×８＝－16
ｙ＝－16/ｘ
（７）
２ｘ2＋５ｘ－２＝０
解の公式を適用して、
ｘ＝（－５±√41）/４
（８）
累積相対度数は、その階級以下の度数の合計の割合。
0.80－0.65＝0.15
０≦ウ≦0.15
ウ＝0.15のとき、20人×0.15＝３人
０≦ア≦３
ア＝０、１、２、３
大問２（小問集合２）
（１）①
18人の中央値（第２四分位数；Ｑ2）は９番目と10番目の平均。
19ｍ
②
第１四分位数は下位９個の中央値（下から５番目）で15ｍ。
第３四分位数は上位９個の中央値（上から５番目）で23ｍ。
最小値は８ｍ、最大値は35ｍ。
③ⅰ
第１四分位数はＡが14ｍ、Ｂが15ｍ。
イ
ⅱ
図１からＢの27ｍ以上は３人とわかるが、
Ａの27ｍは第３四分位数と最大値のあいだで詳細不明。
具体的にいうと、Ａの上から５番目は23ｍで１番目は38ｍ。
２～４番目はわからず、Ａの27ｍ以上は１～４人のいずれか。
ウ
（２）①
●まどか●
ｘ＋ｙ＝1200
1200ｍは家から駅までの道のりだから、ｘは歩いた道のり、ｙは走った道のり。
２つ目は時間で等式を立てる。
ｘ/50＋ｙ/90＝20
●かずと●
まどかがアだから、かずとはイ。
ｘは歩いた時間、ｙは走った時間。
１つ目は時間で等式→ｘ＋ｙ＝20
２つ目は道のりで等式→50ｘ＋90ｙ＝1200
Ａ…ア、Ｂ…ケ、Ｃ…イ、Ｄ…ウ
②
前問の連立を解く。
●まどか●
ｘ＋ｙ＝1200 …①
ｘ/50＋ｙ/90＝20 ←これを450倍
９ｘ＋５ｙ＝9000 …②
①、②を解くと、ｘ＝750、ｙ＝450
●かずと●
ｘ＋ｙ＝20 …①
50ｘ＋90ｙ＝1200 …②
①、②を解くと、ｘ＝15、ｙ＝５
これは時間なので、速さをかけて道のりにする。
50×15＝750ｍ、90×５＝450ｍ
歩いた道のり…750ｍ 走った道のり…450ｍ
（３）①
ａが平方数であれば、√ａが整数になる。
ａ＝１、４、９の３通り
確率は３/10。
②
独特な雰囲気がする。
12/ａが自然数になる→ａは12の約数。
【ａ＝１、２、３、４、６、12】の６個。
確率を１/２にするにはｎまでの自然数のうち、
半分は12の約数で、残りの半分は12の約数ではない。
分子の約数の個数に注目する。
約数の個数を２倍したｎまでに、該当する約数の個数が維持できればいい。
約数１個の場合、ｎ＝１×２＝２
２までの約数は１、２で２個だから×。
約数２個の場合、ｎ＝２×２＝４
４までの約数は１、２、３、４の４個だから×。
約数３個の場合、ｎ＝３×２＝６
約数は１、２、３、４、６の５個だから×。
約数４個の場合、ｎ＝４×２＝８
約数は５個だから×。
約数が５個の場合、ｎ＝５×２＝10
約数は５個のままだから確率は１/２。
約数が６個の場合、ｎ＝６×２＝12
約数は１、２、３、４、６、12の６個のままだから確率は１/２。
したがって、ｎ＝10、12
大問３（関数）
（１）
ｙ＝１/４ｘ2にｘ＝－２を代入。
ｙ＝１/４×（－２）2＝１
Ａ（－２、１）
（２）
Ａ（－２、１）⇒Ｂ（４、４）
右に６、上に３だから、傾きは３/６＝１/２
Ａから右に２、上に１移動して、切片は１＋１＝２
ｙ＝１/２ｘ＋２
（３）①
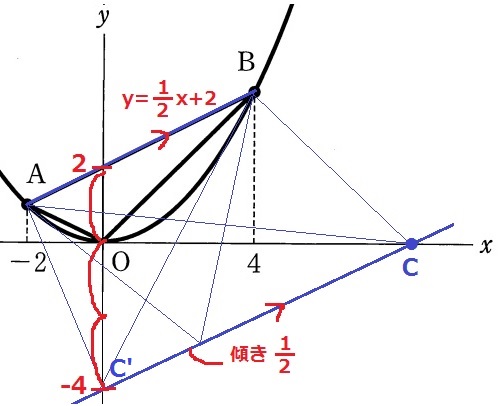
△ＯＡＢ：△ＡＢＣ＝１：３
底辺ＡＢが共通なので、高さの比が１：３になる。
ＡＢからＯまでの距離の３倍離れ、かつｘ軸上にある点がＣ。
ｙ軸上に注目しよう。
ＡＢの切片は２。
切片から６離れたｙ軸上の点をＣ’とすると、△ＡＢＣ’の面積は△ＯＡＢの３倍。
⇒切片が－４である傾き１/２の直線をひき、等積変形でＣ’をｘ軸上に移動させる。
（０、－４）から上に４、右に８移動してＣ（８、０）。
②
ＡとＢから垂線をおろし、ｘ軸との交点をそれぞれＥ・Ｆとする。
●＋×＝90°で角度を調査。２角相等により、△ＡＥＤ∽△ＤＦＢ。
Ｄのｘ座標をｔとする。
ＡＥ：ＥＤ＝ＤＦ：ＦＢ
１：ｔ＋２＝４－ｔ：４
内項と外項の積で、（ｔ＋２）（４－ｔ）＝４
ｔ2－２ｔ－４＝０
解の公式を適用。
ｔ＞０より、ｔ＝１＋√５
Ｄ（１＋√５、０）
大問４（空間図形&作図）
（１）①
直方体全体の体積を１とする。
三角柱ＡＢＤ—ＥＦＨの体積は１/２。
三角錐Ｄ—ＥＦＨの体積は÷３して１/６。
三角錐Ｄ—ＥＦＨと三角錐Ｉ—ＥＦＨの体積比は、１/６：１/９＝③：②
体積が２/３倍だから、高さも２/３倍。
６×２/３＝４ｃｍ
②
ＥＩを対角線とする直方体を作成。
１辺がａ、ｂ、ｃの直方体の対角線→√（ａ2＋ｂ2＋ｃ2）
前問より三角錐の高さは直方体の２/３倍だったので、ＤＩ：ＩＦ＝①：②
これを活用して２ｃｍと３ｃｍをだす。
ＥＩ＝√（２2＋３2＋４2）＝√29ｃｍ
（２）
①∠ＯＢＤ＝90°だから、Ｂを通る垂線。
②∠ＣＡＯが弧ＢＣに対する円周角であることに気がつきたい。
この中心角にあたる∠ＣＯＢは２倍の大きさで、
∠ＣＯＢを２等分すると∠ＤＯＢ＝∠ＣＡＯとなる。
大問５（平面図形）
（１）
△ＡＩＨ∽△ＨＩＧの証明。
誘導に従えばいい。
∠ＡＩＨ＝∠ＨＩＧが共通角（アルファベットは対応する順に並べる）。
弧ＡＥに対する円周角とＦＨ//ＥＣの錯角より、∠ＡＨＩ＝∠ＡＣＥ＝∠ＨＧＩ
２角が等しいので∽。
ア…∠ＡＩＨ＝∠ＨＩＧ、イ…∠ＡＣＥ、ウ…２組の角
（２）
△ＡＦＧ≡△ＣＥＤの証明。
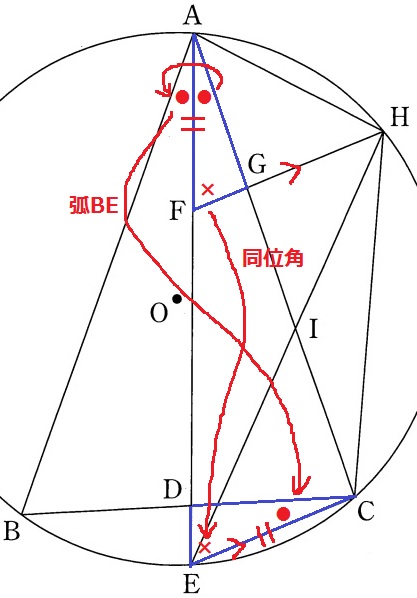
仮定より、ＡＦ＝ＣＥ
等辺の情報はこれしかないから、この両端角に目をつける。
ＦＨ//ＥＣの同位角で、∠ＡＦＧ＝∠ＣＥＤ（×）
仮定の二等分線と弧ＢＥに対する円周角より、∠ＦＡＧ＝∠ＥＣＤ（●）
１辺と両端角が等しいので合同。
（３）①
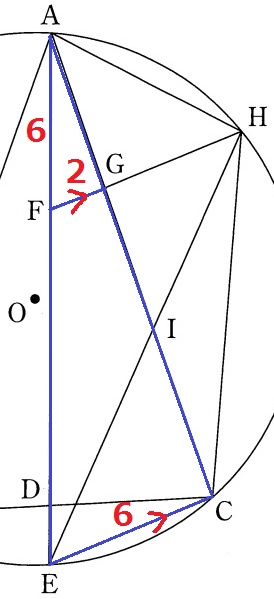
△ＡＦＧ∽△ＡＥＣより、ＦＥ＝６×４/２＝12ｃｍ
②
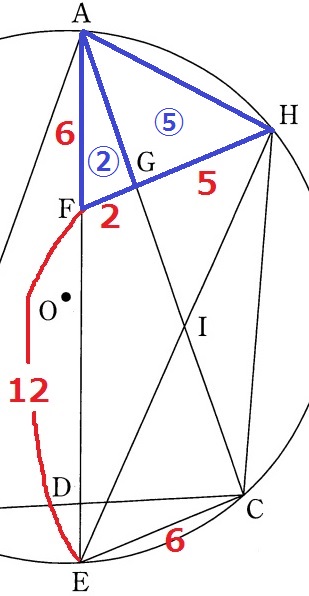
ＦＧ：ＧＨ＝２：５
△ＡＦＧの面積を②とすると、△ＡＧＨは⑤。
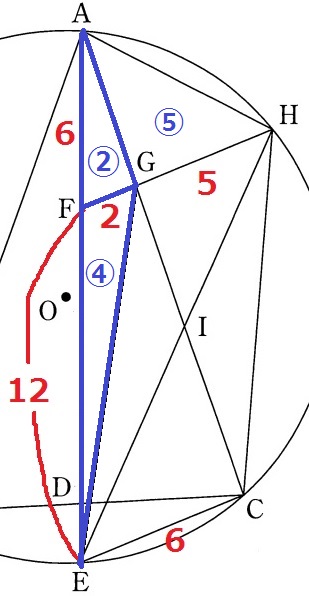
先ほどＦＥの長さを求めたので、これを有効利用できないか。
ＧＥに補助線。△ＦＥＧ＝②×12/６＝④
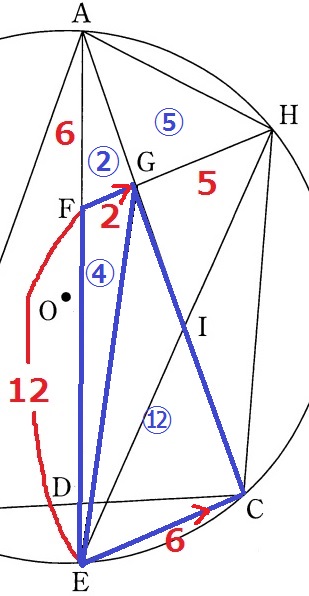
台形ＦＥＣＧの上底と下底から、△ＧＥＣ＝④×６/２＝⑫
△ＩＨＧ∽△ＩＥＣで、ＧＩ：ＩＣ＝５：６
△ＩＥＣ＝⑫×６/11＝〇72/11
△ＩＥＣ：△ＡＧＨ＝〇72/11：⑤＝72：55
大問１
配点13点。
オール基本問題なので迅速かつ正確にあてにいきたい。
（８）ウの範囲を不等号であらわしてみる。
大問２
（１）③ⅱ27ｍは第３四分位数～最大値のヒゲの中にあるので詳細は不明。
（２）かずとの方が連立は解きやすいかもしれないが、求めたいものが文字ではない。
（３）②正答率悪いと思う。
ａが12の約数であるとつかむ。
ｎが13以上になると確率は減っていくので、わからなかったら１個ずつ調べるのも手。
大問３
（３）①ＣはＯより３倍離れるが、ＡＢは斜めに傾いている。
ｙ軸上で判断するとやりやすい。
②直角三角形の●＋×＝90°。この角度調査は頻出だが形式がやや特殊である。
大問４
（１）①不要な部分を削っていく。底面共通だと高さの比が体積比。
（２）等しい同位角からＡＣ//ＯＤとなるが、半円があるから円周角と中心角を活用する。
大問５
（３）②既知の情報が上に偏るので△ＡＧＨから出発する。
前問のＦＥをどう使うか。台形ＦＥＣＧを分割すると見えやすい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント