平均22.6点(50点満点)
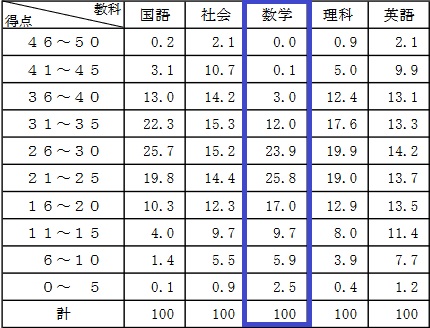
問題はこちら→リセマムさん
大問1(計算)
(1)① 98.4%
(-9)×(-5)
=45
② 93.4%
(-3/4)+2/5
=-7/20
③ 83.4%
(-4x2y)÷x2×2y
=-8y2
④ 82.7%
18/√6+√24
=3√6+2√6
=5√6
(2) 77.3%(部分正答0.2%)
反比例:y=a/x
積が48で一定。
□=48÷6=8
大問2(小問集合)
(1) 79.8%(部分正答0.2%)
x2-8x-20
=(x+2)(x-10)
(2) 79.3%(部分正答1.4%)
『100枚では足りない』ので、配る折り紙の数は100を超える。
4a+3b>100
(3) 89.3%
グラフの傾きが急であるほど、給水管の本数が多い。
傾きの度合いは、C>A>B=D
エ
(4) 32.0%!
円錐Bの底面の半径をr、高さをhとおく。
円錐Bの体積:r×r×π×h×1/3=πr2h/3
円柱Aの体積:2r×2r×π×h=4πr2h
円柱A:円錐B=4πr2h:πr3h/3=12:1
円柱Aの体積は円錐Bの12倍
(5) 54.1%(部分正答6.8%)
対称の軸からAとPは等距離にある。
対称の軸上の点(BとC)からも等距離にある。
BA、CAの距離をとり、Aと反対側にできる交点がPとなる。
もしくは、対応するAとPを結んだ線分はBCに直交するので、
Aを通る、BCに垂直な線分を作図し、BC~Aの距離を反対側に持ってきてもOK。
大問3(確率・データの活用)
(1)① 79.1%
教科書でお馴染みなので、結果を覚えていた人がいたかも。
和が7→(1、6)(6、1)(2、5)(5、2)(3、4)(4、3)
6通り
② 40.2%(部分正答2.0%)
2→(1、1)
3→(1、2)(2、1)
5→(1、4)(4、1)(2、3)(3、2)
7→前問より6通り
11→(5、6)(6、5)
15/36=5/12
(2)① 70.5%
最頻値(モード)は最も度数の多い階級。
階級値は階級の真ん中の値。
210と220の間の数⇒215cm
② 39.3%(部分正答28.0%)
『220cm以上の生徒の割合』⇒220cm以上の相対度数を求める。
1組男子…6÷16=0.375
3学年男子…33÷75=0.44
1組男子の方が220cm以上の相対度数が小さいので、
1組に記録の高い生徒が多いとはいえない。
イ
大問4(方程式)
6.1%!!(部分正答10.7%)
説明込み。
単品ノート…x冊、単品消しゴム…y個
セットAのノート…3x-1冊
セットBの消しゴム…2y個
セットAでノートは1冊なので、セットAで売れたノートの冊数とセットAの売れたセット数が同じになる。
すなわち、セットAは3x-1セット売れた。
同様に、セットBでは消しゴムは1個なので、セットBで売れた消しゴムの個数と同じ、
セットBは2yセットが売れたことになる。
『ノートは全部で41冊売れた』…単品+セットA+セットBのノートの合計が41冊。
x+(3x-1)+3×2y=41
2x+3y=21…①
『売り上げの合計は5640円』…4つの商品すべての合計。
120x+60y+160(3x-1)+370×2y=5640
3x+4y=29…②
①、②より、x=3、y=5
単品ノート…3冊、単品消しゴム…5個
大問5(平面図形)
(1) 15.5%!(部分正答17.3%)
∠AFD=∠ADFの証明。
角度の問題だが、わざわざCD=EFとあるので、
ここを1辺とする三角形の合同を経由する。
〔公式解答:例2〕
△ACFと△AEDに注目。

仮定より、CD=EF
CB//AEで錯角が等しい。(∠ECB=CEA)
すると、△ACEが二等辺となる。
AC=AE
2辺と間の角が等しい⇒△ACF≡△AED
対応する辺であるAD=AFとなる。
△ADFが二等辺だから、底角の∠AFD=∠ADFが導ける。
〔公式解答:例1〕
△ACFと△AEDに注目。

CF=CD+DF
ED=EF+FD
ここから、CF=ED
あとは先ほどと同様の流れ。
(2) 8.0%!!
等角をどこまで認定できるか。

出発は∠ACBの二等分線から。
∠ECA=∠ECB=●とおいて調査する。
∠FCA=∠FAEは接弦定理。
平行線から錯角、前問の合同。
さらに、外角定理から∠CFA=●●、円周角へ結ぶ。
すると、△ABCの内角が●×5となる。
∠ABC=180×2/5=72°
@別解@

∠ACB●●を錯角で降ろし、接弦定理で∠ABCへ。
どのみち接弦定理は必要かと思われる。
大問6(関数)
(1) 53.2%
y=x2に代入して座標を求める。
A(-3、9)⇒B(-1、1)
右に2、下に-8だから、傾きは-4
(2)① 34.3%(部分正答1.6%)
C(2、4)
直線ℓの傾きは前問で-4と求めたので、
直線mはC(2、4)を通り、傾き-4
4=2×(-4)+b
b=12
m:y=-4x+12
Dはこの式の切片だから、(0、12)

欲しい情報は、BCの切片。
BCの傾きは、右に3、上に3で1
切片はBから右1、上1なので、(0、2)
△BCD=(12-2)×3÷2=15
② 0.7%!!!
AB//DCで、A-B間とD-C間のx座標は各々2ずつ離れている。

1組の辺の長さが等しく、かつ平行なので、四角形ABCDは平行四辺形となる。
(AD、BCの傾きは共に1で平行)
平行四辺形ABCDの面積は30
四角形BPCQの面積は、30×1/5=6になればいい。
Pのx座標をtとするので、P(t、t2)
Qは前問で使った直線mに代入。Q(t、-4t+12)

4つの座標の位置を確認。外側に長方形を作成する。
四角形BPCQが6なので、長方形の面積は12となる。
長方形の横は2、縦はQのy座標-Pのy座標から-t2-4t+12
3(-t2-4t+12)=12
-3t2-12t+24=0
t2+4t-8=0
因数分解ができないので、解の公式。
t=-2±2√3
0<t<2より、t=-2+2√3
大問7(空間図形)
(1) 69.5%
AB=12、BM=6
△ABMで三平方(1:2:√3)→AM=6√3
(2)① 8.2%!!
新しい点が次々と追加されて、頭が混乱しやすい。
AEとEDの和が最も小さくなる→展開図に直して直線。
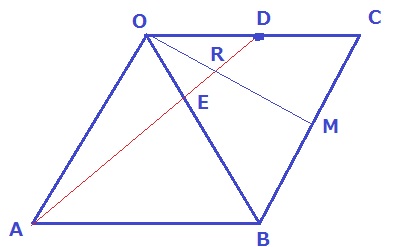
↑位置関係はこんな感じ。

Dを通る、OAに平行な線分を作成。OMとの交点をNとする。
△ODN∽△OCMより、
DN=6÷2=3
△OAR∽△DNRより、
OR:RN=OA:DN=12:3=4:1
NはOMの中点⇒OR:RM=4:6=2:3
② 0.0%!!!
三角錐QBPCを作図する。

最終的に体積を求めるので、全体(正三角錐OABC)からの割合を出す。
三角錐QPBCの底面積を△PBCとする。
△ABC:△PBCは底辺BCを共通とするので、2つの面積比は高さの比9:4と等しい。
三角錐QPBCの高さの比となる、OQ:QPが知りたい。
そこでQの位置を確認する。Qは面ADEとOPとの交点。
ここでRの位置に注目しよう。
Rも面ADE上にあるので、同じ面にAとQとRがある。
また、QはOP上にあり、OPは△OAM上にある。
RはOM上にあるので、QとRは△OAM上にある。
ということは、面ADEと△OAMが交差する一直線上にA・Q・Rがある。
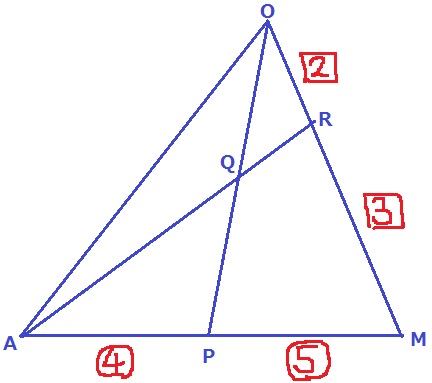
△OAMで考える。
メネラウスの定理から、
OQ/QP×4/9×3/2=1
OQ:QP=3:2
全体の体積(正三角錐OABC)を求める。
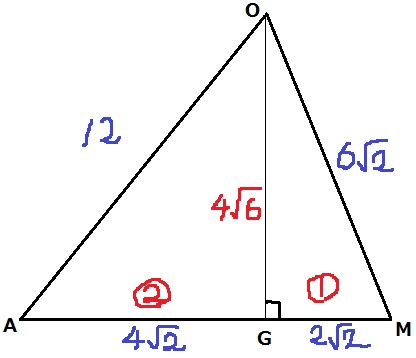
高さが厄介(;´Д`)
Oから△ABC(底面)に向けて垂線をひき、交点をGとおく。
GM=xとおいて、AG=6√2-x。
三平方で、AO2-AG2=OM2-GM2としてもよいが、
正三角錐の場合はGが底面の重心を通るので、AG:GM=2:1
GM=2√2
△OGMで三平方→OG=4√6
三角錐QPBC=12×6√2×1/2×4√6×1/3(OABC)×5/9(底面積)×2/5(高さ)
=32√2cm3



コメント