2022年度　群馬県公立高校入試問題過去問【数学】解説

平均57.7点（前年比；＋9.7点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①
３－７
＝－４

②
３ｘ＋２（ｘ－１）
＝３ｘ＋２ｘ－２
＝５ｘ－２

③
12ａｂ³÷４ａｂ
＝３ｂ²

（２）①
４ｘ＋５＝ｘ－１
３ｘ＝－６
ｘ＝－２

②
ｘ²－３ｘ＋１＝０
解の公式を適用して、
ｘ＝（３±√５）/２

（３）
ｘ²－16ｙ²
＝（ｘ＋４ｙ）（ｘ－４ｙ）

（４）
（２ａ＋ｂ）－（ａ＋４ｂ）
＝２ａ＋ｂ－ａ－４ｂ
＝ａ－３ｂ　←ここで代入
＝３－３×１/３
＝２

（５）

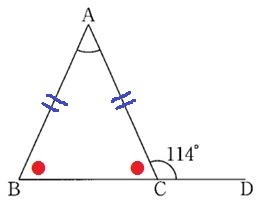
∠ＡＢＣ＝∠ＡＣＢ＝180－114＝66°
△ＡＢＣで外角定理→∠ＢＡＣ＝114－66＝48°

（６）
答案では過程も記述する。
ｙ＝ａｘ²に（ｘ、ｙ）＝（－２、８）を代入。
８＝４ａ
ａ＝２
ｙ＝２ｘ²にｘ＝３を代入して、ｙ＝18

（７）
全体は、３×３＝９通り
１回だけ赤は（赤、白）（赤、青）（白、赤）（青、赤）の４通り。
確率は４/９。

（８）

三角錐はウ。

（９）
ア：Ａ中で15ｍ未満の相対度数の合計は、０＋０+0.20＝0.20
　30×0.20＝６人×
イ：相対度数はともに0.30だが、全数が30人と40人で違うから人数は違う。×
ウ：25ｍ以上の割合はＡが0.20、Ｂが0.35でＢの方が大きい。〇
エ：30～35ｍの階級のなかで、どちらが最大値を叩き出したかはわからない。×
ウ

大問２（整数）

（１）
①５は自然数。自然数は正の整数。【１・２・３…】
②√３は無理数。整数の分数で表せる数が有理数、表せないと無理数。
③３/11は整数の分数だから有理数。
①…ウ、②…エ、③…ア

（２）
ア：逆数はある数との積が１になる数。２の逆数は１/２で自然数ではない。×
　１以外の逆数は自然数にならない。
イ：数直線を思い浮かべよう。大きい整数と小さい整数の差は正の整数（自然数）である。
　これは、もとの整数が負の数でも０をまたぐ場合でも同様である。〇
ウ：（ｘ＋３）（ｘ－２）＝０の解はｘ＝－３、２。（ｘ－５）²＝０はｘ＝５。
　解が分数の場合もある。×
　解の公式でいえば、根号の中のｂ²－４ａｃの値が平方数であれば解は有理数になる。
エ：独特な雰囲気があるが、有理数も無理数も数直線上の点で表せる。〇
　高校で習う虚数は数直線では表せない。
イ・エ

大問３（平面図形）

（１）同一円周上にある。

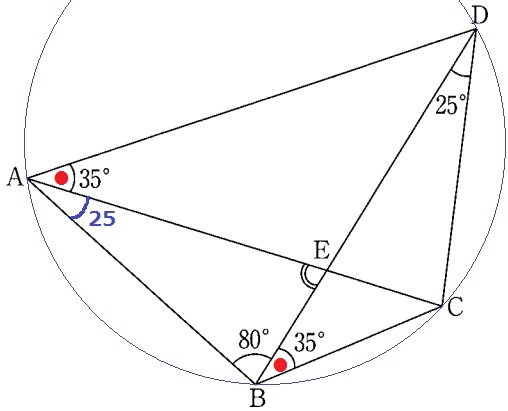
*２点Ａ、Ｂが直線ＣＤについて同じ側にあり、∠ＣＡＤ＝∠ＣＢＤだから、
円周角定理の逆によって、４点Ａ、Ｂ、Ｃ、Ｄは同一円周上にある。

（２）
弧ＢＣに対する円周角で、∠ＢＡＣ＝25°
△ＡＢＥの内角から、∠ＡＥＢ＝180－（25＋80）＝75°

大問４（平面図形２）

（１）
角の二等分線の作図法の原理。
説明は問題文の言い回しをまねればいい。

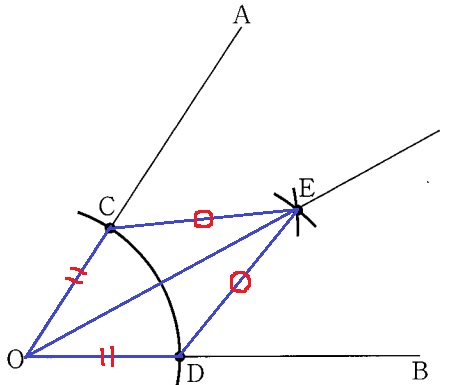
手順Ⅰより、ＯＣ＝ＯＤ
手順Ⅱより、ＣＥ＝ＤＥ
共通辺ＯＥ。
３辺が等しいから、△ＯＣＥ＝△ＯＤＥ

＠つづき＠
対応する角は等しいので、∠ＣＯＥ＝∠ＤＯＥ
半直線ＯＥは∠ＡＯＢの二等分線となる。

（２）
前問の角の二等分線を使う。

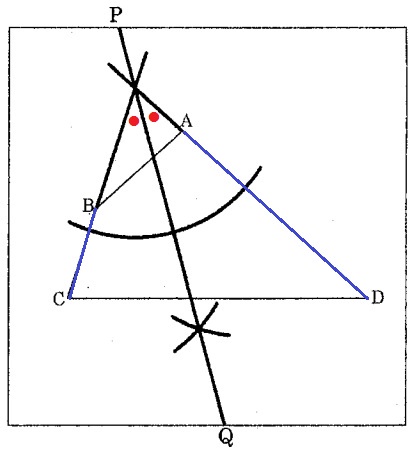
折り目の問題は垂直二等分線が定番だが、ＡとＢ、ＣとＤは対応する点ではない。
そこで、ＡＤとＢＣを延長し、２直線がなす角の二等分線を作図する。
二等分線は２直線からの距離が等しく、これを折り目とするとＢＣがＡＤにピッタリ重なる。
『折り紙にできる折り目ＰＱ』なので、二等分線を正方形の折り紙の端まで伸ばすこと！

大問５（規則）

（１）

魔方陣の考えを用いる。
１つの固まりは、【１・３・５…】と連続する奇数で増えている。
４番目の外側は、７×４＝28個

（２）
ｎ番目の１つの固まりは、ｎ番目の奇数だから２ｎ－１個。
これが４つなので、４×（２ｎ－１）＝８ｎ－４個

（３）①
答案では求める過程も記述する。
中の碁石は取り除くので、黒と白はそれぞれ１周ずつしかない。

ｎ番目の正方形で300個の石を使い切ったとすると、
前問の式より、８ｎ－４＝300
ｎ＝38
38番目

②
38は偶数。
偶数番目は白が外側にくる。
つまり、300個使い切ったのは白で、残ったのは黒。

黒は37番目だから、８×37－４＝292個
余った石は、300－292＝８個
黒、８個

＠余談＠
ｎ番目は８ｎ－４個。
ｎ－１番目は８（ｎ－１）－４＝８ｎ－12個。
（８ｎ－４）－（８ｎ－12）＝８だから、使い切った白の１個手前の黒は８個残っている。

魔方陣で考えれば、１つの固まりの個数は連続する奇数だったので、
１つ内側の固まりは－２、これが４つで－８⇒８個差。

大問６（数量変化）

（１）

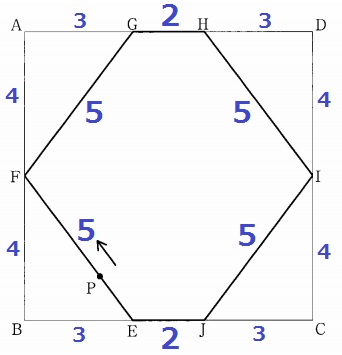
３：４：５の直角三角形から斜めは５ｃｍ。
Ｅ～Ｊまでは、５×４＋２＝22ｃｍ
Ｐは毎秒１ｃｍなので22秒後。

（２）①

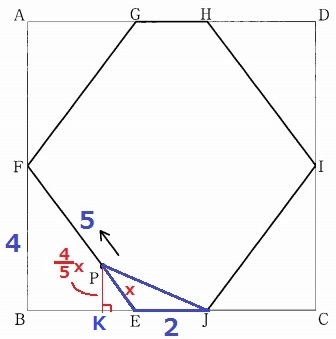
△ＥＪＰの底辺はＥＪ＝２ｃｍで固定。
高さだけが長くなるので、面積は比例で増加する。

Ｐの垂線の足をＫとすると、高さはＰＫにあたる。
△ＦＥＢ∽△ＰＥＫより、ＰＥ：ＰＫ＝５：４
Ｐが進んだ距離ＰＥがｘｃｍだから、ＰＫ＝４/５ｘｃｍ
したがって、△ＥＪＰの面積ｙ＝２×４/５ｘ÷２＝４/５ｘ
ｙ＝４/５ｘ

②

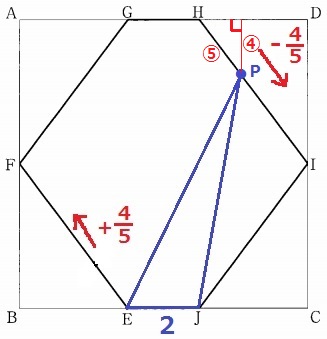
底辺はＥＪで固定。高さだけが減少するので一次関数。
ＥＦ上では面積の変化率（＝高さの変化率）が４/５であった。
ＨＩ上ではＰの移動距離ＨＰの４/５倍が高さの減少分に相当する。
⇒変化率（傾き）は－４/５

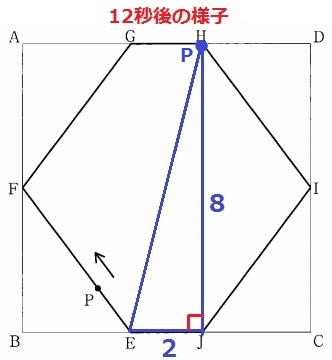
ＰがＨに着く12秒後の△ＥＪＰの面積は、２×８÷２＝８ｃｍ²

ｙ＝－４/５ｘ＋ｂに（ｘ、ｙ）＝（12、８）を代入する。
８＝－４/５×12＋ｂ
ｂ＝88/５
ｙ＝－４/５ｘ＋88/５

（３）
△ＥＪＰと△ＥＪＱは底辺がＥＪで共通。
高さが等しいときに面積は等しくなる。
⇒１回目はＱがＰに追いついたとき。

Ｑが出発する３秒後、ＰとＱは３ｃｍ離れている。
１秒あたり１ｃｍずつ差が縮まっていくので、
３÷１＝３秒後、すなわち、Ｐ出発時から６秒後（ｘ＝６）である。

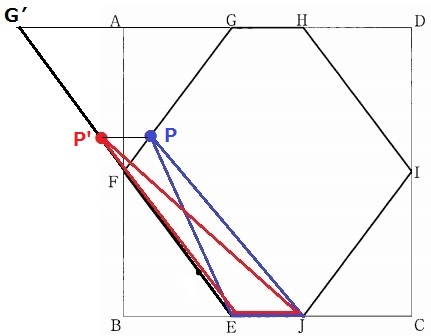
ＰはＦＧ上にあるが、高さの変化率は４/５のまま。
（上図のようにＧ’Ｅを直線にした場合と同様）
ｙ＝４/５ｘにｘ＝６を代入して、
ｙ＝４/５×６＝24/５

２回目はＱがＨを過ぎ、△ＥＪＱの高さが減少していくとき。

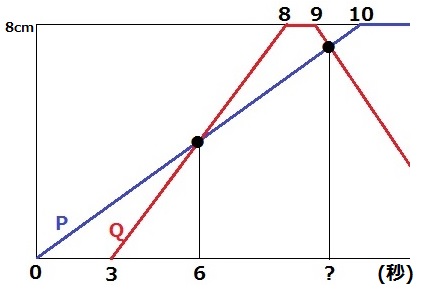
中学受験の戦法を使います(;^ω^)
ダイヤグラムを作る。横軸は秒数で、縦軸は三角形の高さ。
ＰがＧに到着するのは10秒後、ＱがＨを出発するのはＰが出発してから９秒後。

速さの比は、Ｐ：Ｑ＝１：２
時間の比は逆比で、Ｐ：Ｑ＝②：①
９～10秒後において、うえのような垂線をひくと、
この距離をＰは②、Ｑは①の時間で移動する。
③が１秒だから、交点の時間は、９＋１×①/③＝28/３秒

28/３秒後のＰはＦＧ上にある。
ｙ＝４/５ｘにｘ＝28/３を代入。
ｙ＝４/５×28/３＝112/15

ｘ＝６のとき、ｙ＝24/５
ｘ＝28/３のとき、ｙ＝112/15