2020年度　福岡県公立高校入試過去問【数学】解説

平均55.7％（前年比；＋2.6％）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）－83.6％

（１）　96.9％
８＋２×（－７）
＝８－14＝－６

（２）　89.9％
２（ａ＋４ｂ）－（５ａ＋ｂ）
＝２ａ＋８ｂ－５ａ－ｂ
＝－３ａ＋７ｂ

（３）　90.8％
√75－９/√３
＝５√３－３√３
＝２√３

（４）　92.2％
３（２ｘ－５）＝８ｘ－１
２ｘ＝－14
ｘ＝－７

（５）　77.1％
２ａ＋３ｂ＝１
２ａ＝－３ｂ＋１
ａ＝（－３ｂ＋１）/２

（６）　80.2％
ｘとｙの積が－12（ｙ＝－12/ｘ）
ｙ＝－12÷３＝－４

（７）　73.9％
ｙの値が整数となるのは、ｘの値が３の倍数のとき。
原点と（３、３）を通るような放物線を描く。

（８）　74.4％
電卓使いました。
Ａ中学校…25÷85＝0.294…≒0.29
Ｂ中学校…32÷136＝0.235…≒0.24
大きい方は0.29。

（９）　77.2％
無作為に抽出した30個のうち、印付きは２個。
印なし：印あり＝28：２＝⑭：①（全部で⑮）の割合で、
この割合は母集団も変わらないとみなす。
印付きは全部で30個だから、30×⑮/①＝450個

大問２（文字式）－52.8％

（１）　72.8％
縦の長さをｘｍとすると、横の長さは２ｘｍ
２（ｘ＋２ｘ）＝２×（縦の長さ＋横の長さ）
土地の周の長さとなる→ア

（２）方程式…48.3％、長さ…37.2％

すべての花壇を隅に寄せるのが定石。
ア：花壇の面積で等式。
（ｘ－２）（２ｘ－２）＝264
*寄せた花壇の縦と横をかけて、花壇の面積を算出。
こちらの方が式がシンプル。

イ：道の面積で等式。
ｘ×２ｘ－264＝ｘ×２＋２×２ｘ－４
*土地の面積－花壇の面積＝道の面積
右辺の－４は、重複した部分の２×２ｃｍ²

いずれかの式を解いて、ｘ＝13
土地の縦の長さ…13ｍ

大問３（確率）－63.1％

（１）　83.3％
ＡからＤに止まるには、３か７進む。
３は（１、２）だけなので７を考える。
（２、５）（３、４）

（２）　52.9％
記述式。
３が２枚あるので、公式解答のように〇の有無や３_Ａ・３_Ｂのように区別して調べる。
５枚から２枚取り出す場合の数→₅Ｃ₂＝10通り

Ａに止まるには、４か８進む。
（１、３）（１、③）（３、５）（３、⑤）の４通り。
確率は４/10＝２/５

Ｃに止まるには、２か６進む。
（１、５）（３、③）の２通り。
確率は２/10＝１/５

計算結果を比較する。
確率は２/５＞１/５なので、コマが止まりやすいのはＡ。

大問４（数量変化）－55.9％

（１）　69.4％
図１より、Ａプランでは60分で電話料金が3600円だから、3000円は60分より前。
通話時間に応じた通話料は、3000－1200＝1800円
60分までは１分40円なので、1800÷40＝45分

（２）　73.5％
ア：基本使用料はｘ＝０のときのｙの値→2300円
イ：20分までは基本使用料のみ→20分
ウ：変化の割合は、ｙの増加量/ｘの増加量
（3300－2300）/（60－20）＝25円

（３）　43.4％
記述式。

60≦ｘ≦90におけるＡプランは（60、3600）を通る。
通話料は１分あたり30円なので傾きは30→ｙ＝30ｘ＋1800
Ｃプランは（60、3900）と（90、4350）を通る。
２点を通過する直線の式を求める。
（２）ウのように変化の割合を調べると、（4350－3600）/（90－60）＝15
Ｃプランは60分を超えると、通話料は１分15円かかることになる。
座標を代入して切片を求めると、ｙ＝15ｘ＋3000

２直線の交点座標を求める。
30ｘ＋1800＝15ｘ＋3000
ｘ＝80　→80分

＠別解＠

本問は条件付きの説明問題なので使えませんが、
条件がなかったら、中学受験のように∽で解いてしまった方が早いです。

大問５（平面図形）－35.2％

（１）　85.3％
図に線を描いてみよう。

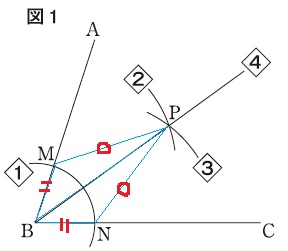
ＢＰを対称の軸とした線対称→ウ

（２）②…68.4％、③…45.3％
角の二等分線の作図の原理。
ここもワークに載っているレベルなのでこぼしたくない。
【１】からＢＭ＝ＢＮ（②）
【２】からＭＰ＝ＮＰ（③）
これと共通辺をあわせ、３辺が等しいので△ＭＢＰ≡△ＮＢＰとなる。

（３）　41.4％
△ＡＢＤ∽△ＦＡＥの証明。

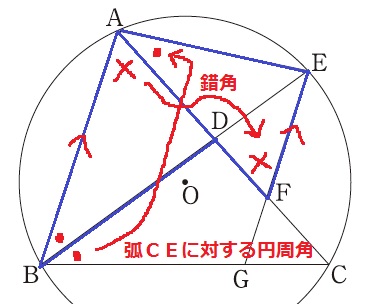
●：角の二等分線＋弧ＣＥに対する円周角
×：ＡＢ//ＥＧの錯角
２角が等しい→∽

（４）　4.2％!!
ここでひっかかる人が多いと思われる。

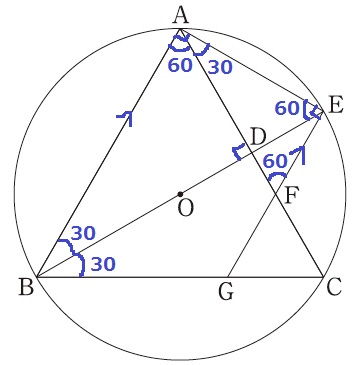
直径に対する円周角は直角なので、∠ＢＡＥ＝90°
先ほどの△ＡＢＤ∽△ＦＡＥを手がかりに対応する角を調べていくと、
∠ＢＡＤ＝60°となり、内角が30°－60°－90°の直角三角形が複数見つかる。
また、△ＡＢＥの内角も同様で、∠ＡＥＤ＝60°

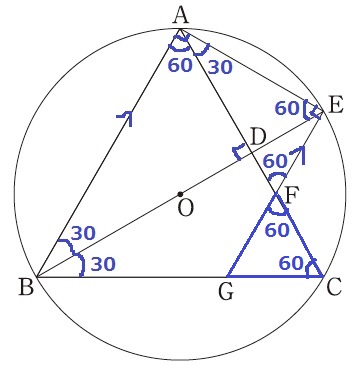
対頂角から∠ＣＦＧ＝60°
弧ＡＢに対する円周角で、∠ＦＣＧ＝60°
ここから△ＡＢＣと△ＦＧＣは正三角形となる。

△ＡＥＦの各辺を①：②：〇√３とする。
△ＡＥＢも１：２：√３なので、ＡＢを〇で示すと、〇√３×√３/１＝③
正三角形ＡＢＣの１辺は③となる。

ＦＣの長さは③－②＝①
△ＡＢＣの面積15ｃｍ²は、③×③＝【９】（【９】＝15ｃｍ²）
△ＦＧＣの面積は【１】、△ＢＤＣはＢＤが△ＡＢＣを二等分するので【4.5】
ということは、四角形ＢＧＦＤの面積は、【4.5】－【１】＝【3.5】
よって、四角形ＢＧＦＤの面積は、15×3.5/９＝35/６ｃｍ²

大問６（空間図形）－24.3％

（１）　78.0％
ア：平行×
イ：∠ＤＡＢ＝90°→垂直〇
ウ：対面で平行〇
エ：ネジレの位置→平行でもない、かつ延長しても交わらない。平行で×
ＣＤとネジレにあるのは、ＡＥ、ＢＦ、ＥＨ、ＦＧ。
イ・ウ

（２）　14.2％！

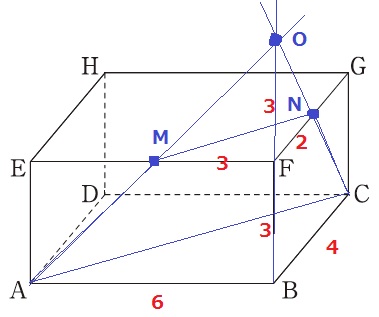
ＡＭ・ＢＦ・ＣＮを延長し、交点をＯとする。
三角錐Ｏ－ＭＦＮとＯ－ＡＢＣの辺の比は１：２なので、ＯＦ＝３ｃｍ
体積比は辺の比の３乗。
６×４÷２×６÷３×７/８＝21ｃｍ³

（３）　4.9％!!
昨年度の方がもっと複雑だった。

ＩＪを対角線とする直方体を作図。
辺の長さは、背面の１：２をうまく利用しよう！
横の辺は６ｃｍを、高さは３ｃｍを１：２に按分する。
１辺がａ、ｂ、ｃの直方体の対角線の長さ→√（ａ²＋ｂ²＋ｃ²）
ＩＪ＝√（２²＋３²＋２²）＝√17ｃｍ

正答率が３割を切る設問は５（４）６（２）（３）しかない。
上位校狙いは高得点を目指したい。
大問１
全体的に正答率が高い＝ミスが痛い。
大問２
（２）花壇の問題はよくある形式。隅に寄せるアがやりやすい。
大問３
（２）重複する３をどのように記すか。
大問４
（３）説明問題。正攻法で解いていけば条件に沿う流れになる。
大問５
（３）テクニカルな問題。１：２：√３の活用、面積比の算出も工夫する必要がある。
大問６
（３）昨年度の最後と同様、それが対角線となる直方体で終了。
公立高校入試解説ページに戻る