平均21.0点(50点満点)
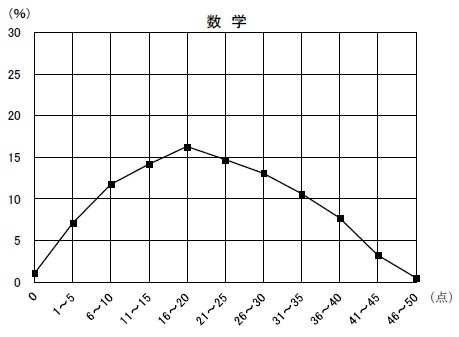
問題はこちら→リセマムさん
大問1(計算)
(1) 95.2%
-7+9-8
=-6
(2) 93.7%
8x2÷4x
=2x
(3) 77.6%
加減法がいいかな?
2つの式を足すとyが消えて、x=-3
これをいずれかに代入して、y=-7
(4) 80.0%
4/√2+√18
=2√2+3√2
=5√2
(5) 50.9%
球の表面積⇒4πr2
4π×(1/3)2=4/9πrcm2
(6) 66.3%
n角形の内角の和⇒180(n-2)
180(5-2)÷5=108°
n角形の外角の和⇒360°
180-360÷5=108°
《正五角形の内角の1つは108°》を暗記していた生徒も多かったと思う。
(7) 70.7%
反比例y=a/x
a=-4×5=-20
y=-20/x
(8) 53.7%
すべての場合⇒結果は裏か表の2通りで硬貨は3枚だから、23=8通り
表1枚、裏2枚⇒硬貨3枚のうち、表となる1枚を選ぶと3通り
確率は3/8
大問2(小問集合)
(1) 50.6%
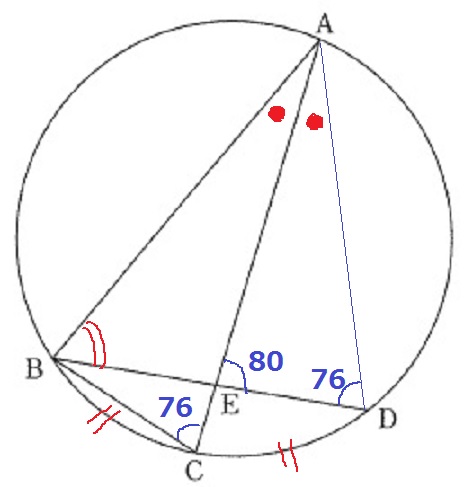
ADに補助線。
弧ABに対する円周角から、∠ADB=76°
△AEDの内角で、∠DAE(●)=180-(80+76)=24°
弧BC=弧CDだから、∠CAB(●)=24°
△ABEで外角定理。
∠ABE=80-24=56°
(2) 30.0%!(無答25.3%)
Bのx座標が1。ここから座標を調べる。
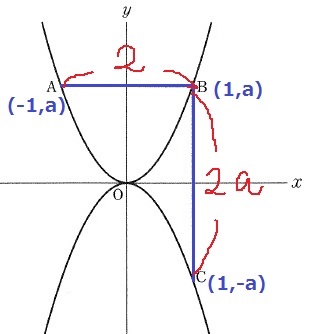
2+2a=16/3
a=5/3
(3) 36.5%
記録をがんばって昇順になおすと・・
〔29・30・31・31・32・35・36・48・52〕
9人の中央値(メジアン)は、(9+1)÷2=5番目の人の記録⇒32kg
Cを加えると中央値は33kgになった。
10人の中央値は5番目と6番目の平均値。
中央値が33へ上がったということは、Cは33より大きい。
一方で、Cが35を超してしまうと、35とCの平均が中央値だから中央値は35を超す。
Cは33より大きく、35より小さい⇒34kg
(5番目…E32kg、6番目…C34kg、中央値…33kg)
大問3(文章題)
花壇の道幅を求める。学テっぽい。
(1) 20.4%!(部分正答2.2%)

4つの花壇を角によせる。
(6-x)(9-x)=40
x2-15x+14=0
(x-1)(x-14)=0
x=1、14
x<6より、x=1
道幅は1mとなる。
ア…15、イ…14、ウ…1
(2)エ…7.6%!! オ…13.3%!(無答-2問とも30%ほど)
後半は√41を小数であらわす。
√36(6)<√41<√49(7)
√41の整数部分は6
小数第1位も同じことをする。(以下、公式解答より)
6.42=40.96、6.52=42.25
6.42<41<6.52
ここから、6.4<√41<6.5
√41の小数第1位は4となる。
エ…4
7-√41において、√41を6.4として計算する。
7-6.4=0.6m
オ…0.6m
大問4(平面図形)
(1) 17.5%!(部分正答28.0%、無答18.1%)
四角形EDCFが平行四辺形である理由。
平行四辺形になるための5つの条件いえるかな?
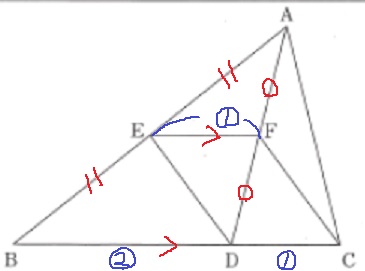
証明の出発点はEがABの中点、FがADの中点。
△ABDで中点連結定理。
EF//BD、EF=1/2BD
EF=DC=①、EF//DCとなり、
1組の対辺が平行で、かつ長さが等しいから四角形EDCFは平行四辺形。
(2) 15.2%!
完全解答。難しい。
頂点の位置を移動させたとき、どこで平行四辺形がひし形になるかを見極める。
Aの位置を固定する。
EはABの中点なので、Bが決まればEの位置が自動的に決まる。
DはBCを2:1に内分する点なので、BとCの位置が決まればDの位置も決まる。
FはADの中点なので、同様にBとCの位置が決まればFも決まる。
ということは、BとCの長さが決まれば全ての位置関係が決まる。
(しかし、B・Cからではなく、はじめに菱形から作った方が綺麗な図になりやすい。
前述の流れは逆からはじめても作図はできるので、
先に菱形の頂点E・D・C・Fの位置を定め、A・Bの順で位置を確定していった方が良い)

5つの選択肢は、AからB・C・D・E・Fからの距離。
なんとなくAC=AEではないかな?と推測する。
ADを対称の軸としたとき、△AEDと△ACDが左右対称で合同、であったら嬉しい…。
もし合同であればED=CDとなり、平行四辺形EDCFで隣り合う辺の長さが等しくなるので、
4辺の長さが等しく、四角形EDCFがひし形と言える。
この証明ですが、けっこう迷いました(´゚д゚`)
どこかで角度が等しい点に言及しなければならないので、
AC=AEを前提に、以下、辺の比をヒントに書きました。
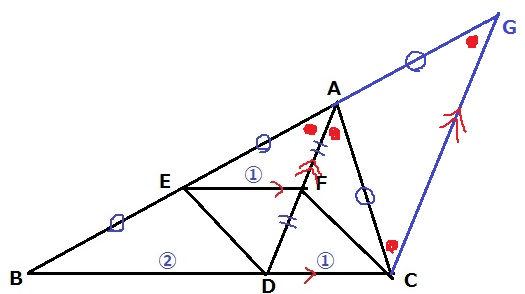
ADに平行な線をCからひき、BAの延長線との交点をGとする。
AD//GCより、△ABD∽GBC
BD:DC=BA:AG=2:1…①
△ABCの辺で、BA:AC=2:1…②
①・②から、AC=AGとなる。
△ACGは二等辺三角形。
∠DAC=∠ACG(錯角)
∠ACG=∠AGC(二等辺の底角)
∠AGC=∠BAD(同位角)
したがって、∠BAD=∠DACとなり、ADは∠BACの二等分線になる。
ここから、△AED≡△ACDや、ADを対称の軸とした対称関係を指摘できるようになり、
ED=DC→平行四辺形の隣り合う辺が同じ長さ→4辺が等しい菱形
もしくは、CとEが対応する点なので、CEとADは垂直に交わる
→対角線ECとFDが直交する→菱形
ア…②、イ…④
@余談@
うえの解説は高校数学(数A)で習う、角の二等分線の定理の逆を利用しました。

頂角の二等分線は、a:b=c:d
a:b=c:dならば、頂角を二等分する(逆)
本問では、AB:AC=BD:DC=2:1と辺の比が共通しています。
大問5(平面図形2)
16.6%!(部分正答15.4%、無答22.4%)
解答欄には過程も記述する。
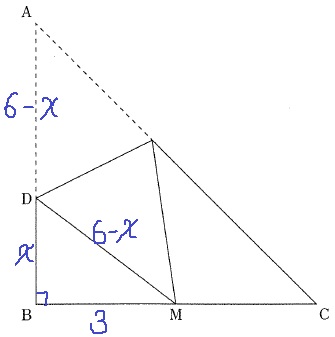
BDをxとおく。
折り返しからDA=DMとわかれば、あとは素直に三平方。
(6-x)2=x2+3
12x=27
x=9/4
BD=9/4cm
大問6(関数)
(1) 73.2%
②がy=-2/3x+4で、Bはこの切片だから4
(2) 1.3%!!!(無答26.4%)
問題文の意味を理解する。
『x座標とy座標がともに整数である点』とは、いわゆる格子点。
①を傾けたとき、OA上の格子点が原点以外で1つしかないところを探す。

aの値は最も小さくするので、x軸方向に接近するように傾ける。
②y=-2/3x+4とx軸との交点は、
0=-2/3x+4
x=6
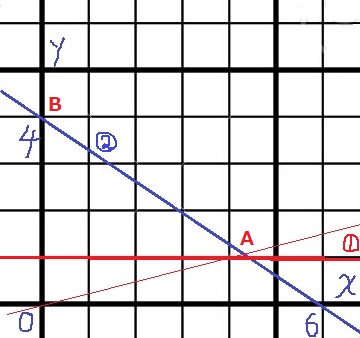
狙うべきは、y=1(赤線)
理由は、①の傾きを0から徐々に上へあげていくと、
OA上の格子点はy=1で作られ始めるから。
①と②の交点のy座標は1以上でなくてはならない。
①が(6、1)を通ると、②とx軸の交点が(6、0)だからOA上に格子点ができない。
①が(5、1)を通ると、②y=-2/3x+4のxに5を代入して、
y=-2/3×5+4=2/3となり、交点のy座標が1未満だから格子点ができない。
①が(4、1)を通ると、y=-2/3×4+4=4/3で、1以上となる。
OAは(4、1)を通り、傾きa=1/4



コメント