2021年度　岡山県公立高校入試問題過去問【数学】解説

平均点は60点付近だそうです。
問題はコチラ→ＰＤＦファイル
出題範囲の縮小はなし。

大問１（小問集合）

①　96.5％
－３－（－７）
＝－３＋７＝４

②　99.5％
（－５）×４
＝－20

③　88.5％
３（ａ－２ｂ）－２（ａ＋ｂ）
＝３ａ－６ｂ－２ａ－２ｂ
＝ａ－8ｂ

④　93.0％
10ａｂ²÷（－２ｂ）
＝－５ａｂ

⑤　87.5％
（√７＋√５）（√７－√５）
＝７－５＝２

⑥　85.0％
ｘ²－５ｘ＋１＝０
解の公式を適用して、ｘ＝（５±√21）/２

⑦　69.0％
ａ＜０だと、上に凸のグラフ→（３）ｙ＝－２ｘ²
ａの値が大きくなるとグラフは細くなる→（１）ｙ＝ｘ²（２）ｙ＝１/２ｘ²
エ

⑧　71.5％
全体は６×６＝36通り
和が５以下→（１、１～４）（２、１～３）（３、１～２）（４、１）
４＋３＋２＋１＝10通り
確率は、10/36＝５/18

⑨　45.5％（部分正答25.0％）
答案では求め方も記述する。
△ＡＢＯで三平方→円錐の高さＡＯ＝２√10ｃｍ
３×３×π×２√10÷３＝６√10πｃｍ³

⑩　65.0％（部分正答3.0％）

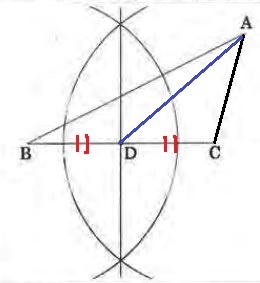
△ＡＢＣを二等分する→ＢＤ＝ＤＣ
ＢＣの垂直二等分線をひき、ＢＣとの交点がＤとなる。

大問２（方程式）

①（１）…75.5％、（２）…59.0％
一次方程式。
全部で50箱。桃がａ箱だから、メロンは50－ａ箱。
桃の売り上げ…750ａ円
メロンの…売り上げ1600（50－ａ）円
売り上げの合計で等式。750ａ＋1600（50－ａ）＝56200
（１）50－ａ、（２）750ａ＋1600（50－ａ）

②（３）…81.5％、（４）…36.5％
連立方程式。
今度は桃の個数をｘ個、メロンの個数をｙ個とおく。
１個１たりの桃の売り上げは、750÷３＝250円
１個あたりのメロンの売り上げは、1600÷２＝800円
売り上げの合計で等式。250ｘ＋800ｙ＝56200

もう１つは箱の合計で等式。
桃の箱…ｘ÷３＝ｘ/３箱
メロンの箱…ｙ÷２＝ｙ/２箱
ｘ/３＋ｙ/２＝50
（３）250ｘ＋800ｙ、（４）ｘ/３＋ｙ/２

③　33.5％（部分正答4.0％）
先の一次方程式か連立方程式を解く。
サボは一次方程式で解きました。
750ａ＋1600（50－ａ）＝56200
750ａ＋80000－1600ａ＝56200
850ａ＝23800
ａ＝28（箱）
桃…28×３＝84個
メロン…（50－28）×２＝44個

大問３（関数）

①　60.0％
反比例はｘとｙの積が比例定数ａで一定。
ア：ｙ＝20/ｘ　〇
イ：ｙ＝６ｘ　比例×
ウ：ｙ＝1000/ｘ　〇
エ：ｙ＝１/３πｘ²　ｙ＝ａｘ²×
ア・ウ

②（１）　85.0％
ａ＝ｘｙ＝４×３＝12

（２）　59.5％
ｙ＝12/ｘに代入。
ｘ＝３のとき、ｙ＝４
ｘ＝８のとき、ｙ＝12/８＝３/２
３/２≦ｙ≦４

③　15.5％！
ｘｙ＝ａ
留意点は反比例は双曲線で、ｘ座標とｙ座標がともに負の場合もあること！
『整数』は負の数を含む。
ａ＝１のとき、ｘｙ＝１→（１、１）（－１、－１）
ａ＝２のとき、ｘｙ＝２→（１、２）（２、１）（－１、－２）（－２、－１）
ａ＝３のとき、ｘｙ＝３→（１、３）（３、１）（－１、－３）（－３、－１）
ａ＝４のとき、ｘｙ＝４→（１、４）（２、２）（４、１）とこれらの負。
ａ＝５のとき、ｘｙ＝５→（１、５）（５、１）とこれらの負。
ａ＝６のとき、ｘｙ＝６→（１、６）（２、３）（３、２）（６、１）とこれらの負。
４つあるのは、ａ＝２、３、５

大問４（データの活用）

①（１）　48.0％
平均値は『2567個』と問題文に書かれてある。
2500～3000個の階級は３回。

（２）　90.5％
最頻値（モード）は最もあらわれている値。
階級は1000個以上1500個未満

（３）　67.5％
先の階級値が最頻値である。
1000と1500の平均である1250個。

②（１）　53.5％（部分正答0.5％）
（300、1000）⇒（500、5000）
右に200、上に4000。傾きは、4000/200＝20
ｙ＝20ｘ＋ｂに（ｘ、ｙ）＝（300、1000）を代入して、
1000＝20×300＋ｂ
ｂ＝－5000
ｙ＝20ｘ－5000

（２）　46.0％
先ほどの式にｘ＝372を代入。
ｙ＝20×372－5000＝2440個

（３）　23.0％！（部分正答11.0％）
中央値は1500個以上2000個未満の階級に含まれ、
2440個はこれよりも大きい値だから、
*度数の合計を数えると31個ある。
30個の中央値は15番目と16番目の平均値→1500個以上2000個未満
答案では中央値ではなく、『中央値が入っている階級』を示すこと。

大問５（平面図形）

①　58.0％（部分正答15.0％）
△ＡＢＤ∽△ＥＣＤの証明。

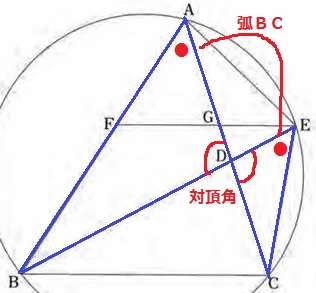
基本の形式なので完全解答を目指したい。
弧ＢＣに対する円周角で∠ＢＡＤ＝∠ＣＥＤ
対頂角で∠ＡＤＢ＝∠ＥＤＣ
２組の角がそれぞれ等しく∽。

②（１）　52.5％

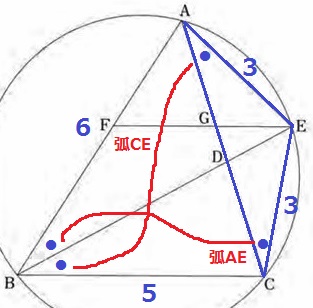
弧ＡＥの円周角より、∠ＡＢＥ＝∠ＡＣＥ
弧ＣＥの円周角より、∠ＥＢＣ＝∠ＥＡＣ
△ＡＣＥは２つの底角が等しいので二等辺三角形。
ＣＥ＝ＡＥ＝３ｃｍ

（２）　35.0％（部分正答0.5％）

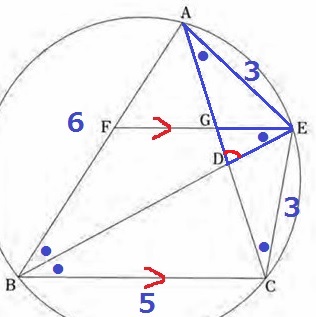
ＥＤ：ＤＧは△ＤＥＧの辺の比である。
そこで、△ＤＥＧと相似関係にある三角形を探す。
２角が等しく、△ＤＥＧ∽△ＤＡＥ。

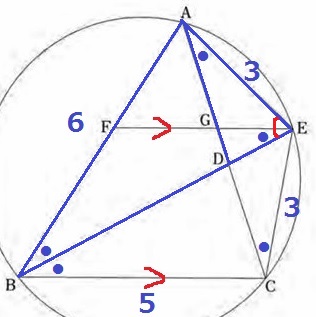
さらに、△ＤＡＥと相似である三角形を探す。
２角相等で△ＤＡＥ∽△ＡＢＥ。

つまり、△ＤＥＧ∽△ＤＡＥ∽△ＡＢＥ。
ＥＤ：ＤＧ＝ＡＤ：ＤＥ＝ＢＡ：ＡＥ＝６：３＝２：１

（３）　1.0％!!!

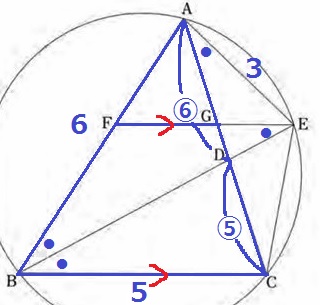
ＡＢ＝６ｃｍがわかっているので、ＡＦ：ＡＢが知りたい。
ＦＧ//ＢＣより、△ＡＦＧ∽△ＡＢＣ。
ＡＦ：ＡＢ＝ＡＤ：ＡＣ
辺ＡＣ上の比に着目する。

角の二等分線の定理より、ＢＡ：ＢＣ＝ＡＤ：ＤＣ＝⑥：⑤
（角の二等分線の定理は他県でも出てくるのでおさえておこう！）

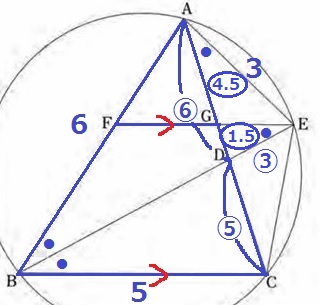
ここで前問のＡＤ：ＤＥ＝ＥＤ：ＤＧ＝２：１を使う。
ＤＥ＝⑥÷２＝③
ＧＤ＝③÷２＝〇1.5
ＡＧ＝⑥－〇1.5＝〇4.5

ＡＧ：ＡＣ＝ＡＦ：ＡＢ＝〇4.5：⑪
ＡＦ＝６×〇4.5/⑪＝27/11ｃｍ
公立高校入試解説ページに戻る