問題ＰＤＦ
①
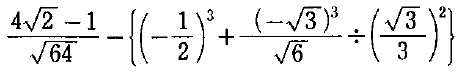を計算すると〔 〕である。
②
半径１ｃｍ、面積１ｃｍ2のおうぎ形の弧の長さは〔 〕ｃｍである。
③
関数ｙ＝ｘ2と関数ｙ＝ａｘ＋ｂ（ａ＜０）について、ｘの変域がともに－２≦ｘ≦１のとき、
ｙの変域が一致する。このときａ＝〔 １ 〕、ｂ＝〔 ２ 〕である。
④
２から６までの整数が１つずつ書かれた５枚のカードがある。このカードをよくきってから１枚ずつ２回続けて取り出し、取り出した順にカードを左から右に並べて２桁の整数を作る。
作られた数をａとするとき√ａが整数となる確率は〔 〕である。
⑤
次の表は、８人の生徒に20点満点の数学の小テストを行い、その結果をまとめたものである。８人の生徒の平均点が12.0点であるとき、生徒番号６の生徒の得点について、ａ2＝〔 １ 〕であり、中央値は＝〔 ２ 〕である。ただし、各生徒の得点はすべて０以上の整数の値であるとする。
⑥
平面上に、１つの直線上にない３点Ｏ、Ａ、Ｂがある。線分ＯＡと線分ＯＢの長さが等しくないとき、次の２つの条件をともに満たす点Ｐを作図する方法を考えたい。
（条件１）点Ｐは、点Ｏを端とする２つの半直線ＯＡ、ＯＢに接する円の中心である。
（条件２）点Ｐは、∠ＰＡＢ＝∠ＰＢＡを満たす。
（条件１）を満たす点は〔 １ 〕上の点であり、（条件２）を満たす点は（ ２ ）上の点であるから、これらの交点がＰである。
〔 １ 〕〔 ２ 〕に当てはまることばとして最も適当なのはどれですか。それぞれ一つ答えなさい。
ア：点Ｏと線分ＡＢの中点を結ぶ直線 イ：∠ＡＯＢの二等分線
ウ：点Ｏを通り直線ＡＢに垂直な直線 エ：点Ｏを通り直線ＡＢに平行な直線
オ：線分ＡＢの垂直二等分線 カ：線分ＡＢを直径とする円周
＠解説＠
①
指数の処理で符号を取り違えないように！最後は８で通分。
５√２
②
中心角を□とおいてしまおう。
□＝１/π
弧の長さは２ｃｍ。
③
ｙ＝ｘ2において－２≦ｘ≦１のとき、
ｘ＝０のとき 最小値ｙ＝０
ｘ＝－２のとき 最大値ｙ＝４
ｙの変域は０≦ｙ≦４
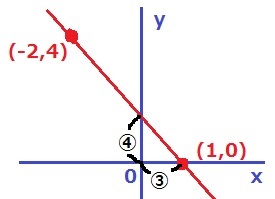
ａ＜０なので、ｙ＝ａｘ＋ｂは右下。
－２≦ｘ≦１のとき、０≦ｙ≦４だから、
ｘ＝－２のとき 最大値ｙ＝４
ｘ＝１のとき 最小値ｙ＝０
（－２、４）（１、０）の点を通過する。
右に３、下に４だから、傾きは－４/３。
切片は、１×④/③＝４/３
（１）－４/３、（２）４/３
④
ａが平方数であれば根号が外れて整数となる。
ａ＝25、36、64
３通り
５枚から連続して２回とるので、５×４＝20通り
確率は３/20。
⑤
８人の合計…12×８＝96点
ａ2＋ａ＝96－（13＋18＋20＋19＋４＋10）
＝96－84＝12
ａ2＋ａ－12
＝（ａ＋４）（ａ－３）＝０
ａ＞０より、ａ＝３
ａ2＝９
８人の中央値は４番目と５番目の平均値。
10と13の平均→11.5点
（１）９、（２）11.5点
⑥
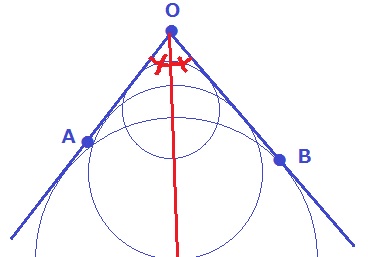
（条件１）半直線ＯＡとＯＢに接する円
→円の中心Ｐは∠ＡＯＢの二等分線上にある。
（条件２）∠ＰＡＢ＝∠ＰＢＡ
→ＡＢの垂直二等分線を対称の軸とすると、対応する角の大きさが等しい。
（１）イ、（２）オ
国私立高校入試解説ページに戻る
コメント