問題PDF
問1
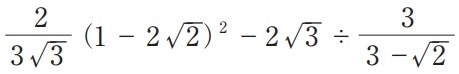 を計算せよ。
を計算せよ。
問3
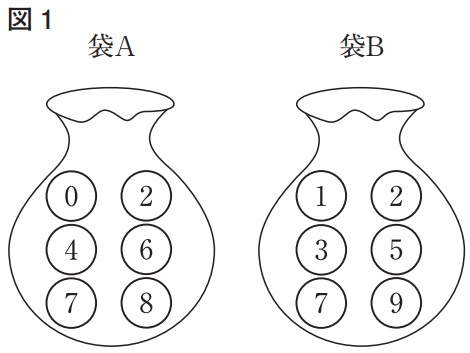
上の図1のように、0、2、4、6、7、8の数が1つずつ書かれた6個のボールが入っている袋Aと、1、2、3、5、7、9の数が1つずつ書かれた6個のボールが入っている袋Bがある。2つの袋A、Bから同時にそれぞれ1個のボールを取り出す。袋Aから取り出されたボールに書かれた数をa、袋Bから取り出されたボールに書かれた数をbとするとき、![]() が有理数となる確率を求めよ。ただし、2つの袋A、Bそれぞれについて、どのボールが取り出されることも同様に確からしいものとする。
が有理数となる確率を求めよ。ただし、2つの袋A、Bそれぞれについて、どのボールが取り出されることも同様に確からしいものとする。
問4
aを整数とする。
次のaを含む8個の整数の中央値をMとする。
a、25、26、27、30、31、32、35
このとき、Mの取り得る値は何通りあるか。
問5

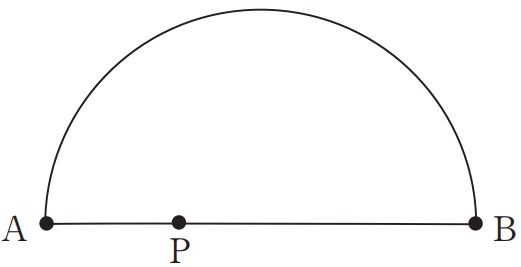
上の図2は、線分AB上の点をPとし、線分ABを直径とする半円を、折り返した弧と線分ABが点Pで接するように1回だけ折り、できた折り目を線分QRとしたものである。
解答欄に示した図をもとにして、線分QRを定規とコンパスを用いて作図せよ。ただし、作図に用いた線は消さないでおくこと。
@解説@
問1

初めてiPadで書いてみたのですが慣れない|-`)…
3√3で通分。分数をつなげるときは符号に注意。
-2√6/9
問2

最初は小数で統一しました。
解の公式はb=2b’を使って、x=(1±√19)/2
問3
ボールの取り出し方は6×6=36通り
![]() が有理数となる組み合わせを探していくが、骨の折れる作業です(;`ω´)
が有理数となる組み合わせを探していくが、骨の折れる作業です(;`ω´)
地道にあてはめていくのが確実だが、36個もパターンがあるので時間との闘いになる。

有理数→根号を外す。
●a=0
aが0だと、√b/√b=1で有理数。
袋Bは何でもよいので6通り
●aとbが同数
同数の場合、√b/2√b=1/2で有理数。
(a、b)=(2、2)(7、7)
●0以外の平方数
平方数であれば根号が外れて有理数になる。
a=4しかない。b=1、9
●〇√〇に変換して根号の中が同数
もう1つが曲者。
√8=2√2と変換すれば、根号の中が全て2となり、
同数のパターンと同様に有理数になる。
*√2/(2√2+√2)=1/3
(a、b)=(8、2)
計11通り、確率は11/36
問4
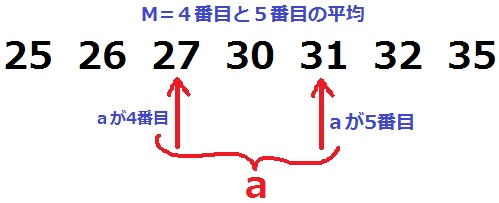
8個の中央値Mは4番目と5番目の平均値。
aが4番目になるのは27から。(25・26・27・27)
aが5番目になるのは31まで。(25・26・27・30・31・31)
27~31の5通り
問5
この作図はなかなかの難度です。

折り返しなのでQRを対称の軸とすると、Pに対応するP’は弧AB上のどこかにある。
PP’の垂直二等分線がQRなので、P’を作ろうとしたいが・・
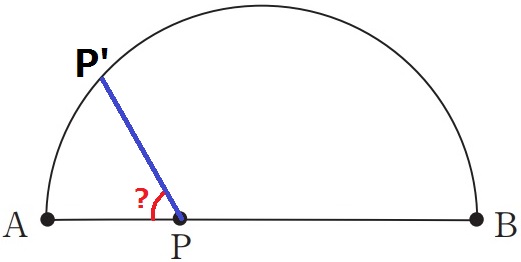
解答用紙の図ではP’の位置が特定できない!
QRのためにP’を探りたいが、P’を特定にするにはQRが必要という板バサミ。
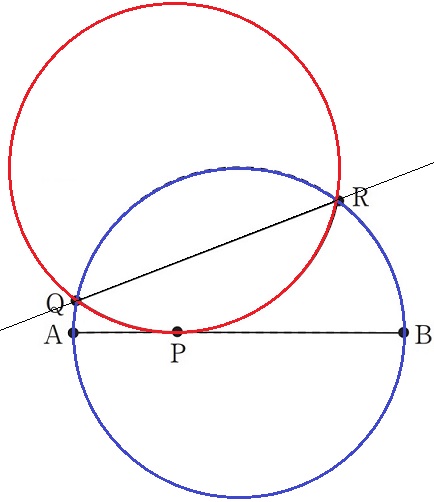
そこで別の方向から攻めてみる。半円を円にしてみよう。
P以外で折り返せるものといえば円。
QRを対称の軸として左上に円を作成する。
赤い円(弧QR)⇒弦QRの順に描いていく。
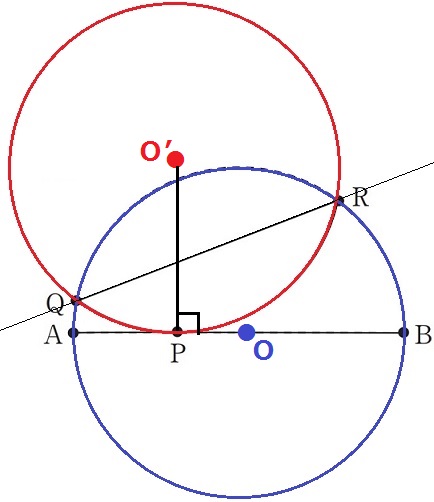
青い円の中心OはABの垂直二等分線で決まる。
赤い円の中心O’はどうするか?
『折り返した弧と線分ABが点Pで接する』
円O’は接線ABと接点Pで接している。
半径と接線の関係は垂直だからO’P⊥AB
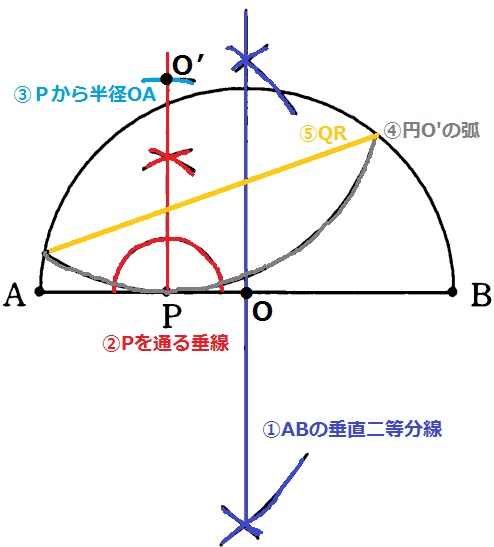
①ABの垂直二等分線。中心Oがでる。
②Pを通る垂線。垂線上にO’がある。
③2つの円の半径は同じ。半径AOの長さをとってPから長さを移す。中心O’がでる。
④弧ABと2点が交わるように、O’からグルっと弧を描く。
⑤2つの交点QRを結ぶ。


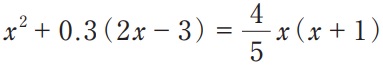

コメント