2021年度　久留米大学附設高校過去問【数学】大問１解説

問題ＰＤＦ
（１）
連立方程式

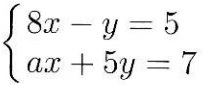
の解をｘ＝ｍ、ｙ＝ｎとするとき、２ｍ－ｎ＝１が成り立つ。
このとき、ａの値を求めよ。

（２）
２次方程式ｘ²＋ｘ－１＝０の大きい方の解をａ、小さい方の解をｂとする。
このとき、の値を求めよ。

（３）
２つの文字ａ、ｂを左から何文字か並べる。
ただし、同じ文字を何回使ってもよいが、ａの次は必ずｂを並べ、
ｂの次はどちらの文字を並べてもよいものとする。
例えば、３文字を並べるとき、ａｂａ、ａｂｂ、ｂａｂ、ｂｂａ、ｂｂｂ
の５通りの並べ方がある。
５文字を並べるとき、何通りの並べ方があるか。

（４）
１つのさいころを３回投げるとき、
出た目の最大値が３で最小値が１になる確率を求めよ。

（５）

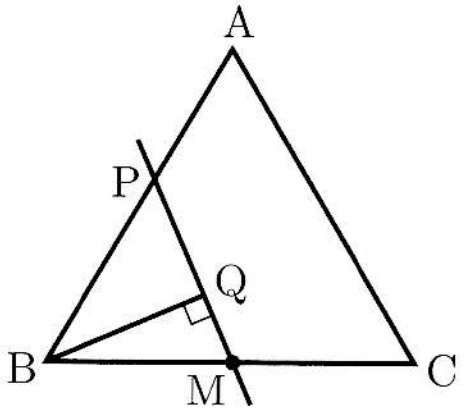
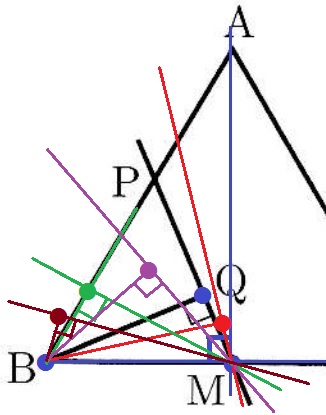
図のように、１辺の長さが４の正三角形ＡＢＣがあり、辺ＢＣの中点をＭとする。
辺ＡＢ上を動く点をＰとし、Ｂから直線ＰＭに垂線ＢＱを引く。
ただし、点ＰがＢと一致するときは点ＱがＢと一致することにする。
ＰがＡからＢまで動くとき、線分ＢＱが通過した部分で、
正三角形ＡＢＣＤの内部にある部分の面積を求めよ。

＠解説＠
（１）

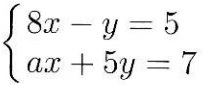
『この解をｘ＝ｍ、ｙ＝ｎとするとき、２ｍ－ｎ＝１が成り立つ』
ｘをｍ、ｙをｎに変換する。

８ｍ－ｎ＝５　…①
ａｍ＋５ｎ＝７　…②
２ｍ－ｎ＝１　…③

①と③で連立を組む。
ｍ＝２/３、ｎ＝１/３

②に放り込む。
２/３ａ＋５/３＝７
ａ＝８

（２）
ｘ²＋ｘ－１＝０
解の公式を適用して、ａ＝（－１＋√５）/２、ｂ＝（－１－√５）/２

解の和と積の形にしてから代入を試みる。
ａ＋ｂ＝（－１＋√５－１－√５）/２＝－１

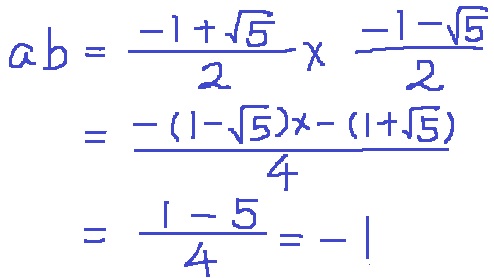
↑マイナスでくくって和と差の積にしている。

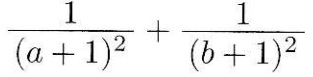
これをどうにかしてａ＋ｂ、ａｂの形にしたいが難しい(;´･ω･)

ｘ²＋ｘ－１＝０
（ａ＋１）²や（ｂ＋１）²のように（ｘ＋１）²＝〇に変えられないものか？
ｘ²＋ｘ－１＝０
ｘ²＝－ｘ＋１

（ｘ＋１）²
＝ｘ²＋２ｘ＋１　←先のｘ²＝－ｘ＋１を代入
＝（－ｘ＋１）＋２ｘ＋１
＝ｘ＋２

ｘの解であるａ、ｂにも同じ形を適用。
（ａ＋１）²＝ａ＋２
（ｂ＋１）²＝ｂ＋２

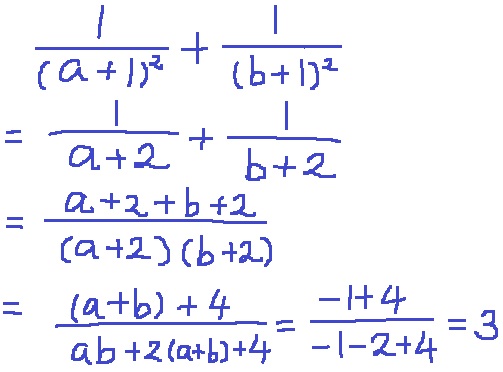
（３）
条件のないｂの数で場合分けする。
◆ｂが０個
例題ではｂｂｂもカウントしている。１通り。

◆ｂが１個
例題にｂｂａがあるので、ａは右端でもＯＫ。
ｂはどこでも良いから５通り。

◆ｂが２個

ａの次にａを置かない。６通り

◆ｂが３個

これしかない１通り。
合計して13通り。

＠別解＠
某フォロワーさんより、算数によくある漸化式ぜんかしきという気になるワードを耳にし、
あれこれ考えてみました。
◆１文字の場合
ａ、ｂの２通り
◆２文字の場合
ａｂ、ｂａ、ｂｂの３通り
◆３文字
問題文より５通り・・

【２、３、５…】とくればフィボナッチじゃありませんかッ！
４文字なら３＋５＝８通り
５文字なら５＋８＝13通り
６文字なら８＋13＝21通りです。

なぜ、フィボナッチになるのかという点ですが、

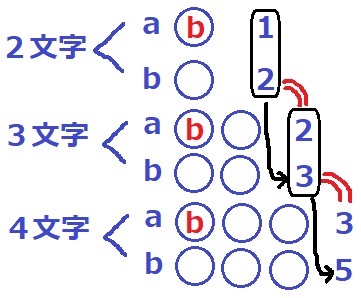
左端がｂの場合、１個前のａとｂの合計と同じになる。
たとえば、４文字のｂだと右側の【〇〇〇】は３文字の５通りである。
また、左端がａの場合、１個前のｂと同じになる。
たとえば、４文字のａだと右側は【ｂ〇〇】の並びとなり、
３文字の【ｂ〇〇】の３通りと等しく、これは２文字の３通りである。
このように、１個前の項（左端ｂ）と２個前の項（左端ａ）の和が連なる数列となる。

（４）
『最小値１、最大値３』ということは、１と３は必ず出す。
残り１つは１～３のどれか。
（１、１、３）⇒３通り
（１、２、３）⇒６通り
（１、３、３）⇒３通り
合計12通り。
確率は、12÷（６×６×６）＝１/18

（５）
図形の移動は附設で狙われている。（2020年度久留米大学付設高校大問４）

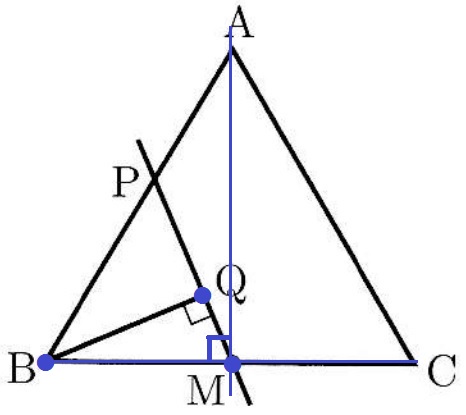
ＰがＡにあるとき、ＡＭ⊥ＢＣよりＱはＭと重なる。
３つの●をＱは通過する。

いっぱい増やしてみました。なんとなく半円に見える。

∠ＢＱＭ＝90°が維持されることから、円周角の定理を想起する。
∠ＢＱＭは半円の弧に対する円周角、
すなわち、点Ｑの軌跡は直径をＢＭとする円の円周（半円）である。

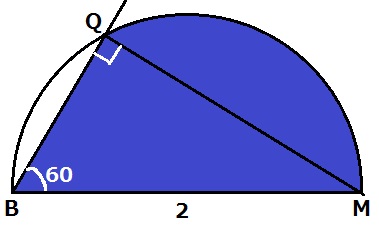
ＱがＡＢ上にくる状態を描いて、求積すべき範囲を確定する。

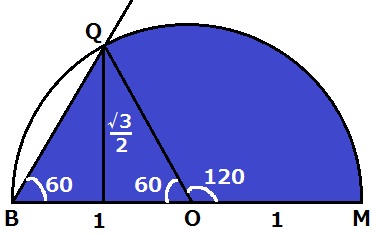
半円の中心をＯとしてＯＱを結ぶ。
半径１ｃｍ・中心角120°の扇形と、１辺１ｃｍの正三角形を足せばいい。
１×１×π×１/３＋１×√３/２×１/２
＝π/３＋√３/４ｃｍ²
国私立高校入試解説ページに戻る